Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Звезды
Содержание
- 1. Звезды
- 2. Задачи исследования1. Определение и классификация звездчатых многоугольников
- 3. Назовём n-конечной звездой нулевого порядка выпуклый n-угольник.
- 4. Пусть А1, А2, …,
- 5. Теорема 1: Количество
- 6. Теорема 2: Сумма углов звездочки k-порядка равна
- 7. Введем следующее определение:Пусть отрезки АD и ВС
- 8. Слайд 8
- 9. Теорема 3: Сумма
- 10. Доказательство теоремы 3 при k=2 Доказательство аналогично
- 11. О расположение вершин n-конечных
- 12. Слайд 12
- 13. Нетрудно видеть, что отрезки, образующие пятиконечную звезду
- 14. ВыводыВ отношении суммы углов n-конечные звезды к-го
- 15. Использованные ресурсыДля выполнения чертежей использована программа «Geogebra»
- 16. Работу выполнила Бабич Ангелина Игоревна, учащаяся 7
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ЗВЁЗДЫ
«Звездочки ясные, звезды высокие!
Что вы храните в себе, что
скрываете? Звезды, таящие мысли глубокие, Силой какою вы душу пленяете?»
ЕсенинСлайд 2Задачи исследования
1. Определение и классификация звездчатых многоугольников (звезд).
2. Вывести
свойства n - конечных звезд
а) Количество
вершин звезды к-го порядка. б) Сумма углов (2k+3)-конечной звезды k-го порядка.
в) Сумма углов n - конечной звезды к-го порядка
г) Расположение вершин n - конечных звезд
Вывести свойства правильных n-конечных звезд
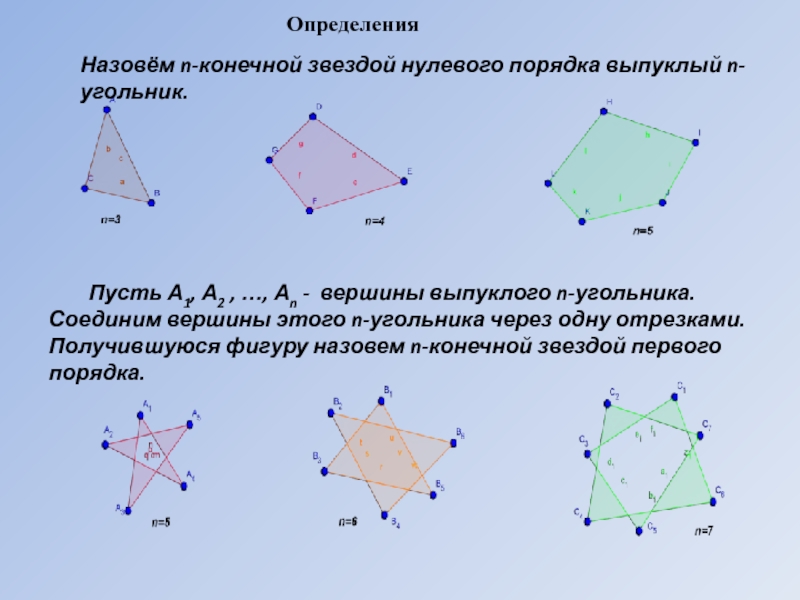
Слайд 3Назовём n-конечной звездой нулевого порядка выпуклый n-угольник.
Пусть А1, А2 , …, Аn - вершины выпуклого n-угольника.
Соединим вершины этого n-угольника через одну отрезками. Получившуюся фигуру назовем n-конечной звездой первого порядка.Определения
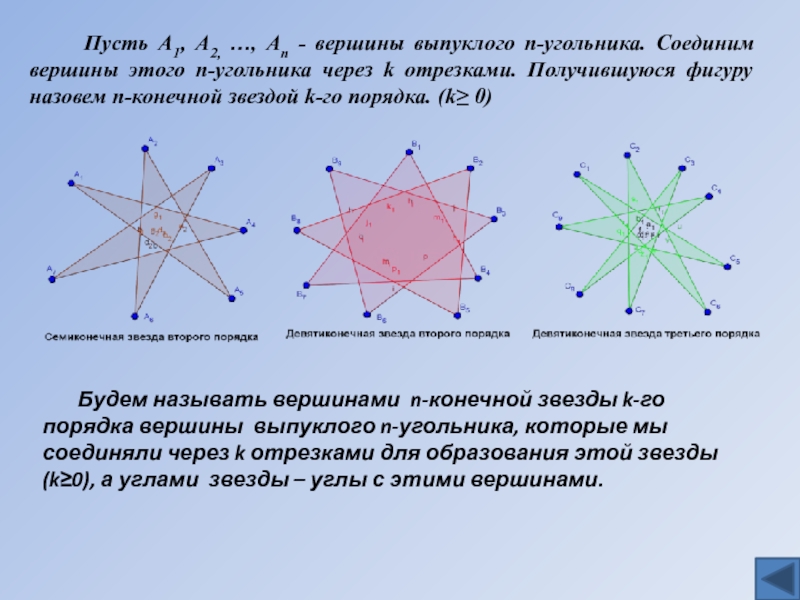
Слайд 4 Пусть А1, А2, …, Аn - вершины
выпуклого n-угольника. Соединим вершины этого n-угольника через k отрезками. Получившуюся
фигуру назовем n-конечной звездой k-го порядка. (k≥ 0) Будем называть вершинами n-конечной звезды k-го порядка вершины выпуклого n-угольника, которые мы соединяли через k отрезками для образования этой звезды (k≥0), а углами звезды – углы с этими вершинами.
Слайд 5Теорема 1: Количество вершин звезды к-го
порядка
не менее 2к + З, где k≥0.Доказательство:
Пусть А – некоторая вершина звезды к-го порядка. Она соединена ровно с двумя вершинами, обозначим их В и С. По ту сторону от прямой АВ, где не лежит вершина С, находится ровно к вершин звезды.
По ту сторону от прямой АС, где не лежит точка В,
находится ровно к вершин звезды.
Значит количество вершин звезды не менее 2к +3,
что и требовалось доказать.
Если между вершинами В и С не лежит ни одной вершины, то количество вершин звезды равно 2к +3.
Таким образом, 2к +3 – наименьшее количество вершин n-конечной звезды к-го порядка.
Будем называть (2к +3) - конечные звезды к-го порядка «звездочками» к-го порядка.
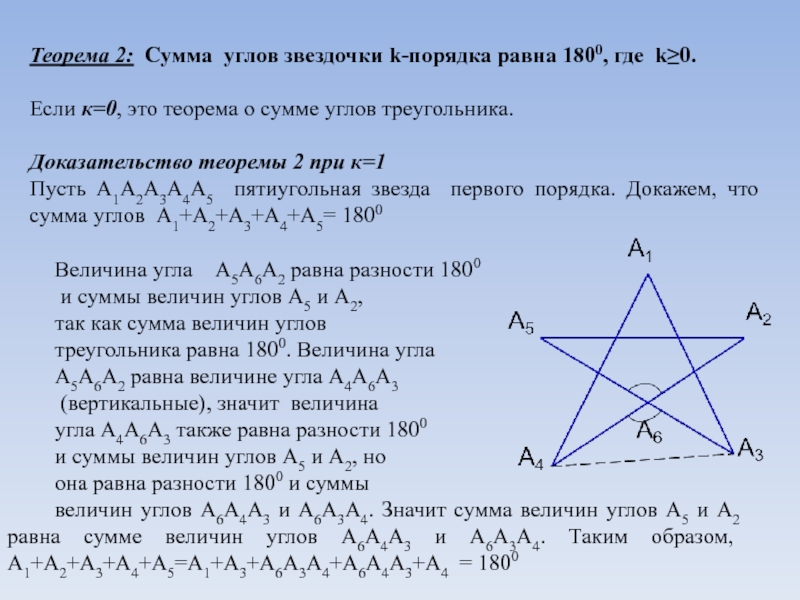
Слайд 6Теорема 2: Сумма углов звездочки k-порядка равна 1800, где k≥0.
Если
к=0, это теорема о сумме углов треугольника.
Доказательство теоремы 2 при
к=1 Пусть А1А2А3А4А5 пятиугольная звезда первого порядка. Докажем, что сумма углов А1+А2+А3+А4+А5= 1800
Величина угла А5А6А2 равна разности 1800
и суммы величин углов А5 и А2,
так как сумма величин углов
треугольника равна 1800. Величина угла
А5А6А2 равна величине угла А4А6А3
(вертикальные), значит величина
угла А4А6А3 также равна разности 1800
и суммы величин углов А5 и А2, но
она равна разности 1800 и суммы
величин углов А6А4А3 и А6А3А4. Значит сумма величин углов А5 и А2 равна сумме величин углов А6А4А3 и А6А3А4. Таким образом, А1+А2+А3+А4+А5=А1+А3+А6А3А4+А6А4А3+А4 = 1800
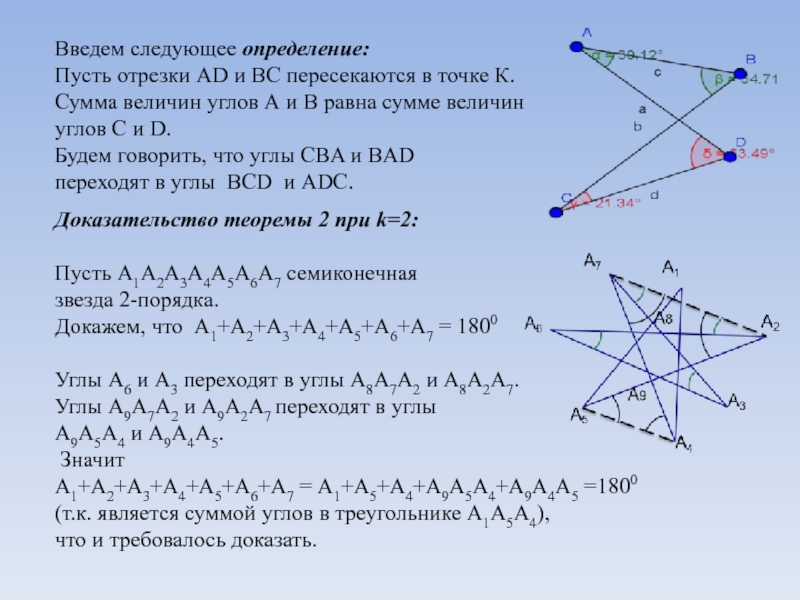
Слайд 7Введем следующее определение:
Пусть отрезки АD и ВС пересекаются в точке
К.
Сумма величин углов А и В равна сумме величин
углов С и D.
Будем говорить, что углы CВA и ВAD
переходят в углы BСD и ADС.
Доказательство теоремы 2 при k=2:
Пусть А1А2А3А4А5А6А7 семиконечная
звезда 2-порядка.
Докажем, что А1+А2+А3+А4+А5+А6+А7 = 1800
Углы А6 и А3 переходят в углы А8А7А2 и А8А2А7.
Углы А9А7А2 и А9А2А7 переходят в углы
А9А5А4 и А9А4А5.
Значит
А1+А2+А3+А4+А5+А6+А7 = А1+А5+А4+А9А5А4+А9А4А5 =1800
(т.к. является суммой углов в треугольнике А1А5А4),
что и требовалось доказать.
Слайд 8
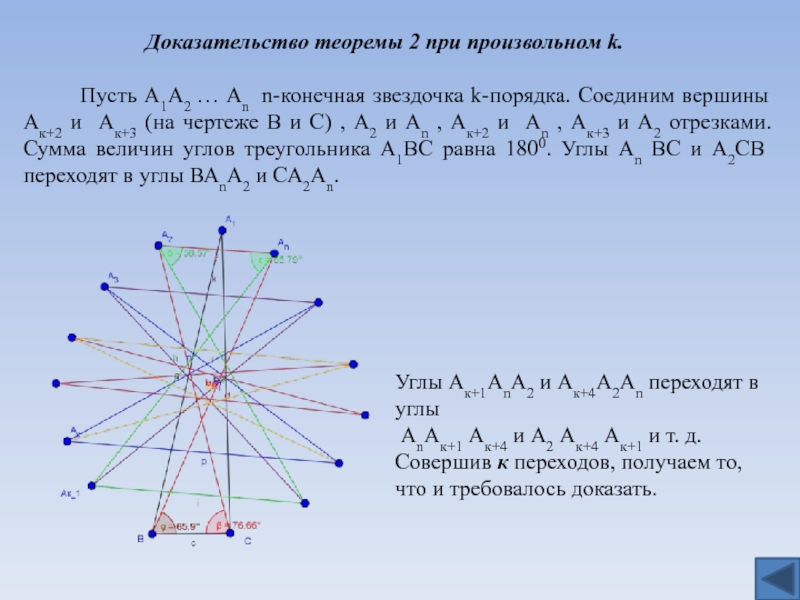
Доказательство теоремы 2 при произвольном k.
Пусть А1А2 … Аn n-конечная звездочка k-порядка. Соединим вершины Ак+2 и Ак+3 (на чертеже В и С) , А2 и Аn , Ак+2 и Аn , Ак+3 и А2 отрезками. Сумма величин углов треугольника А1ВС равна 1800. Углы Аn ВС и А2СВ переходят в углы ВАnА2 и СА2Аn.Углы Ак+1АnА2 и Ак+4А2Аn переходят в углы
АnАк+1 Ак+4 и А2 Ак+4 Ак+1 и т. д.
Совершив к переходов, получаем то,
что и требовалось доказать.
Слайд 9Теорема 3:
Сумма углов n-конечной звезды
к-го порядка равна 180˚(n – (2к+2))
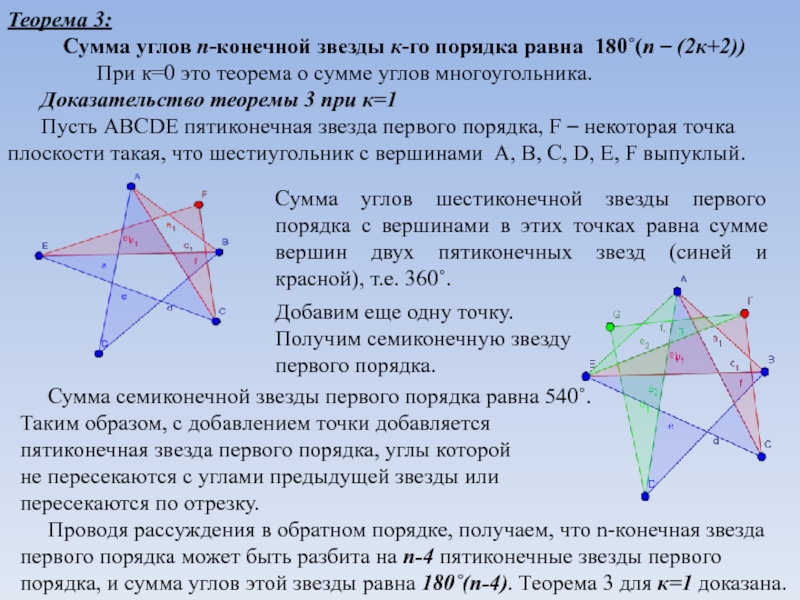
При к=0 это теорема о сумме углов многоугольника.Доказательство теоремы 3 при к=1
Пусть АВСDE пятиконечная звезда первого порядка, F – некоторая точка плоскости такая, что шестиугольник с вершинами А, В, С, D, E, F выпуклый.
Сумма углов шестиконечной звезды первого порядка с вершинами в этих точках равна сумме вершин двух пятиконечных звезд (синей и красной), т.е. 360˚.
Добавим еще одну точку.
Получим семиконечную звезду
первого порядка.
Сумма семиконечной звезды первого порядка равна 540˚.
Таким образом, с добавлением точки добавляется
пятиконечная звезда первого порядка, углы которой
не пересекаются с углами предыдущей звезды или
пересекаются по отрезку.
Проводя рассуждения в обратном порядке, получаем, что n-конечная звезда
первого порядка может быть разбита на n-4 пятиконечные звезды первого
порядка, и сумма углов этой звезды равна 180˚(n-4). Теорема 3 для к=1 доказана.
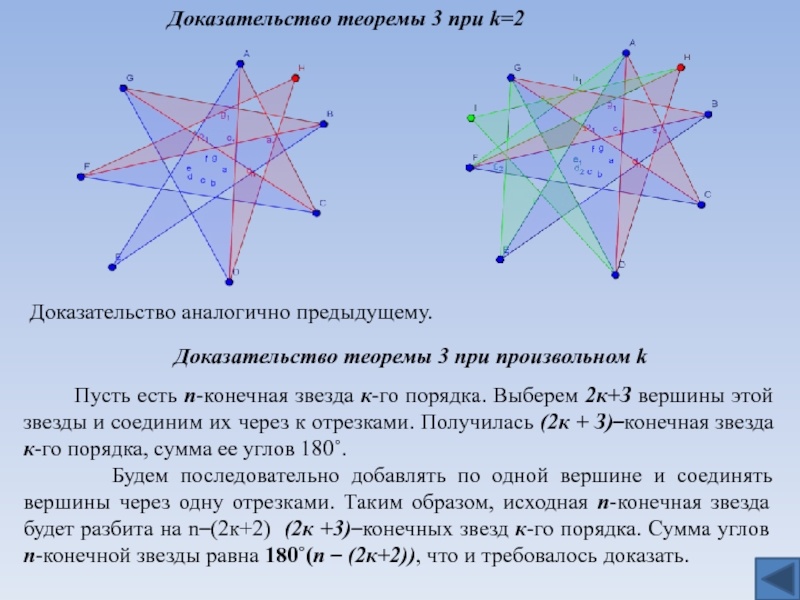
Слайд 10Доказательство теоремы 3 при k=2
Доказательство аналогично предыдущему.
Доказательство теоремы 3
при произвольном k
Пусть есть n-конечная звезда
к-го порядка. Выберем 2к+З вершины этой звезды и соединим их через к отрезками. Получилась (2к + З)–конечная звезда к-го порядка, сумма ее углов 180˚. Будем последовательно добавлять по одной вершине и соединять вершины через одну отрезками. Таким образом, исходная n-конечная звезда будет разбита на n–(2к+2) (2к +3)–конечных звезд к-го порядка. Сумма углов n-конечной звезды равна 180˚(n – (2к+2)), что и требовалось доказать.
Слайд 11 О расположение вершин n-конечных звезд
Давая определение n-конечной
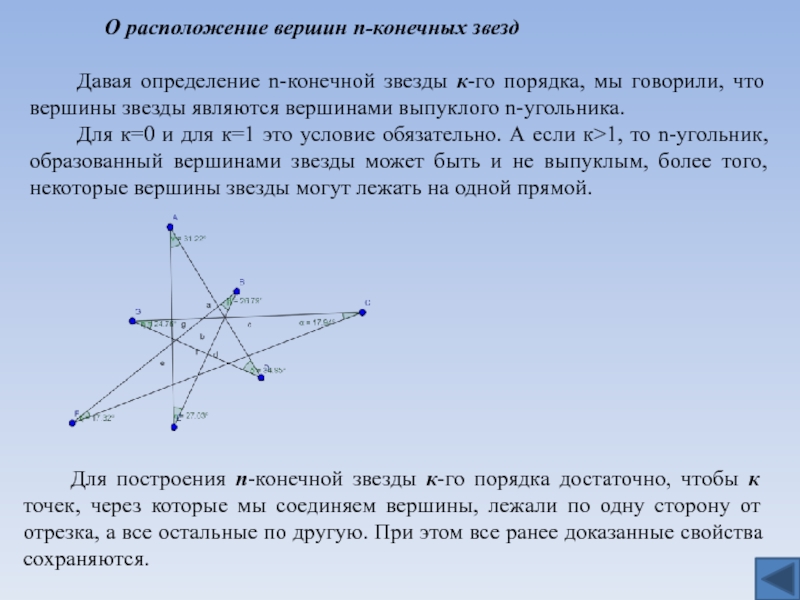
звезды к-го порядка, мы говорили, что вершины звезды являются вершинами
выпуклого n-угольника.Для к=0 и для к=1 это условие обязательно. А если к>1, то n-угольник, образованный вершинами звезды может быть и не выпуклым, более того, некоторые вершины звезды могут лежать на одной прямой.
Для построения n-конечной звезды к-го порядка достаточно, чтобы к точек, через которые мы соединяем вершины, лежали по одну сторону от отрезка, а все остальные по другую. При этом все ранее доказанные свойства сохраняются.
Слайд 12 §3.
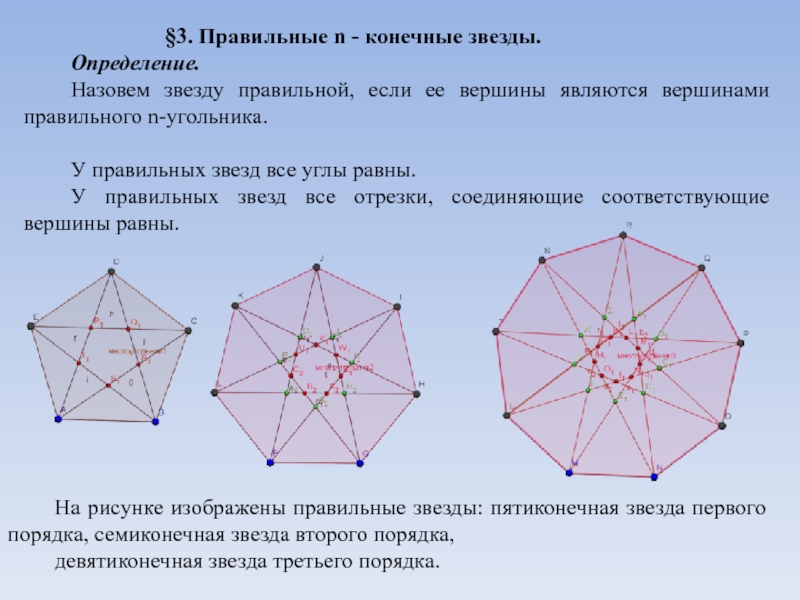
Правильные n - конечные звезды.
Определение.
Назовем звезду правильной, если ее вершины
являются вершинами правильного n-угольника.У правильных звезд все углы равны.
У правильных звезд все отрезки, соединяющие соответствующие вершины равны.
На рисунке изображены правильные звезды: пятиконечная звезда первого порядка, семиконечная звезда второго порядка,
девятиконечная звезда третьего порядка.
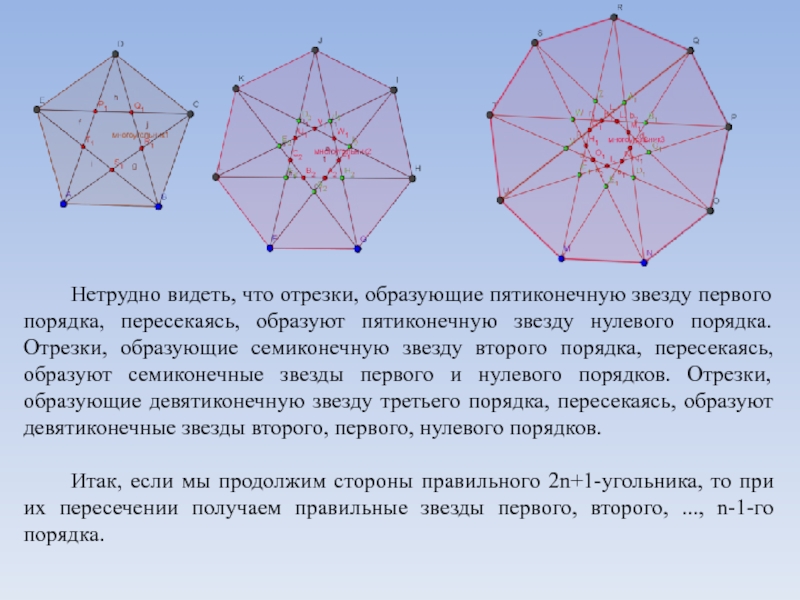
Слайд 13Нетрудно видеть, что отрезки, образующие пятиконечную звезду первого порядка, пересекаясь,
образуют пятиконечную звезду нулевого порядка. Отрезки, образующие семиконечную звезду второго
порядка, пересекаясь, образуют семиконечные звезды первого и нулевого порядков. Отрезки, образующие девятиконечную звезду третьего порядка, пересекаясь, образуют девятиконечные звезды второго, первого, нулевого порядков.Итак, если мы продолжим стороны правильного 2n+1-угольника, то при их пересечении получаем правильные звезды первого, второго, ..., n-1-го порядка.
Слайд 14Выводы
В отношении суммы углов n-конечные звезды к-го порядка ведут себя
так же, как и выпуклые n-угольники.
n-конечная звезда к-го порядка может
быть разбита на n–(2к+2)(2к +3)-конечных звезд к-го порядка.
Правильные n-конечные звезды обладают некоторыми свойствами правильных многоугольников.
При продолжении сторон правильного 2n+1-угольника в их пересечении получаются правильные звезды первого, второго, ..., n-1-го порядка.
Слайд 15Использованные ресурсы
Для выполнения чертежей использована программа «Geogebra»
Для выполнения презентации
Программа «Power Point»
Программа «Geogebra»
При
подготовке доклада литературой и другими источниками не пользовалась.Слайд 16Работу выполнила Бабич Ангелина Игоревна,
учащаяся 7 класса
МАОУ ДО
«Компьютерный центр»
Научный руководитель Рысева Людмила Николаевна,
педагог дополнительного образования
МАОУ ДО «Компьютерный центр»