Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
03
Содержание
- 1. 03
- 2. ЛогикаЛОГИКАКомбинаторнаяПоследовательностнаяПреобразование кодовЛогика с памятью
- 3. Преобразование кодовТаблица истинностиОригинальная часть.ВыходыСтандартная часть.Входы2n строк
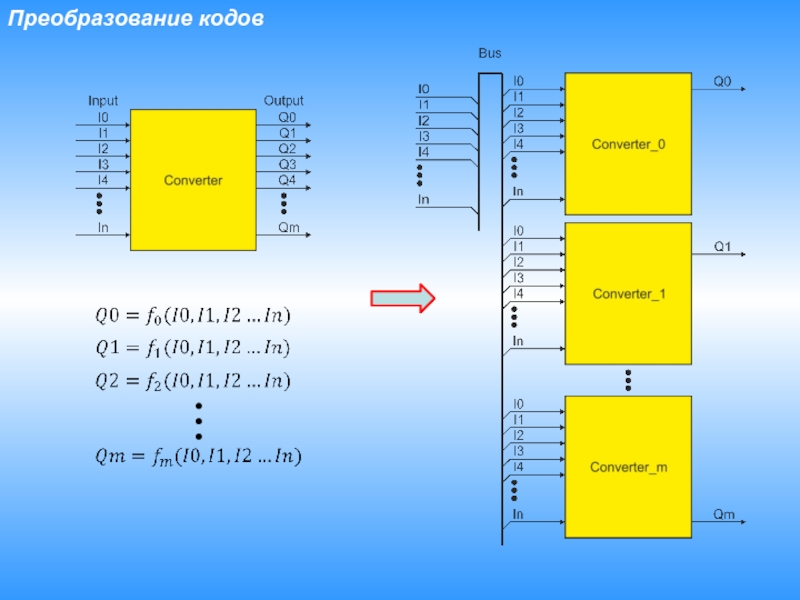
- 4. Преобразование кодов
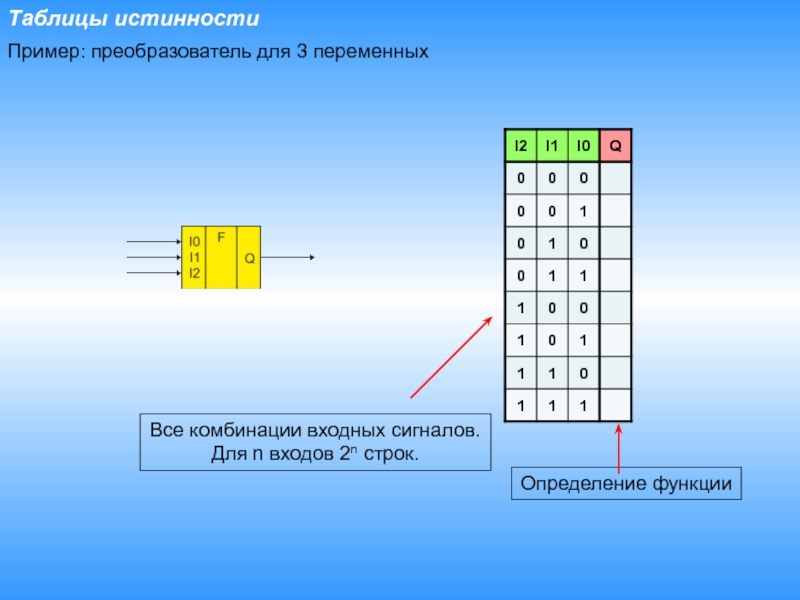
- 5. Таблицы истинностиВсе комбинации входных сигналов.Для n входов 2n строк.Определение функцииПример: преобразователь для 3 переменных
- 6. Функции одной переменнойРисунок из книги
- 7. Логические функции одной переменнойБуферИнверторДругое обозначениеДругое обозначениеДругое обозначение
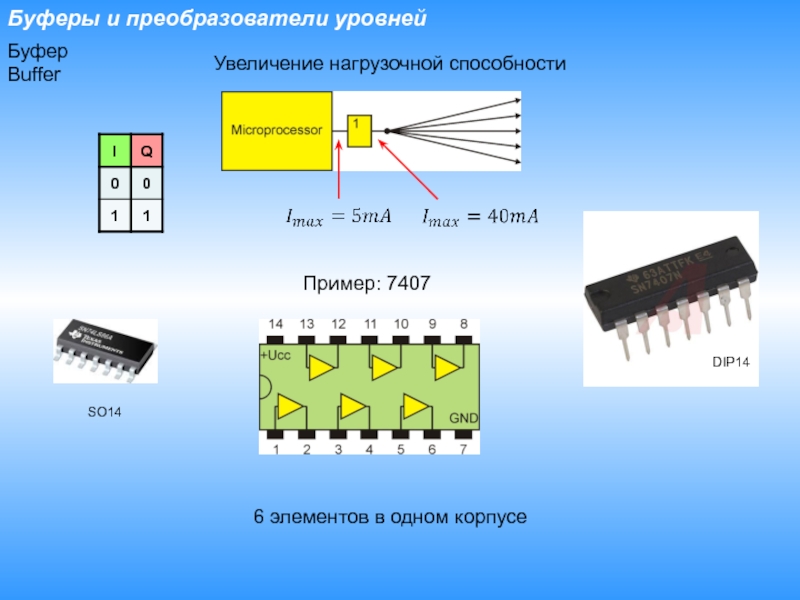
- 8. Буферы и преобразователи уровнейБуферBufferУвеличение нагрузочной способностиПример: 74076 элементов в одном корпусеDIP14SO14
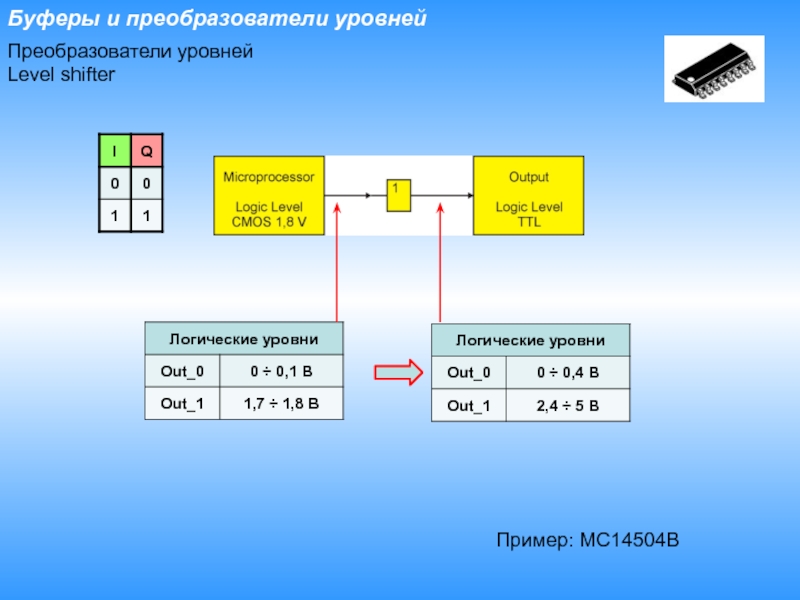
- 9. Буферы и преобразователи уровнейПреобразователи уровнейLevel shifterПример: MC14504B
- 10. ИнверторЕдинственная нетривиальная логическая функция от одной переменнойилиТаблица истинности (определение функции)Графическое обозначениеСимвол отрицания Алгебраическое обозначениеШтрих ШеффераNOT
- 11. Функции двух переменныхВсего 24=16 функций.Нетривиальных и симметричных → 6.2AND2NAND2OR2NORXORNXOR4
- 12. Логическое умножение (конъюнкция)ГрафическоеобозначениеАлгебраическоеобозначениеЭлементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение2И2AND3И3AND
- 13. Логическое умножение с отрицаниемГрафическоеобозначениеАлгебраическоеобозначениеЭлементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение2И-НЕ2NAND3И-НЕ3NAND
- 14. Логическое сложение (дизъюнкция)ГрафическоеобозначениеАлгебраическоеобозначениеЭлементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение2ИЛИ2OR3ИЛИ3NOR
- 15. Логическое сложение с отрицаниемГрафическоеобозначениеАлгебраическоеобозначениеЭлементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение2ИЛИ-НЕ2NOR3ИЛИ-НЕ3NOR
- 16. Исключающее ИЛИ (сложение по модулю 2)ГрафическоеобозначениеАлгебраическоеобозначениеЭлементы с
- 17. Свойства логических функций. (Постулаты Булевой алгебры)Джордж Буль1815÷1864Четное количествоЛиния задержки
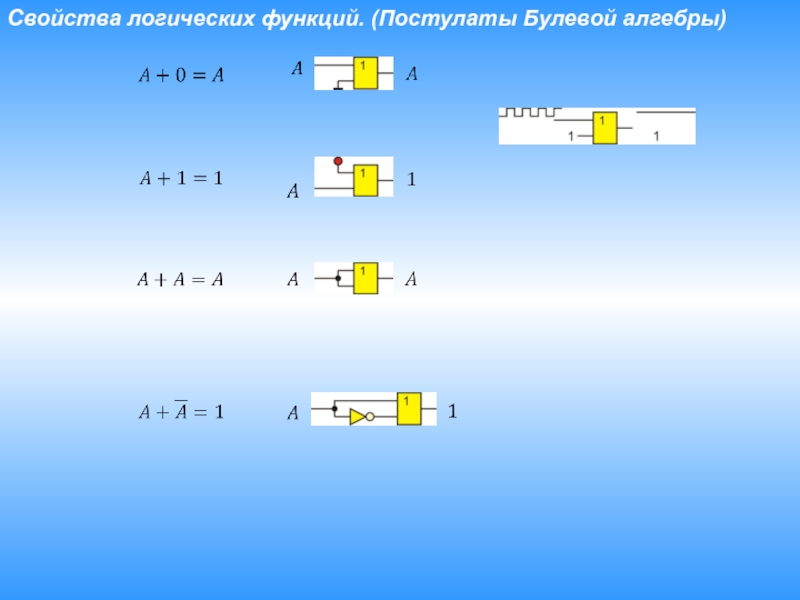
- 18. Свойства логических функций. (Постулаты Булевой алгебры)
- 19. Свойства логических функций. (Постулаты Булевой алгебры)
- 20. Свойства логических функций. (Постулаты Булевой алгебры)
- 21. Законы Булевой алгебрыКоммутативный
- 22. Законы Булевой алгебрыАссоциативный
- 23. Законы Булевой алгебрыДистрибутивный
- 24. Свойства логических функций. (Постулаты Булевой алгебры)Поглощение
- 25. Свойства логических функций. (Постулаты Булевой алгебры)Теорема Де МорганаСледствие теоремы Де Моргана
- 26. Важность учета задержекВ реальных устройствах не совсем так!!
- 27. БазисСколь угодно сложное логическое выражение может быть
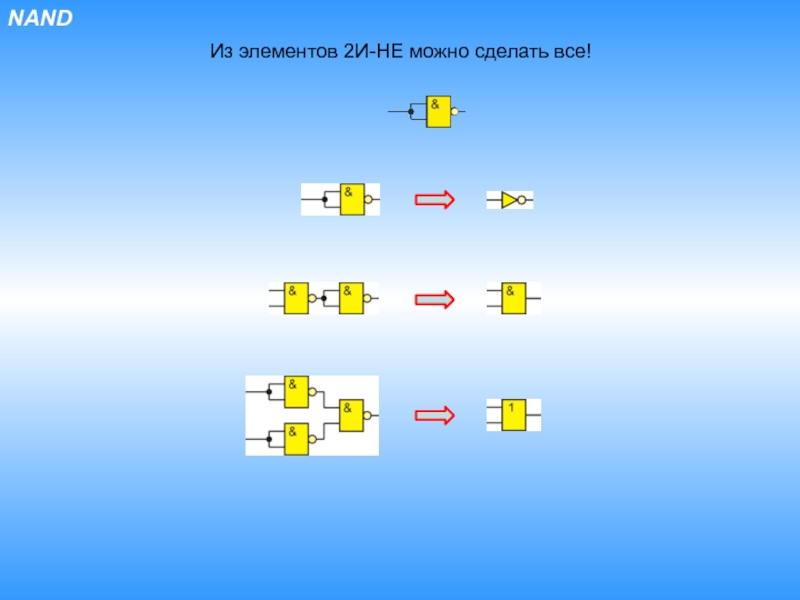
- 28. NANDИз элементов 2И-НЕ можно сделать все!
- 29. Скачать презентанцию
ЛогикаЛОГИКАКомбинаторнаяПоследовательностнаяПреобразование кодовЛогика с памятью
Слайды и текст этой презентации
Слайд 3Преобразование кодов
Таблица истинности
Оригинальная часть.
Выходы
Стандартная часть.
Входы
2n строк
Слайд 5Таблицы истинности
Все комбинации входных сигналов.
Для n входов 2n строк.
Определение функции
Пример:
преобразователь для 3 переменных
Слайд 7Логические функции одной переменной
Буфер
Инвертор
Другое обозначение
Другое обозначение
Другое обозначение
Слайд 8Буферы и преобразователи уровней
Буфер
Buffer
Увеличение нагрузочной способности
Пример: 7407
6 элементов в одном
корпусе
DIP14
SO14
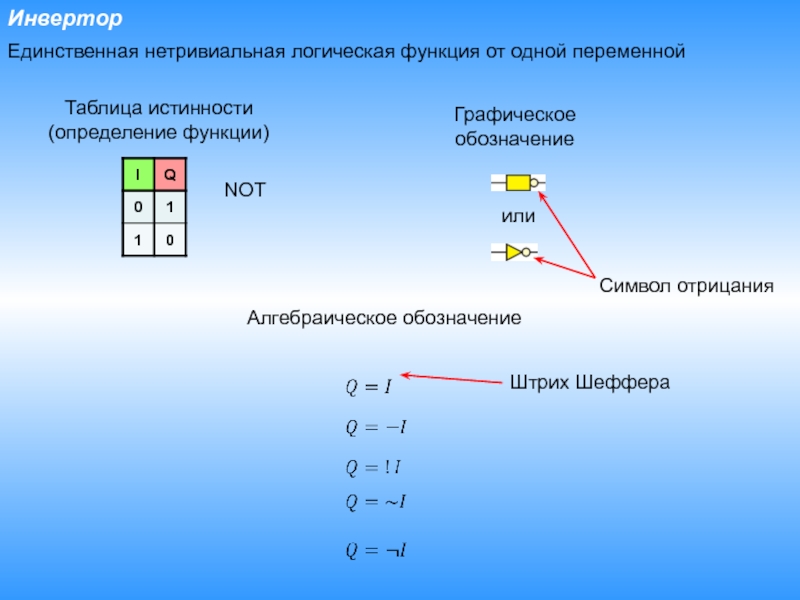
Слайд 10Инвертор
Единственная нетривиальная логическая функция от одной переменной
или
Таблица истинности (определение функции)
Графическое
обозначение
Символ отрицания
Алгебраическое обозначение
Штрих Шеффера
NOT
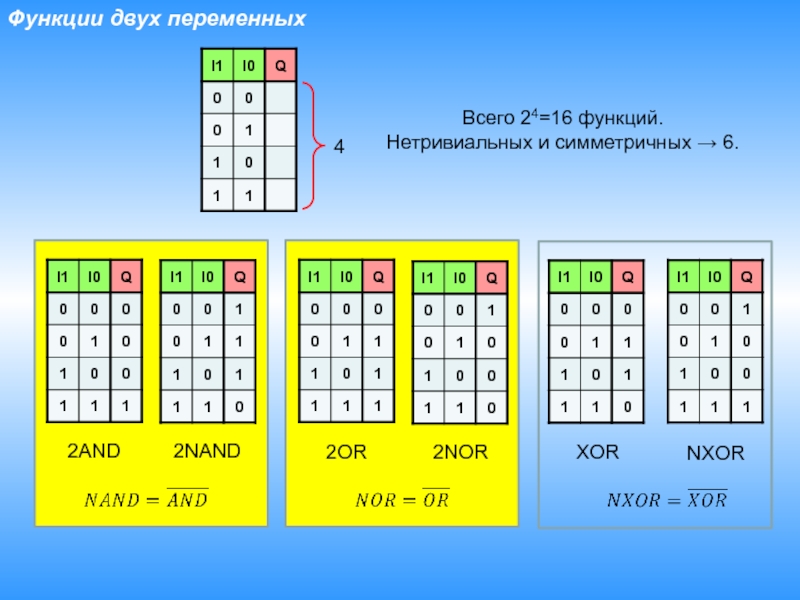
Слайд 11Функции двух переменных
Всего 24=16 функций.
Нетривиальных и симметричных → 6.
2AND
2NAND
2OR
2NOR
XOR
NXOR
4
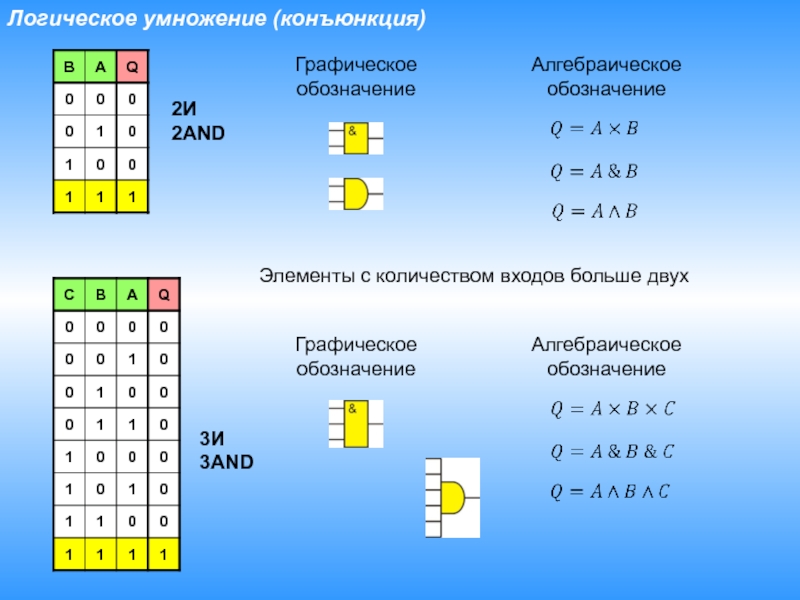
Слайд 12Логическое умножение (конъюнкция)
Графическое
обозначение
Алгебраическое
обозначение
Элементы с количеством входов больше двух
Графическое
обозначение
Алгебраическое
обозначение
2И
2AND
3И
3AND
Слайд 13Логическое умножение с отрицанием
Графическое
обозначение
Алгебраическое
обозначение
Элементы с количеством входов больше двух
Графическое
обозначение
Алгебраическое
обозначение
2И-НЕ
2NAND
3И-НЕ
3NAND
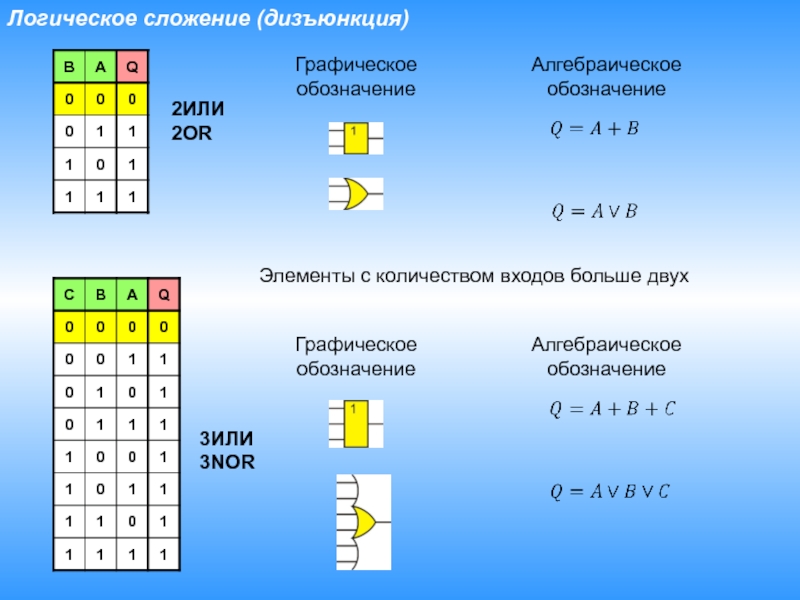
Слайд 14Логическое сложение (дизъюнкция)
Графическое
обозначение
Алгебраическое
обозначение
Элементы с количеством входов больше двух
Графическое
обозначение
Алгебраическое
обозначение
2ИЛИ
2OR
3ИЛИ
3NOR
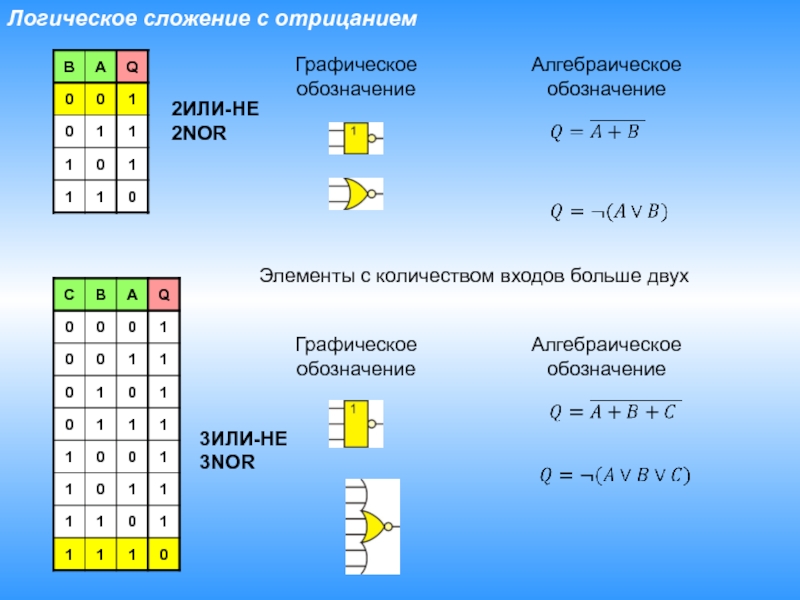
Слайд 15Логическое сложение с отрицанием
Графическое
обозначение
Алгебраическое
обозначение
Элементы с количеством входов больше двух
Графическое
обозначение
Алгебраическое
обозначение
2ИЛИ-НЕ
2NOR
3ИЛИ-НЕ
3NOR
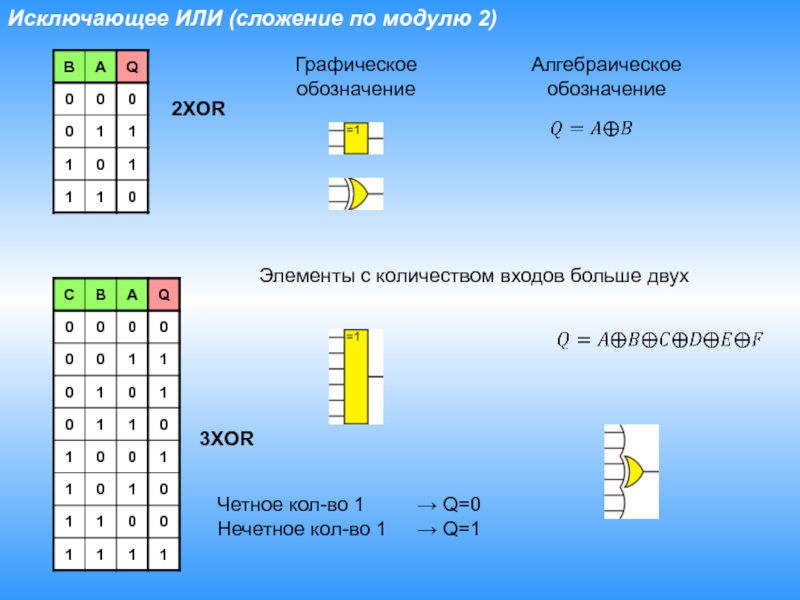
Слайд 16Исключающее ИЛИ (сложение по модулю 2)
Графическое
обозначение
Алгебраическое
обозначение
Элементы с количеством входов больше
двух
2XOR
3XOR
Четное кол-во 1 → Q=0
Нечетное кол-во 1 → Q=1
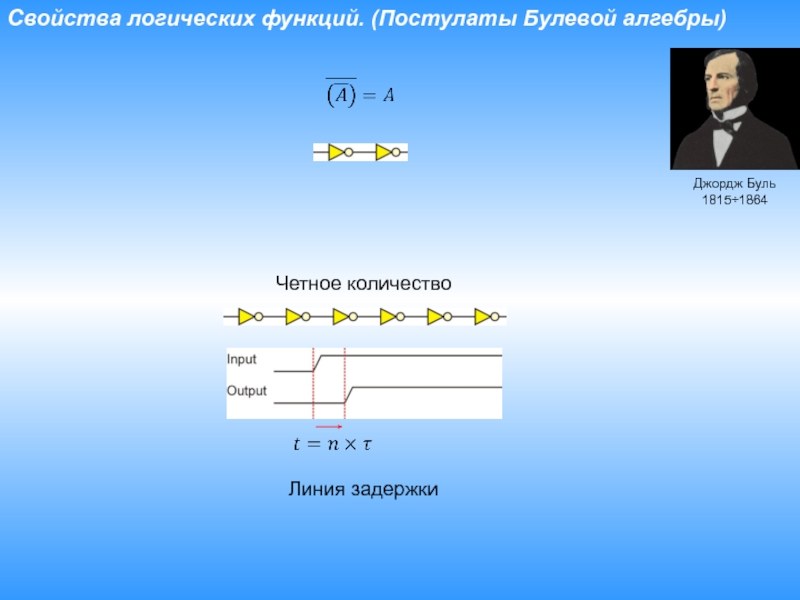
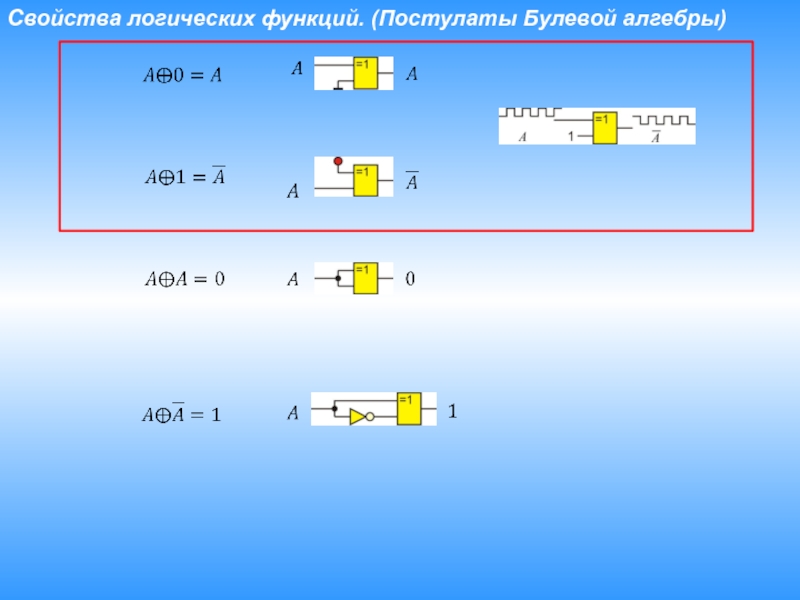
Слайд 17Свойства логических функций. (Постулаты Булевой алгебры)
Джордж Буль
1815÷1864
Четное количество
Линия задержки
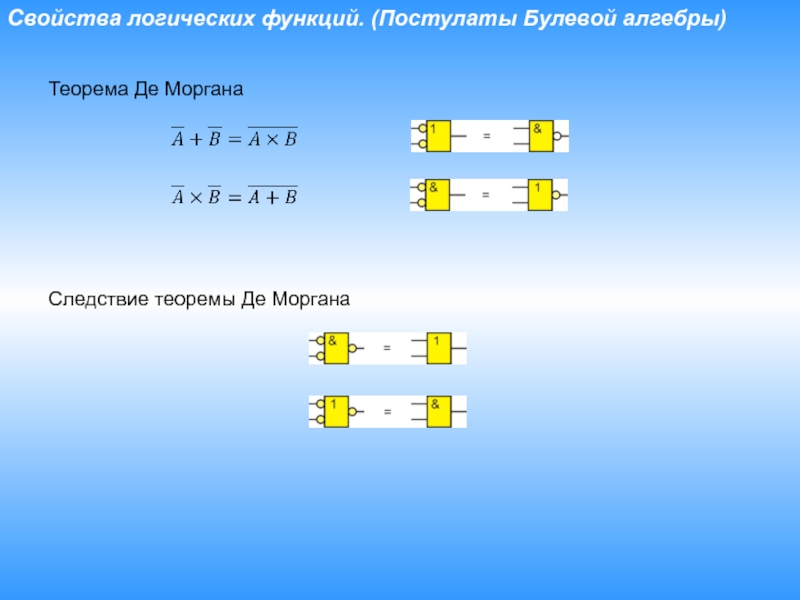
Слайд 25Свойства логических функций. (Постулаты Булевой алгебры)
Теорема Де Моргана
Следствие теоремы Де
Моргана
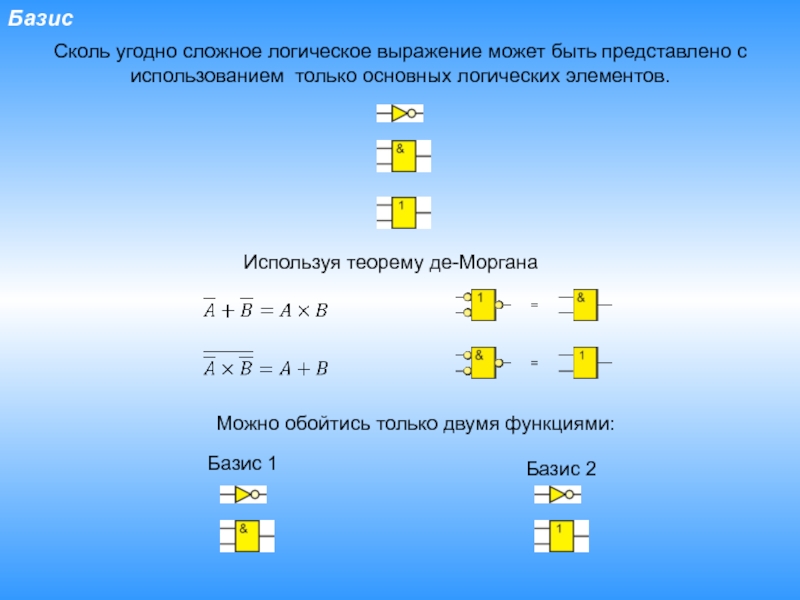
Слайд 27Базис
Сколь угодно сложное логическое выражение может быть представлено с использованием
только основных логических элементов.
Используя теорему де-Моргана
Можно обойтись только двумя функциями:
Базис
1Базис 2