Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
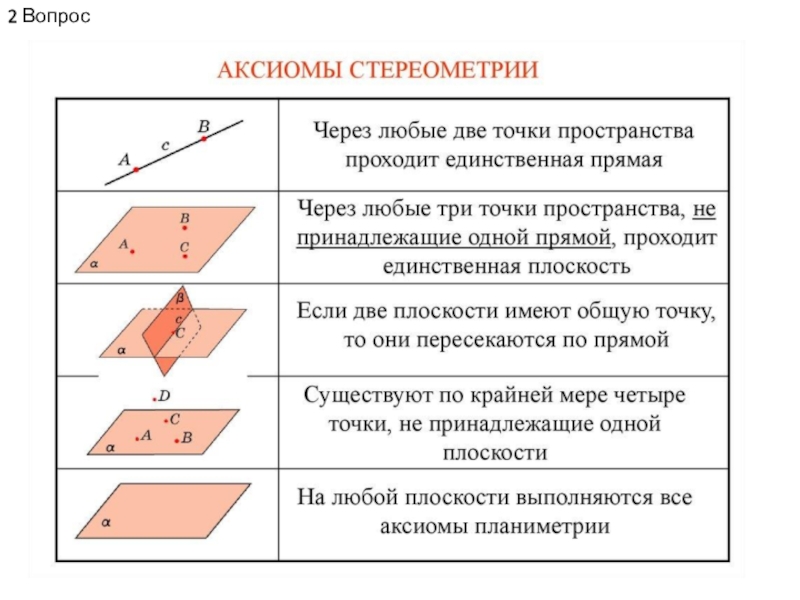
1 Вопрос Стереометрия – раздел в которой изучаются свойства фигур в
Содержание
- 1. 1 Вопрос Стереометрия – раздел в которой изучаются свойства фигур в
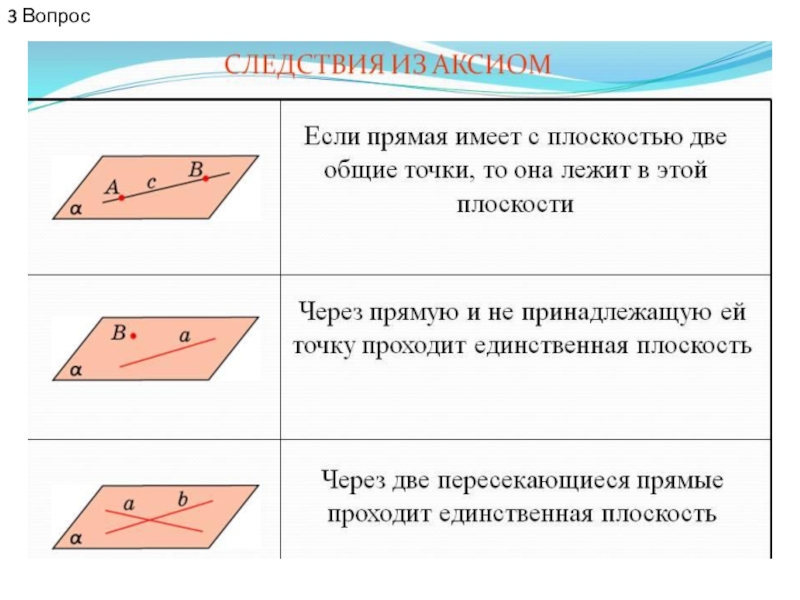
- 2. 2 Вопрос
- 3. 3 Вопрос
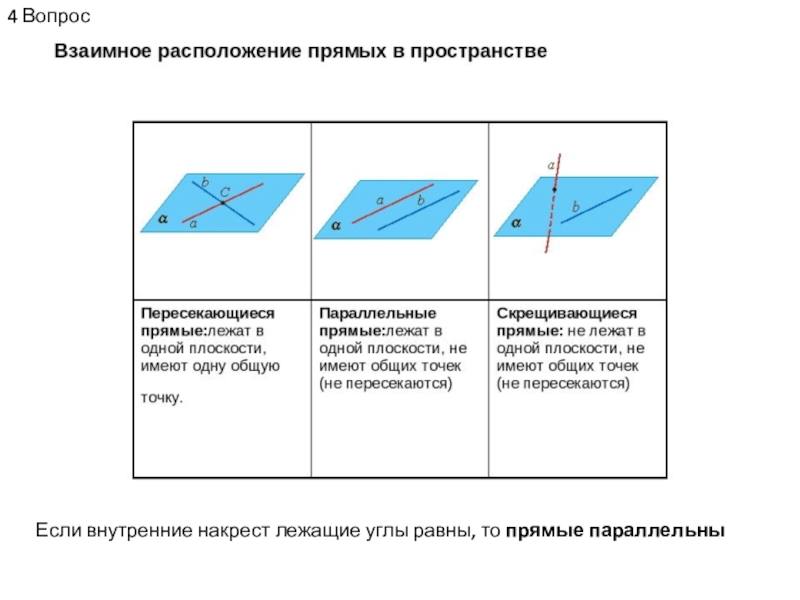
- 4. 4 Вопрос Если внутренние накрест лежащие углы равны, то прямые параллельны
- 5. 5 Вопрос Прямая параллельна плоскости, если она
- 6. 6 Вопрос ТЕОРЕМА (признак параллельности плоскостей). Если
- 7. 7 Вопрос Перпендикулярность плоскостей в четырёхмерном пространстве
- 8. 8 Вопрос Перпендикуляр - Линия, составляющая прямой
- 9. 9 ВопросТеорема о трёх перпендикулярах — фундаментальная
- 10. 10 ВопросДве плоскости называются перпендикулярными (взаимно перпендикулярными),
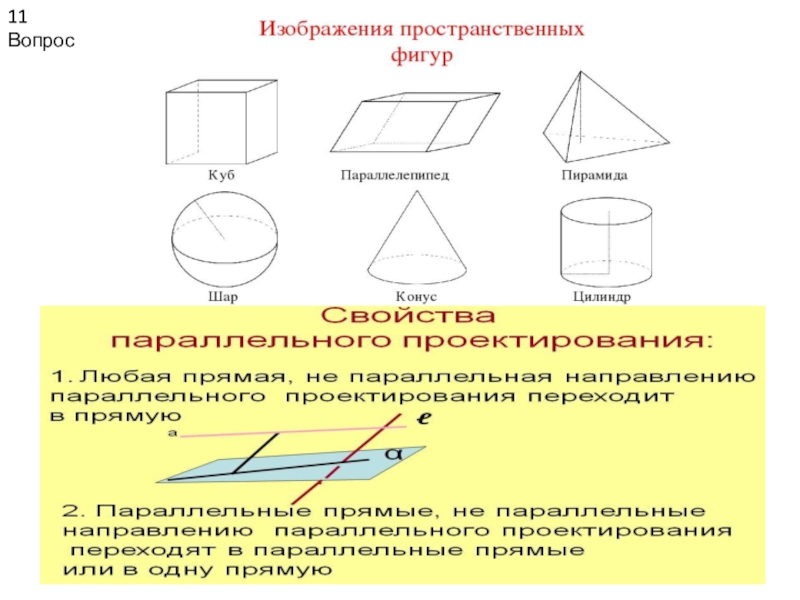
- 11. 11 Вопрос
- 12. 12 Вопросплоскость
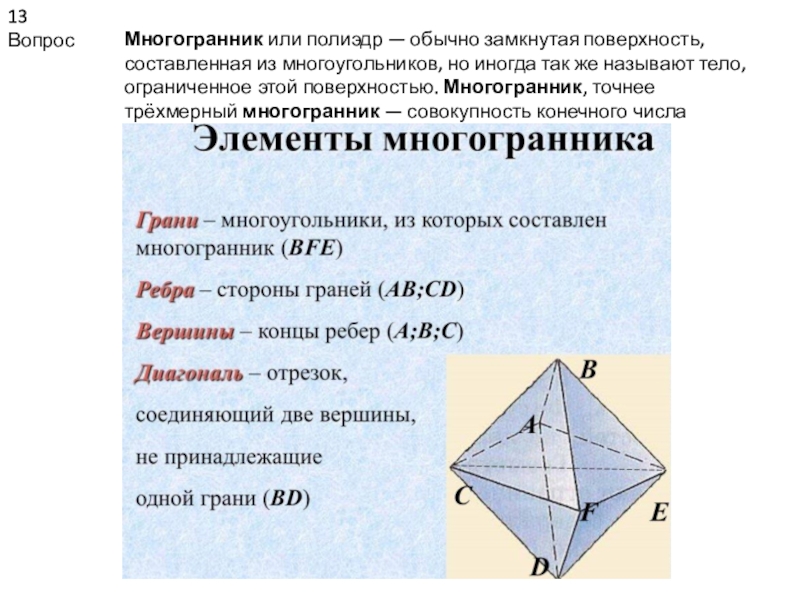
- 13. 13 ВопросМногогранник или полиэдр — обычно замкнутая
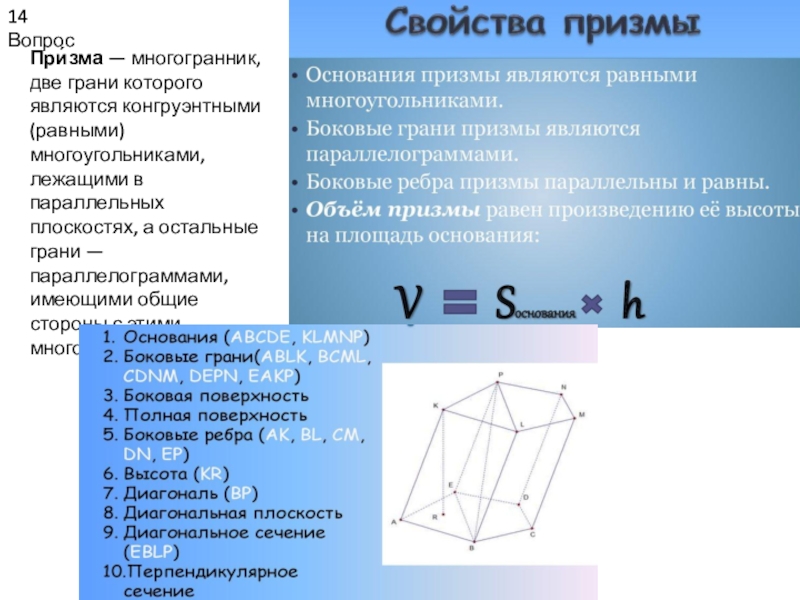
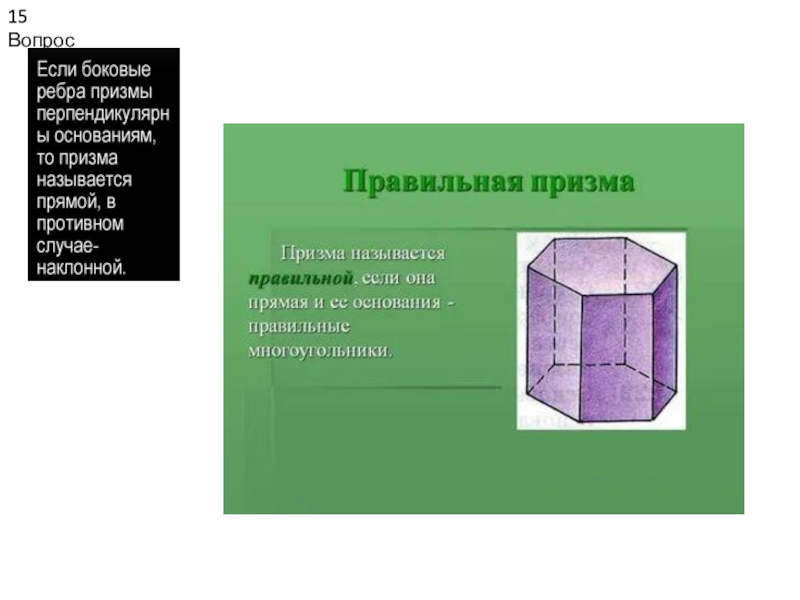
- 14. 14 ВопросПри́зма — многогранник, две грани которого
- 15. 15 Вопрос
- 16. 16 ВопросКвадрат диагонали прямоугольного параллелепипеда равен сумме
- 17. 17 ВопросПрямоугольный параллелепипед — это параллелепипед, у
- 18. 18 ВопросПирамида — многогранник, основание которого — многоугольник, а
- 19. 19 ВопросПирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
- 20. 20 ВопросПлощадью полной поверхности. Sп призмы называется сумма площадей всех ее граней.
- 21. 21 ВопросПравильный многогранник или плато́ново тело —
- 22. 22 Вопрособъем пирамиды равен одной трети, произведения
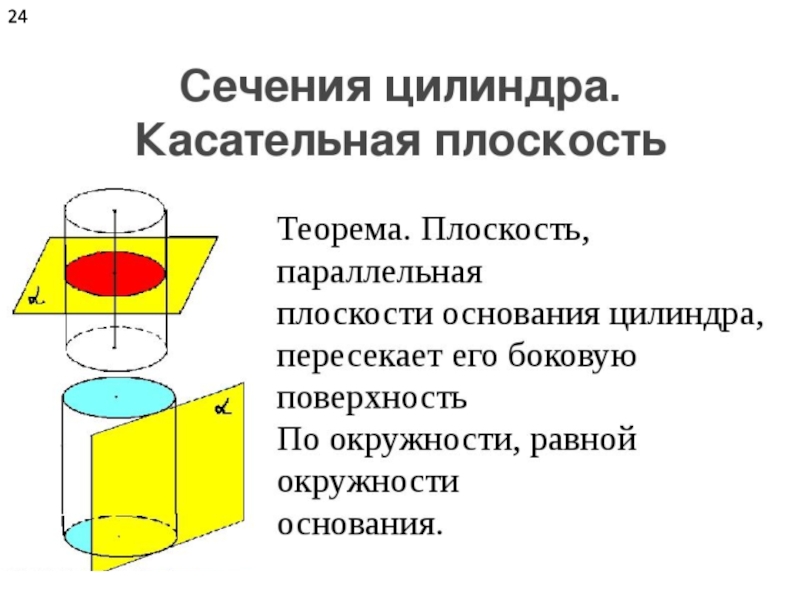
- 23. 23 ВопросЦилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
- 24. 24 Вопрос
- 25. 25 ВопросКонус — тело, полученное объединением всех лучей,
- 26. 26 ВопросУказываем плоскость сечения конуса (зачастую ее
- 27. 27 ВопросСфера— геометрическое место точек в пространстве,
- 28. 28 ВопросА площадь поверхности вращения или поверхности
- 29. 29 ВопросОбъём тела, образуемого при вращении фигуры,
- 30. 30 ВопросУсечённый конус — часть конуса, расположенная между
- 31. 31 Вопрос
- 32. 32 Вопрос
- 33. 33 Вопрос
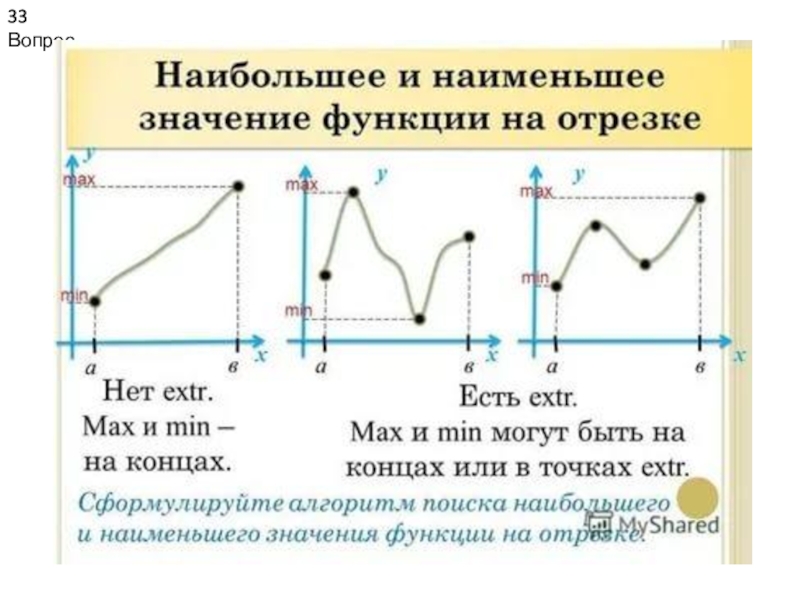
- 34. 34 ВопросКриволине́йная трапе́ция — плоская фигура, ограниченная
- 35. Скачать презентанцию
2 Вопрос
Слайды и текст этой презентации
Слайд 55 Вопрос
Прямая параллельна плоскости, если она параллельна какой-либо прямой,
лежащей в этой плоскости.
Взаимное расположение прямой и плоскости. Прямая (1)
параллельна плоскости (2) тогда и только тогда, когда направляющий вектор этой прямой перпендикулярен нормальному вектору данной плоскости.Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости
Слайд 66 Вопрос
ТЕОРЕМА (признак параллельности плоскостей). Если две пересекающиеся прямые,
лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим
в другой плоскости, то такие плоскости параллельны.Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны
Слайд 77 Вопрос
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла:
плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются
по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости
Слайд 88 Вопрос
Перпендикуляр - Линия, составляющая прямой угол с другой
прямой линией, плоскостью
Наклонная - это линия или плоскость, которая, пересекает
другую линию или плоскость под углом, отличным от угла в 90Проекция (лат. projectio — «выбрасывание вперёд»). изображение трёхмерной фигуры на так называемой картинной (проекционной) плоскости способом, представляющим собой геометрическую идеализацию оптических механизмов.
Слайд 99 Вопрос
Теорема о трёх перпендикулярах — фундаментальная теорема стереометрии. Прямая,
проведённая в плоскости через основание наклонной перпендикулярно к её проекции
на эту плоскость, перпендикулярна и самой наклонной.Аналогично теореме о трех перпендикулярах если прямая с перпендикулярна наклонной CA, то она, будучи перпендикулярна и прямой CA`, перпендикулярна плоскости β, а значит, и проекции наклонной BC.
Слайд 1010 Вопрос
Две плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между
ними равен 90° Теорема. (признак перпендикулярности двух плоскостей). Если одна
из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Слайд 1313 Вопрос
Многогранник или полиэдр — обычно замкнутая поверхность, составленная из
многоугольников, но иногда так же называют тело, ограниченное этой поверхностью.
Многогранник, точнее трёхмерный многогранник — совокупность конечного числа
Слайд 1414 Вопрос
При́зма — многогранник, две грани которого являются конгруэнтными (равными)
многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами,
имеющими общие стороны с этими многоугольниками.
Слайд 1616 Вопрос
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его
измерений: d² = a² + b² + c². Доказательство: Все
грани прямоугольного параллелепипеда - прямоугольники.Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм.
Слайд 1717 Вопрос
Прямоугольный параллелепипед — это параллелепипед, у которого все грани
прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:
d² = a² + b² + c². Доказательство: Все грани прямоугольного параллелепипеда - прямоугольники. ΔABD: ∠BAD = 90°, по теореме Пифагора d₁² = a² + b² ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора d² = d₁² + c² = a² + b² + c² d² = a² + b² + c² Доказанная теорема - пространственная теорема Пифагора.
Слайд 1818 Вопрос
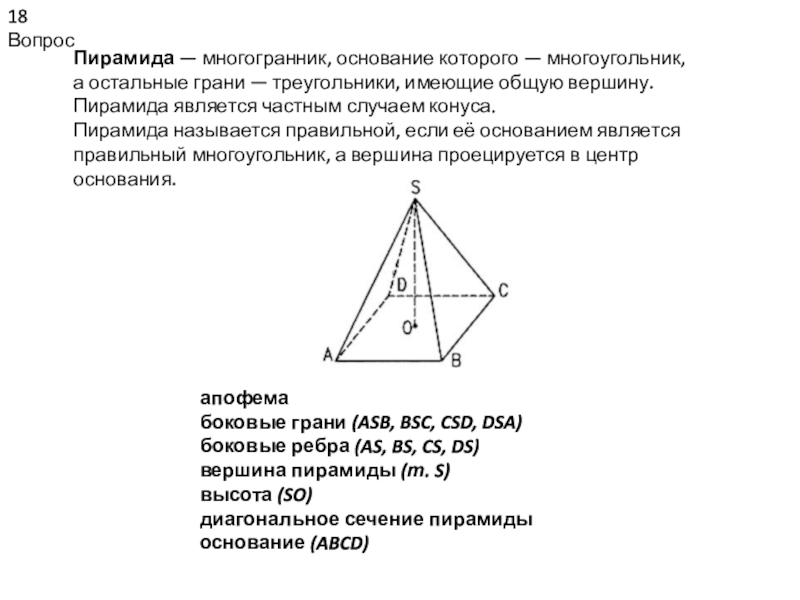
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники,
имеющие общую вершину.
Пирамида является частным случаем конуса.
Пирамида называется правильной, если
её основанием является правильный многоугольник, а вершина проецируется в центр основания.апофема
боковые грани (ASB, BSC, CSD, DSA)
боковые ребра (AS, BS, CS, DS)
вершина пирамиды (т. S)
высота (SO)
диагональное сечение пирамиды
основание (ABCD)
Слайд 1919 Вопрос
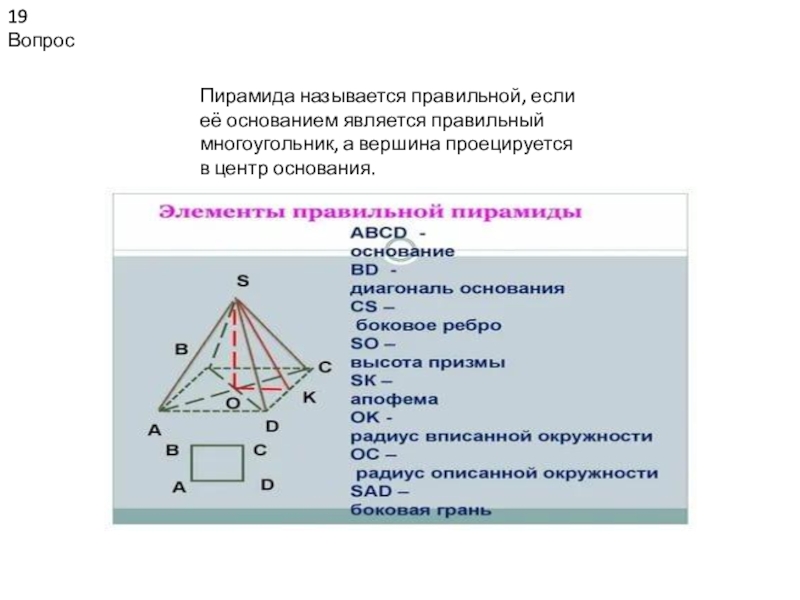
Пирамида называется правильной, если её основанием является правильный многоугольник,
а вершина проецируется в центр основания.
Слайд 2121 Вопрос
Правильный многогранник или плато́ново тело — это выпуклый многогранник,
состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
Слайд 2222 Вопрос
объем пирамиды равен одной трети, произведения площади основания на
высоту. Объём призмы равен произведению её высоты на площадь основания
Слайд 2323 Вопрос
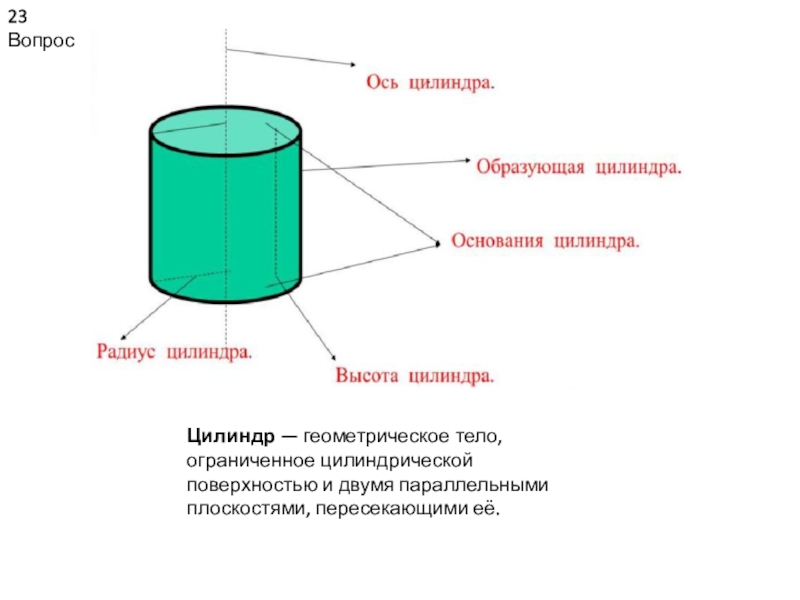
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными
плоскостями, пересекающими её.
Слайд 2525 Вопрос
Конус — тело, полученное объединением всех лучей, исходящих из одной
точки (вершины конуса) и проходящих через плоскую поверхность.
Круглый конус может
быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
Слайд 2626 Вопрос
Указываем плоскость сечения конуса (зачастую ее располагают под произвольным
углом) 3. Воспользуемся методом вспомогательных секущих плоскостей (они необходимы для
детального построения сечения конуса). Расстояние между секущими плоскостями берем произвольно. 4. Находим вид сечения на нижнем рисунке (виде сверху) 5. Затем определим точки на виде слева.
Слайд 2727 Вопрос
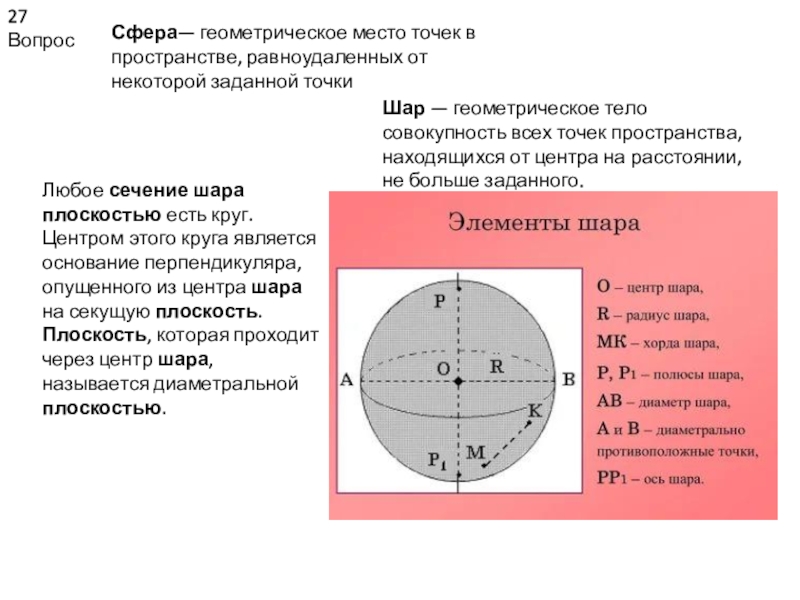
Сфера— геометрическое место точек в пространстве, равноудаленных от некоторой
заданной точки
Шар — геометрическое тело совокупность всех точек пространства, находящихся от
центра на расстоянии, не больше заданного.Любое сечение шара плоскостью есть круг. Центром этого круга является основание перпендикуляра, опущенного из центра шара на секущую плоскость. Плоскость, которая проходит через центр шара, называется диаметральной плоскостью.
Слайд 2828 Вопрос
А площадь поверхности вращения или поверхности тела вращения -
это его внешняя оболочка, не считая кругов, образованных вращением вокруг
оси прямых x = a и x = b.
Слайд 2929 Вопрос
Объём тела, образуемого при вращении фигуры, лежащей в плоскости
целиком по одну сторону от оси вращения, равен произведению площади
фигуры на длину окружности, пробегаемой центром масс этой фигуры.
Слайд 3030 Вопрос
Усечённый конус — часть конуса, расположенная между его основанием и
секущей плоскостью, параллельной основанию.
Усечённая пирамида — часть пирамиды, заключенная между её
основанием, боковыми гранями и сечением этой пирамиды плоскостью, параллельной основанию.
Слайд 3434 Вопрос
Криволине́йная трапе́ция — плоская фигура, ограниченная графиком неотрицательной непрерывной
функции. , определенной на отрезке [a; b], осью абсцисс и
прямыми. и. . Для нахождения площади криволинейной трапеции.![34 ВопросКриволине́йная трапе́ция — плоская фигура, ограниченная графиком неотрицательной непрерывной функции. , определенной на отрезке [a; b],](/img/tmb/6/580376/afc2e3fd24a2c3ae450d3f8a12a8c994-800x.jpg "1 Вопрос
Стереометрия – раздел в которой изучаются свойства фигур в 34 ВопросКриволине́йная трапе́ция — плоская фигура, ограниченная графиком неотрицательной непрерывной функции.")
