Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция_2.ppt
Содержание
- 1. Лекция_2.ppt
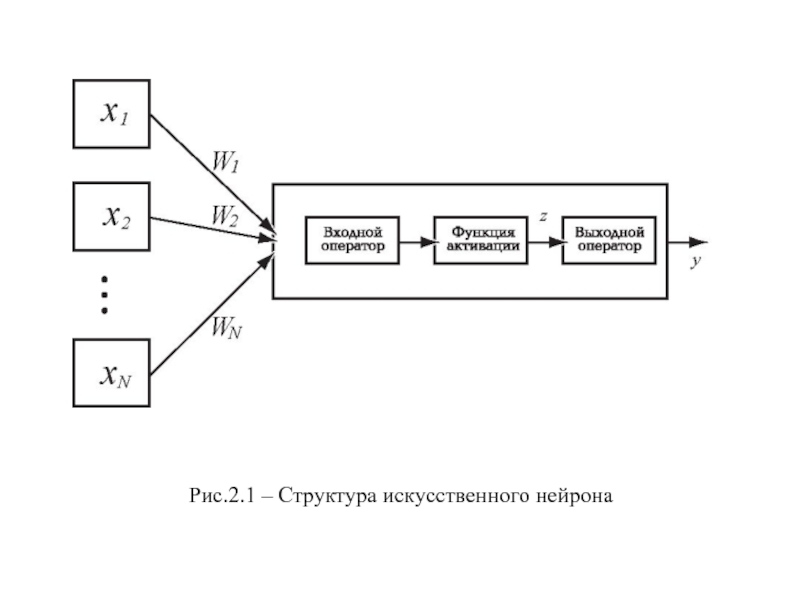
- 2. Рис.2.1 – Структура искусственного нейрона
- 3. Входной оператор- сумма взвешенных входов; - максимальное
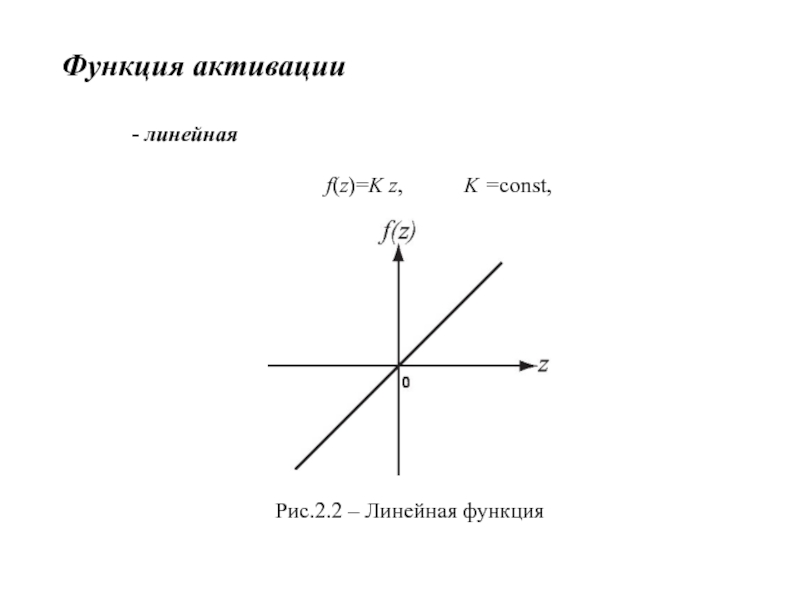
- 4. Функция активации- линейная
- 5. - линейная биполярная с насыщением Рис.2.3 – Линейная с насыщением
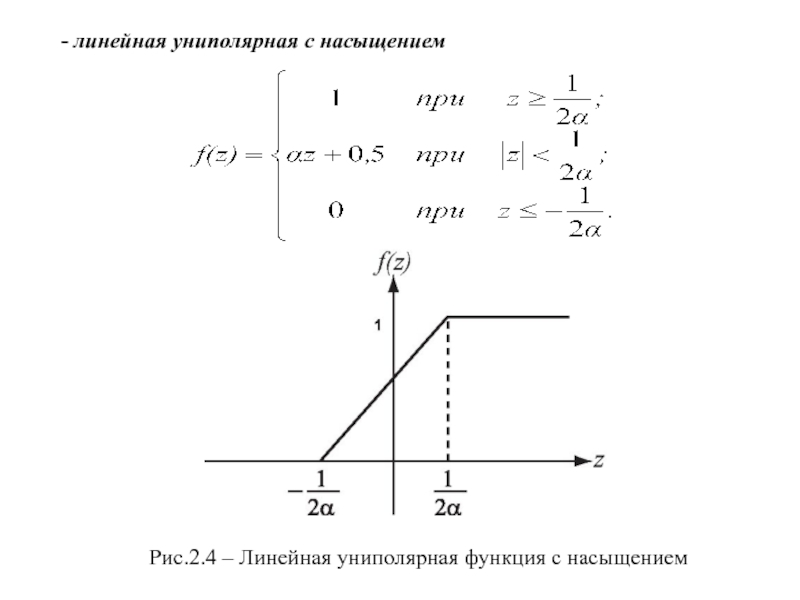
- 6. - линейная униполярная с насыщением
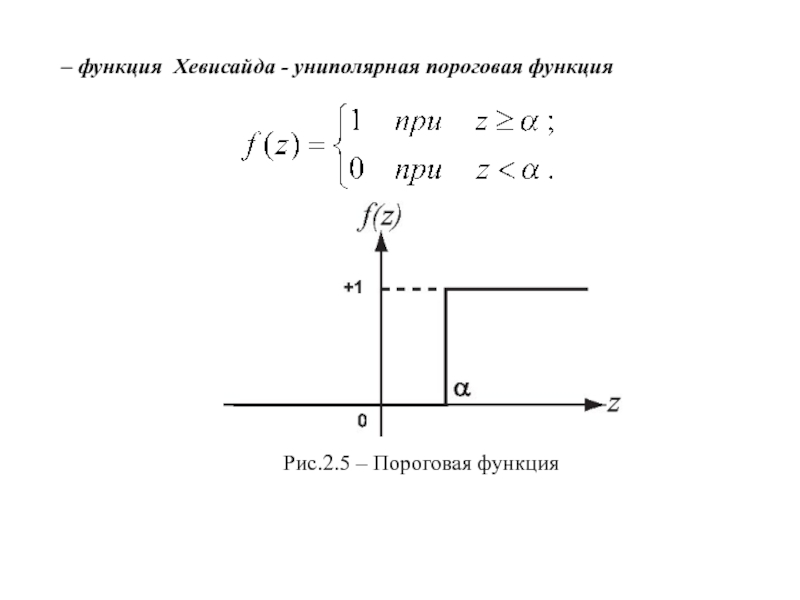
- 7. – функция Хевисайда - униполярная пороговая функцияРис.2.5 – Пороговая функция
- 8. – биполярная пороговая функцияРис.2.6 – Биполярная пороговая функция
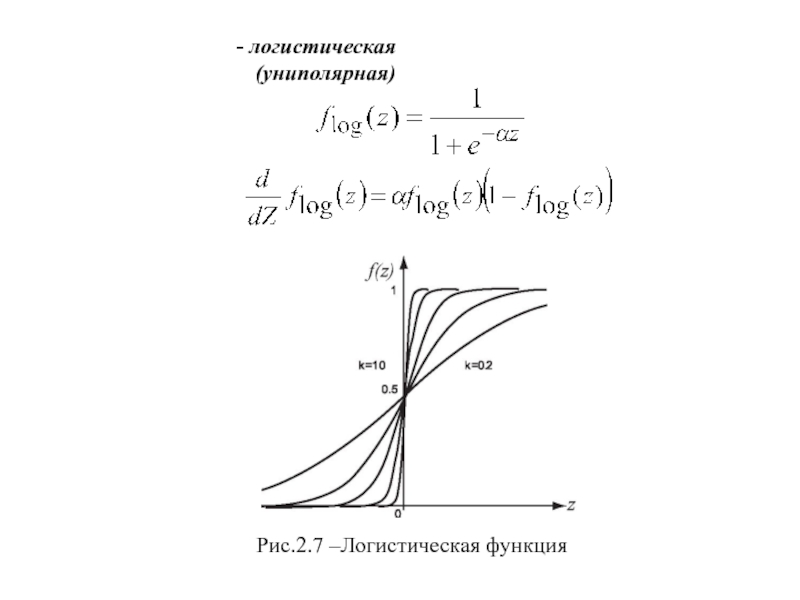
- 9. - логистическая (униполярная) Рис.2.7 –Логистическая функция
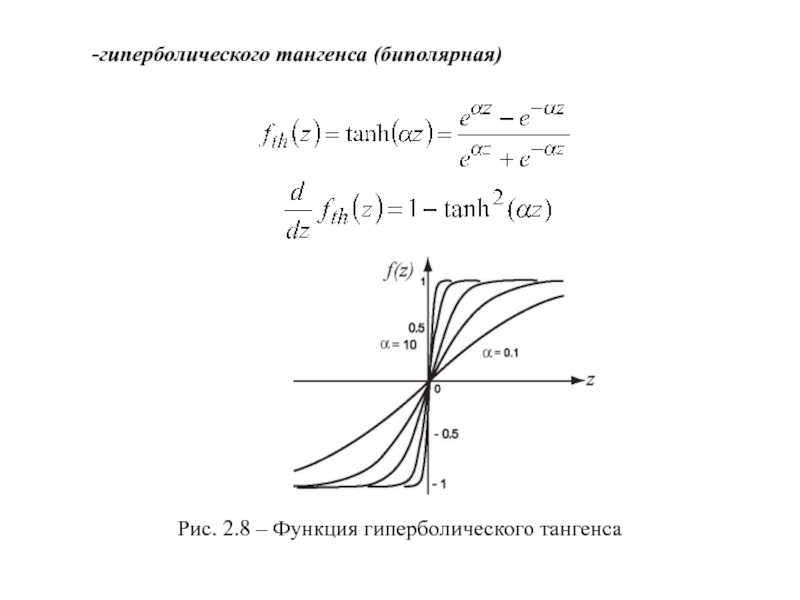
- 10. -гиперболического тангенса (биполярная)
- 11. Выражение логистической функции и функции гиперболического тангенса друг через друга:
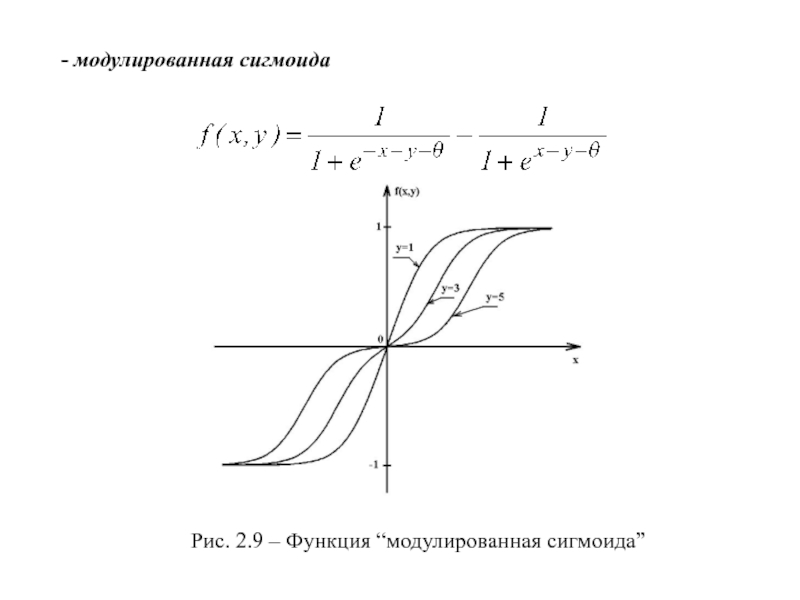
- 12. - модулированная сигмоидаРис. 2.9 – Функция “модулированная сигмоида”
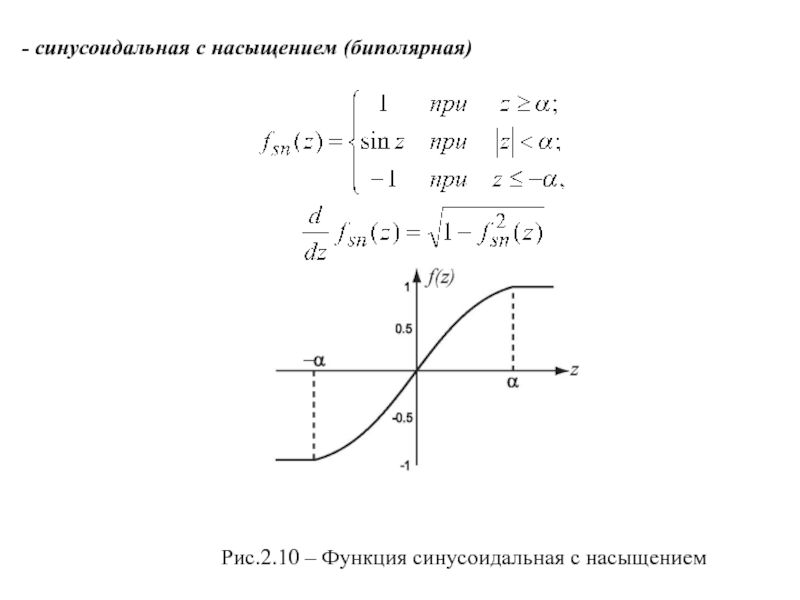
- 13. - синусоидальная с насыщением (биполярная)Рис.2.10 – Функция синусоидальная с насыщением
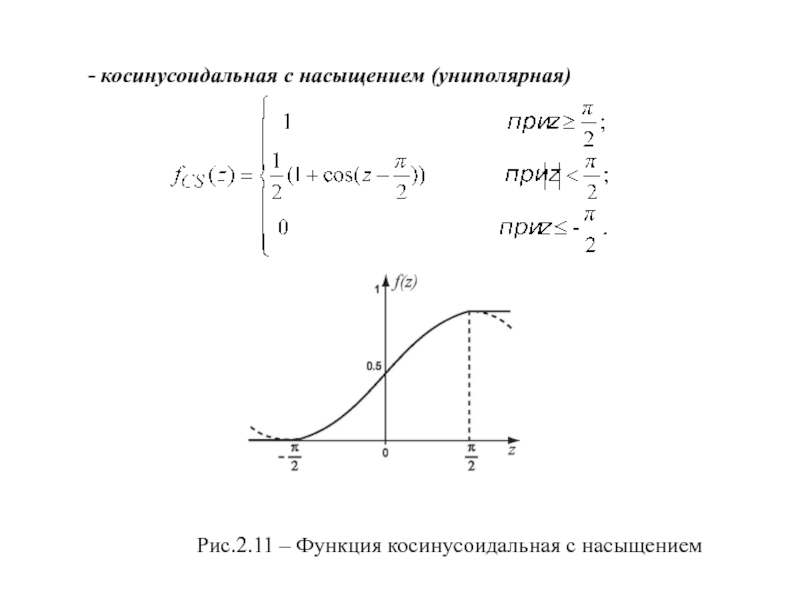
- 14. - косинусоидальная с насыщением (униполярная) Рис.2.11 – Функция косинусоидальная с насыщением
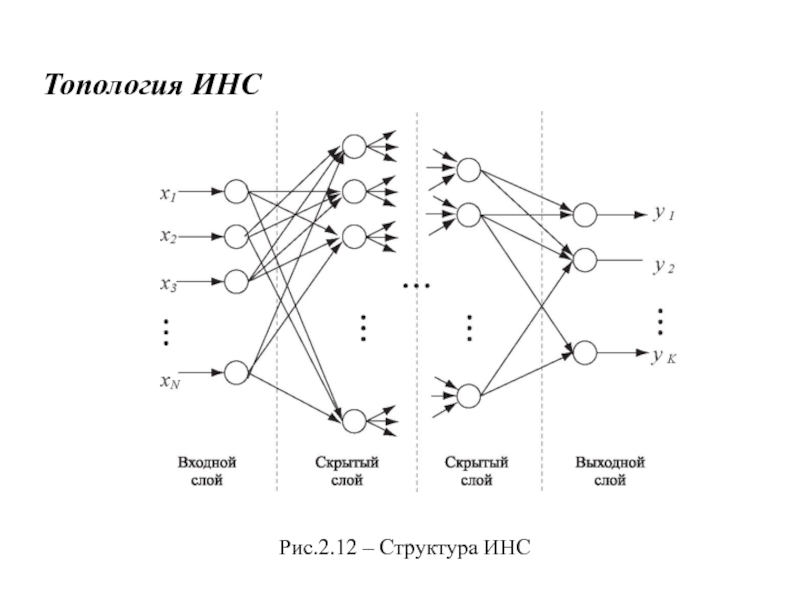
- 15. Топология ИНСРис.2.12 – Структура ИНС
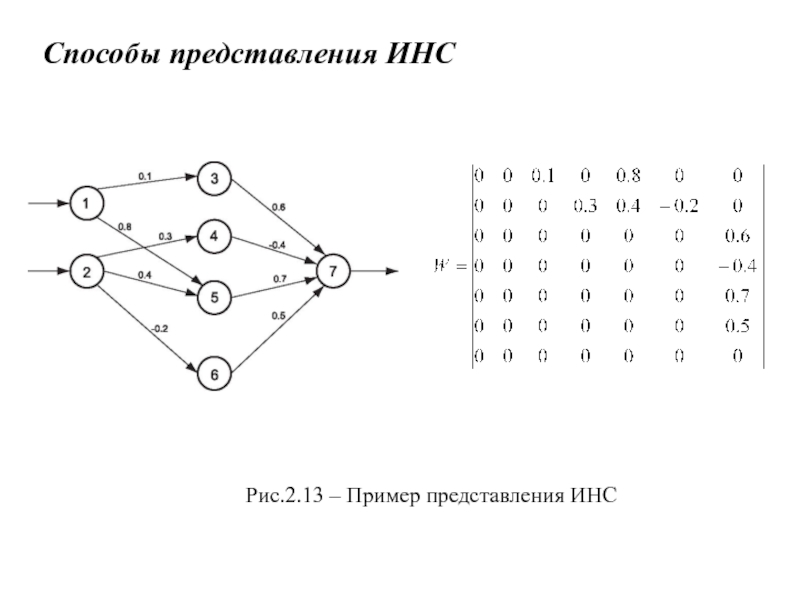
- 16. Способы представления ИНСРис.2.13 – Пример представления ИНС
- 17. Топологии ИНС:1. ИНС без обратных связей (прямого
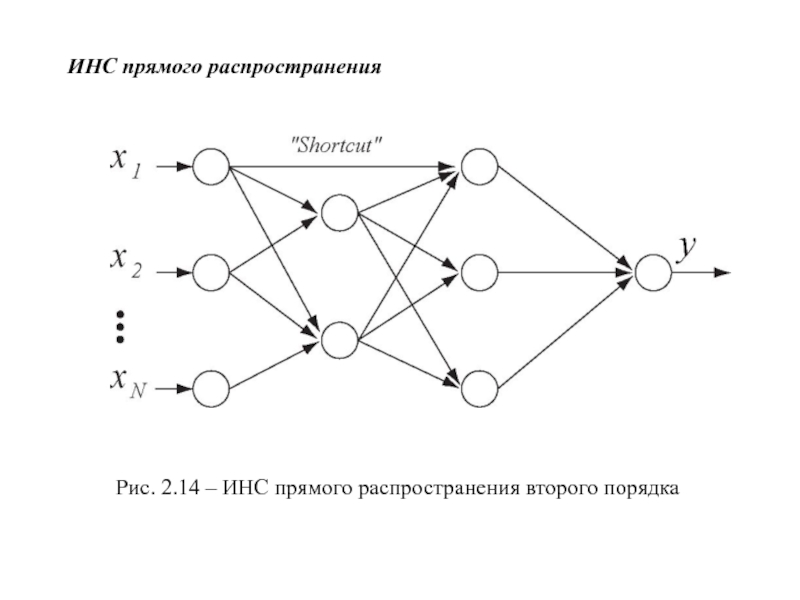
- 18. ИНС прямого распространения Рис. 2.14 – ИНС прямого распространения второго порядка
- 19. ИНС обратного распространения Рис.2.15 – ИНС с прямыми обратными связями
- 20. Рис.2.16 – ИНС с непрямыми обратными связями
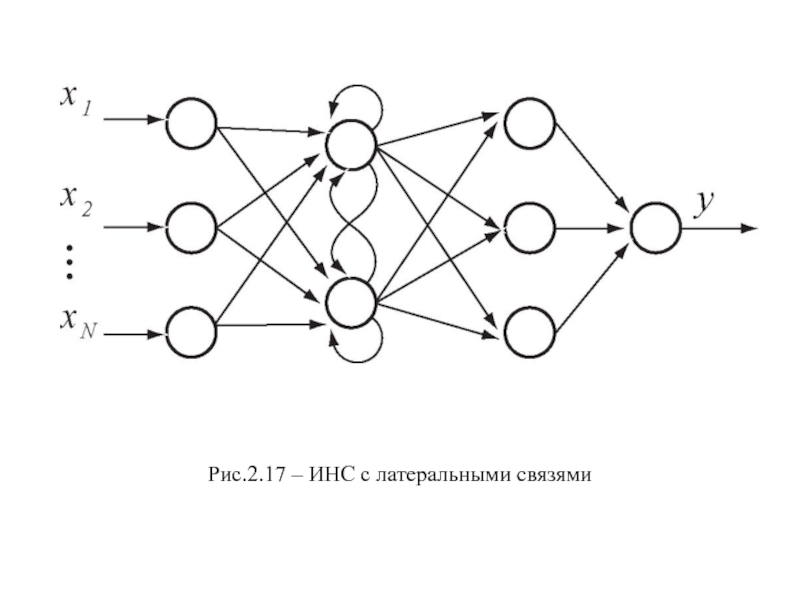
- 21. Рис.2.17 – ИНС с латеральными связями
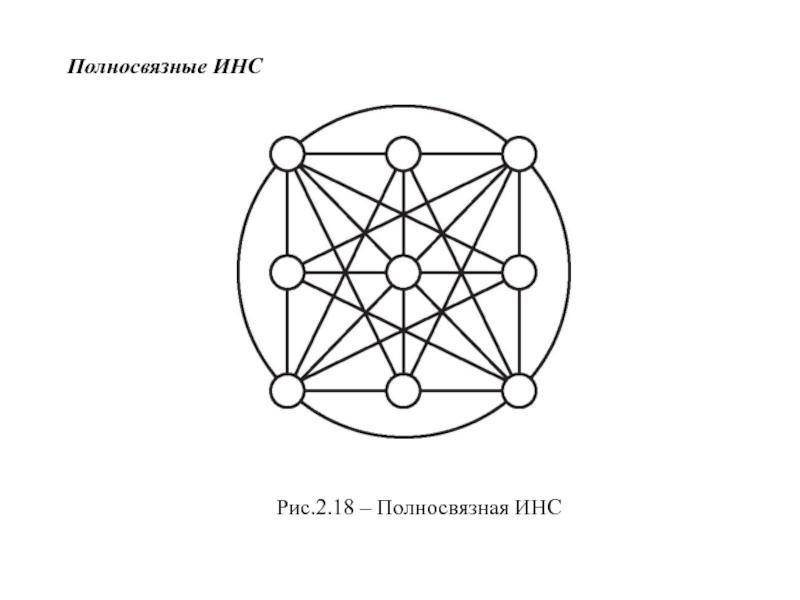
- 22. Полносвязные ИНСРис.2.18 – Полносвязная ИНС
- 23. Подходы к обучению ИНС:- изменение конфигурации сети
- 24. Рис.2.19 – Модель искусственного нейрона
- 25. Типы обучения ИНС:- Обучение с учителем;- Обучение без учителя;- Подкрепляемое обучение.
- 26. Правило обучения Хэбба (коррелятивное,соотносительное обучение), В векторном
- 27. Дельта-правилоРасширенное дельта-правило
- 28. Конкурентное обучение;Стохастическое обучение;Градиентные методы обучения где γ - коэффициент, влияющий на скорость обучения;
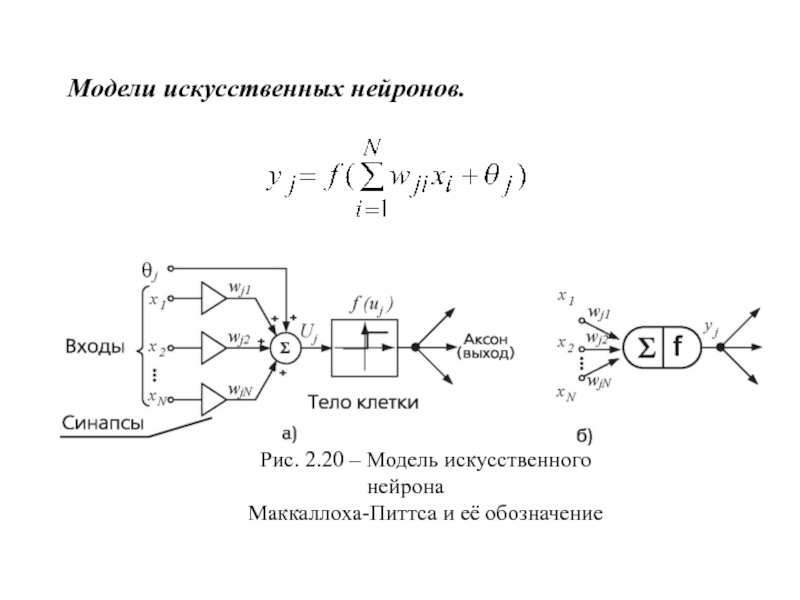
- 29. Модели искусственных нейронов.Рис. 2.20 – Модель искусственного нейронаМаккаллоха-Питтса и её обозначение
- 30. Рис. 2.21 – Электронная аналоговая модель нейронной клетки
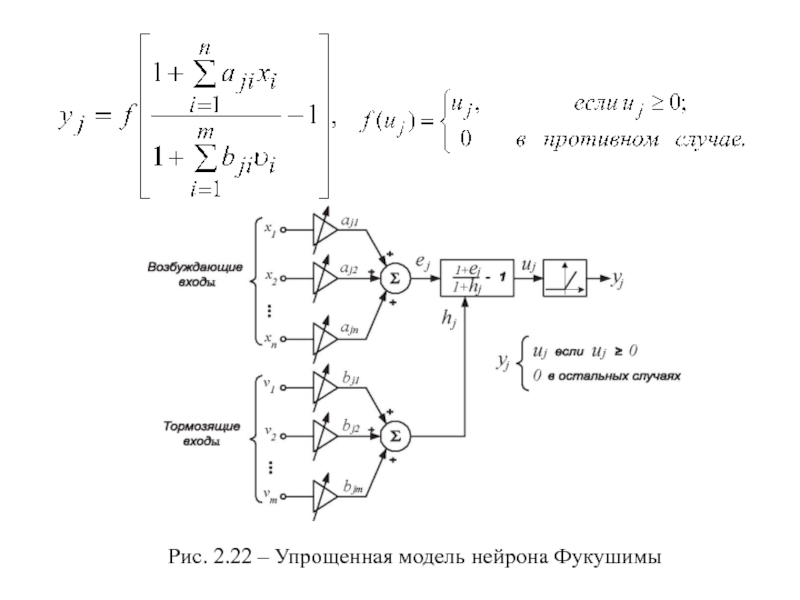
- 31. Рис. 2.22 – Упрощенная модель нейрона Фукушимы
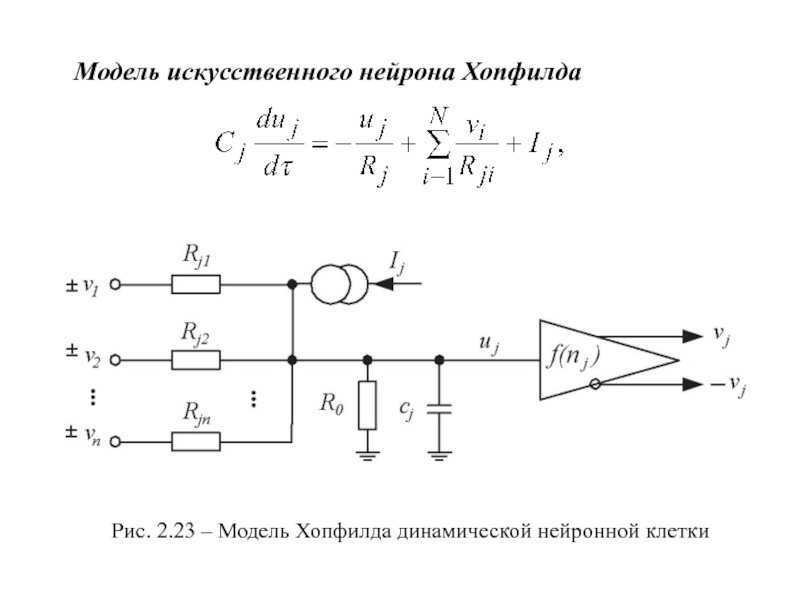
- 32. Модель искусственного нейрона Хопфилда Рис. 2.23 – Модель Хопфилда динамической нейронной клетки
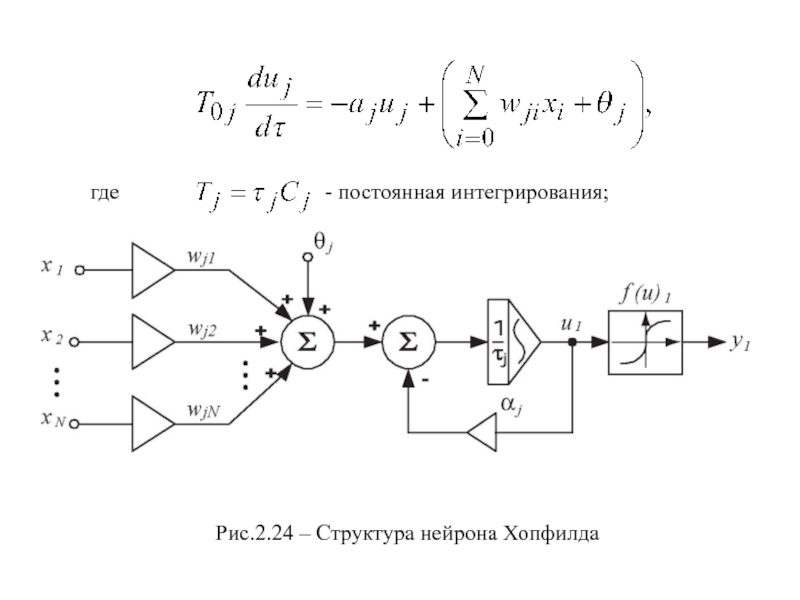
- 33. Рис.2.24 – Структура нейрона Хопфилда -
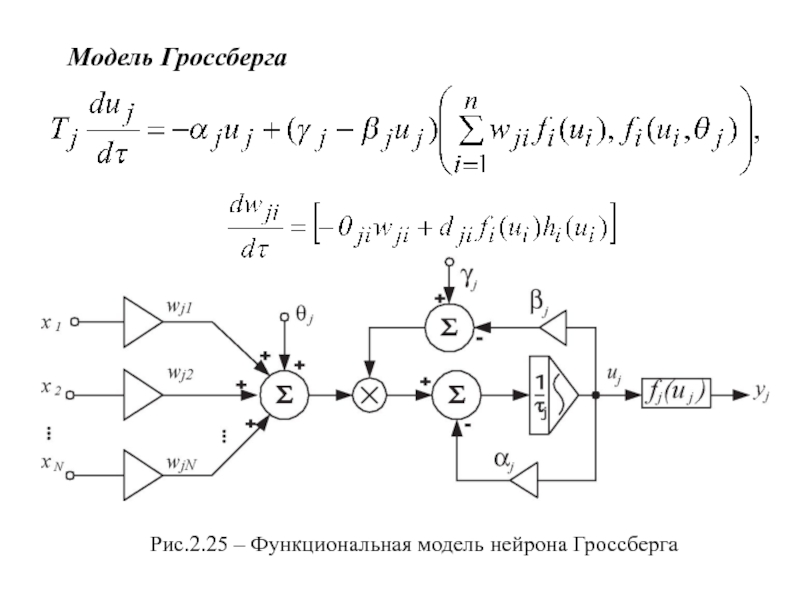
- 34. Модель ГроссбергаРис.2.25 – Функциональная модель нейрона Гроссберга
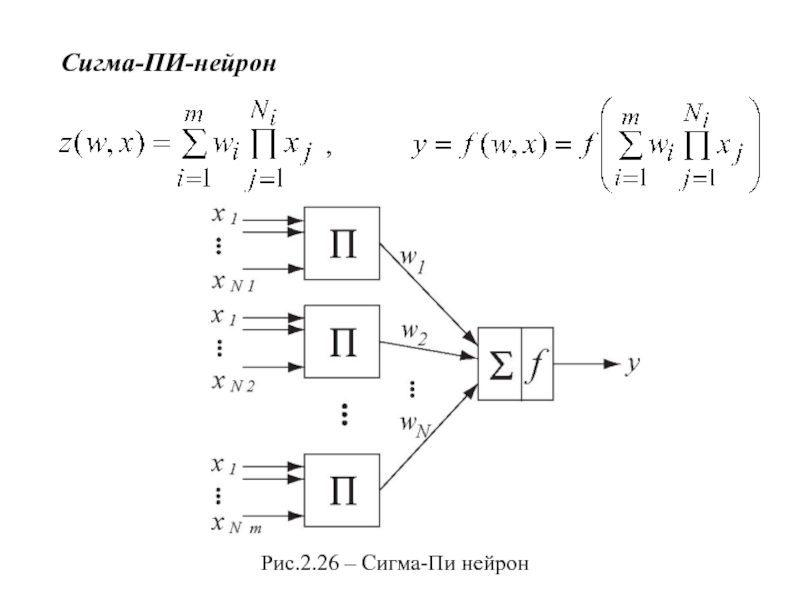
- 35. Сигма-ПИ-нейрон , Рис.2.26 – Сигма-Пи нейрон
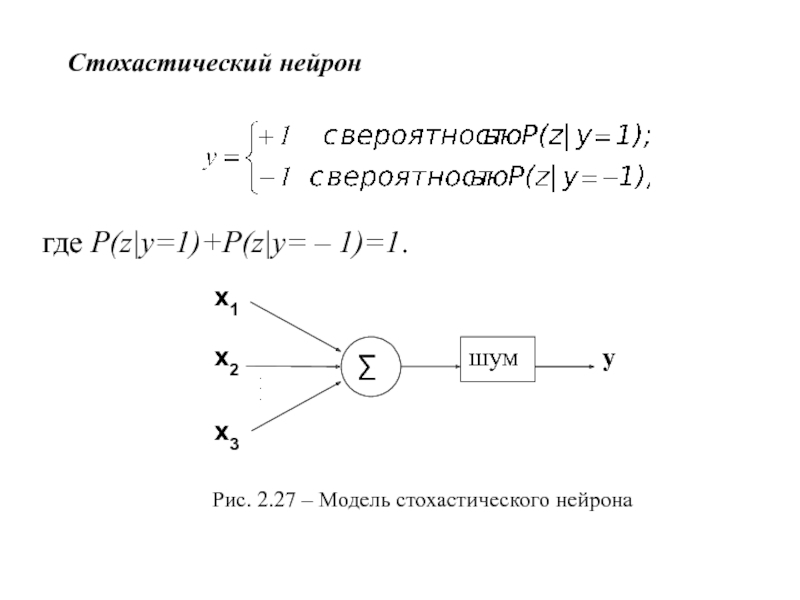
- 36. Стохастический нейрон где P(z|y=1)+P(z|y= – 1)=1.Рис. 2.27 – Модель стохастического нейрона
- 37. Скачать презентанцию
Рис.2.1 – Структура искусственного нейрона
Слайды и текст этой презентации
Слайд 14- косинусоидальная с насыщением (униполярная)
Рис.2.11 – Функция косинусоидальная с
насыщением
Слайд 17Топологии ИНС:
1. ИНС без обратных связей (прямого распространения, feed-forvard)
- первого
порядка;
- второго порядка (c “shortcut connections”).
2. ИНС с обратными связями
(обратного распространения, рекуррентные, Feedback)
- с прямыми обратными связями (direct feedback);
- с непрямыми обратными связями (indirect feedback);
- с латеральными связями (lateral feedback);
- полносвязные.
Слайд 23Подходы к обучению ИНС:
- изменение конфигурации сети путем образования новых
или исключения некоторых существующих связей между
нейронами;
- изменение элементов матрицы
связи (весов);- изменение характеристик нейронов (вида и параметров
активационной функции и т.д.).
Слайд 26Правило обучения Хэбба (коррелятивное,
соотносительное обучение)
,
В векторном виде данное правило
может быть записано
следующим образом:
для непрерывного времени
для дискретного времени
.