Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
correl2.ppt
Содержание
- 1. correl2.ppt
- 2. Виды и формы связи между явлениями
- 3. Функциональная связьПри функциональной связи каждому значению факторного
- 4. Стохастическая связьСвязь между случайными величинами называется стохастической.
- 5. При статистической связи одному и тому же
- 6. Основные приемы изучения взаимосвязей Для изучения, измерения
- 7. Метод сравнения параллельных рядовПриводится ряд данных по
- 8. Пример: Предположим, нужно выяснить, есть ли зависимость
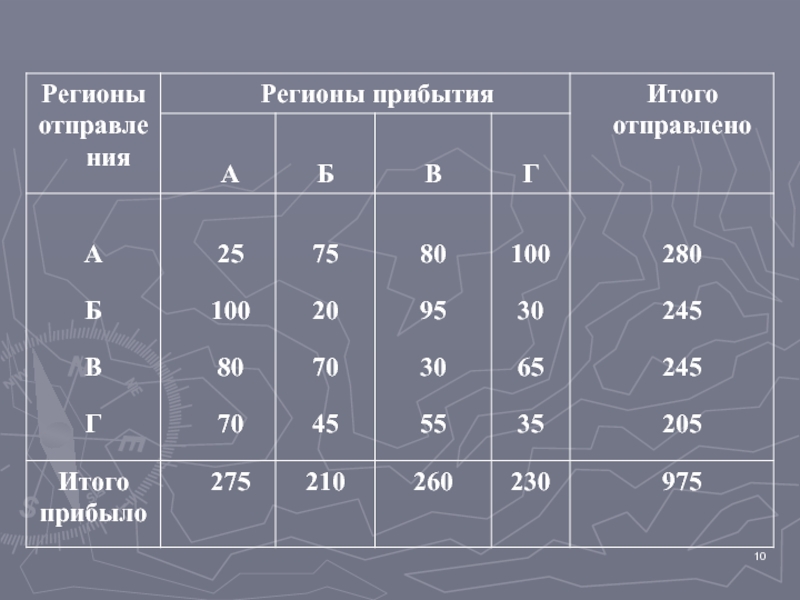
- 9. Балансовый метод состоит в том, что данные
- 10. Слайд 10
- 11. Графический метод может использоваться как самостоятельно, так
- 12. Беспорядочное расположение говорит об отсутствии связи. Напротив,
- 13. Метод аналитической группировкиЕдиницы статистической совокупности группируются, как
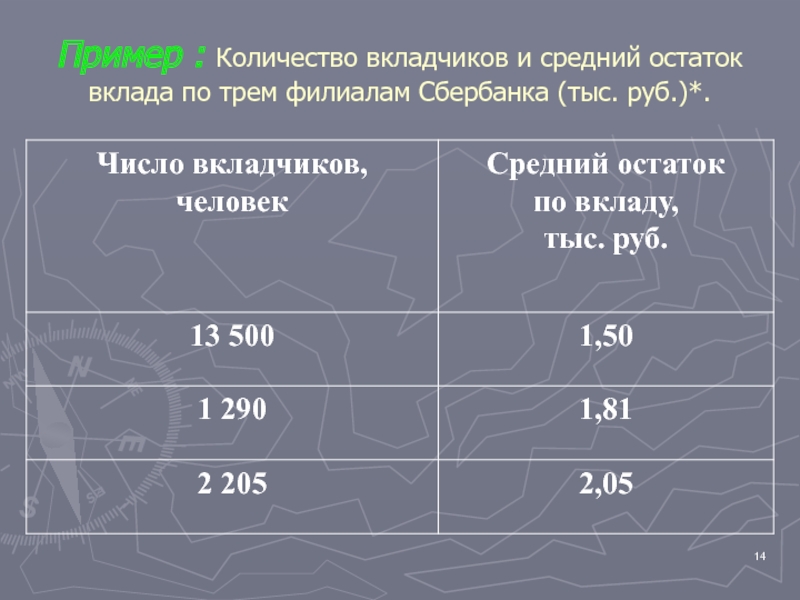
- 14. Пример : Количество вкладчиков и средний остаток вклада по трем филиалам Сбербанка (тыс. руб.)*.
- 15. Дисперсионный анализ дает прежде всего возможность определить
- 16. Анализ проходит четыре итерации. Определяем, какой
- 17. Для оценки тесноты связи по результатам факторной
- 18. Для характеристики тесноты корреляционной связи между признаками
- 19. Подобные операции выполняют и с корреляционным отношением
- 20. Если факторный признак не влияет на результативный,
- 21. Дисперсионный анализ позволяет не только определить роль
- 22. Для оценки существенности корреляционного отношения пользуются критическими
- 23. Уровень значимости – это достаточно малое
- 24. Слайд 24
- 25. Этот показатель всегда рассчитывается по выборочным данным,
- 26. Критерий Фишера Фишер составил таблицы, по которым
- 27. Особенности корреляционно-регрессионных связейКорреляционная связь проявляется, когда одному
- 28. При корреляционной связи имеет место не изменение
- 29. Корреляционно-регрессионный позволяет решить две задачи: определение формы связи; измерение тесноты связи.
- 30. Первая задача заключается в определении формы связи,
- 31. Вторая задача состоит в измерении тесноты, т.
- 32. Этапы корреляционного анализа:1) предварительный анализ объекта исследования;
- 33. Виды корреляционно-регрессионных связейпрямой связи с увеличением аргумента
- 34. Кроме того, в виде исключений, которые, однако,
- 35. По аналитическому выражению уравнение регрессии может быть
- 36. Прямолинейная зависимость в этом случае может быть
- 37. Если происходит неравномерное изменение явления в связи
- 38. характеризует степень ускорения или замедления кривизны
- 39. Уравнение криволинейной связи может быть выражено и в виде гиперболической функции
- 40. Аналитическое выражение связи.Аналитические методы – основной способ
- 41. Измерение тесноты связи Для измерения тесноты прямолинейной
- 42. Слайд 42
- 43. Коэффициент корреляции rxy применяется только в тех
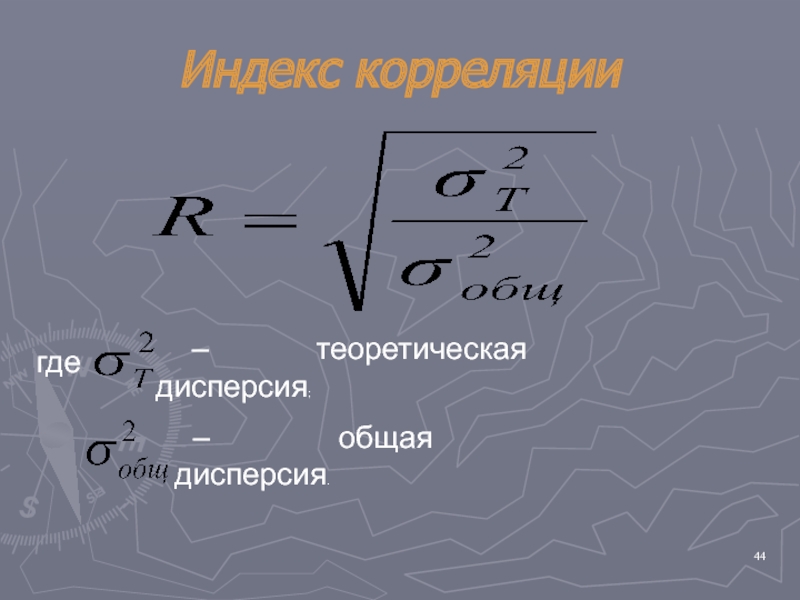
- 44. Индекс корреляциигде – теоретическая дисперсия; – общая дисперсия.
- 45. Коэффициент корреляции является мерой тесноты связи только
- 46. Коэффициент (индекс) детерминации Этот показатель универсален: может
- 47. Множественная корреляция Множественная корреляция занимается изучением, измерении
- 48. Множественная корреляция определяет:1) форму связи; 2)
- 49. Определение формы связи сводится обычно к отысканию
- 50. Для определения параметров a0, a1 и a2
- 51. Измерение тесноты связиПосле получения коэффициентов регрессии нужно
- 52. Правило сложения дисперсий
- 53. Теоретическая дисперсия теоретическая дисперсия – это вариация теоретического признака вокруг общей средней
- 54. Остаточная дисперсия Остаточная дисперсия – это среднее квадратическое отклонение теоретического признака от фактического.
- 55. Коэффициент множественной корреляции где rxy, rzy, rxz – парные коэффициенты корреляции
- 56. Частных коэффициентов корреляции
- 57. Скачать презентанцию
Виды и формы связи между явлениями Взаимосвязанные признаки подразделяются на факторные (под их воздействием изменяются другие, зависящие от них признаки) и результативные.
Слайды и текст этой презентации
Слайд 2 Виды и формы связи между явлениями
Взаимосвязанные признаки подразделяются
на факторные (под их воздействием изменяются другие, зависящие от них
признаки) и результативные.
Слайд 3Функциональная связь
При функциональной связи каждому значению факторного признака соответствует строго
определенное одно или несколько значений результативного признака; для выявления такой
связи достаточно одного наблюдения. Она полностью сохраняет свою силу и проявляется во всех случаях наблюдения и для всех единиц наблюдения. Функциональные связи иначе называются полными
Слайд 4Стохастическая связь
Связь между случайными величинами называется стохастической. Частный случай стохастической
связи – статистические связи. Статистические связи подразделяются на корреляционные и
регрессионные. Корреляционные связи отражают зависимость между случайными величинами, а регрессионные – между случайными и неслучайными.
Слайд 5При статистической связи одному и тому же значению факторного признака
может соответствовать несколько значений результативного признака. Особенность статистических закономерностей состоит
в том, что строгую функциональную зависимость между явлениями выявить нельзя. Статистические закономерности проявляются только для большого числа единиц совокупности, а динамические проявляются у каждой отдельной единицы.
Слайд 6Основные приемы изучения взаимосвязей
Для изучения, измерения и количественного выражения
взаимосвязей между явлениями применяются различные методы. Важнейшие из них: метод
сопоставления параллельных рядов, балансовый, графический, методы аналитических группировок, дисперсионного и корреляционного анализа. Наибольший эффект достигается при комбинировании нескольких методов.
Слайд 7Метод сравнения параллельных рядов
Приводится ряд данных по одному признаку и
параллельно с ним по другому признаку, связь с которым предполагается.
По вариации признака в первом и втором ряду судят о наличии связи признаков. Такой метод позволяет вывести только направление связи, но не измерить ее.
Слайд 8Пример: Предположим, нужно выяснить, есть ли зависимость между объемом производства
на предприятии и себестоимостью. Берем предприятия и ранжируем их по
объему выпуска (по возрастанию), и смотрим, возрастает или уменьшается при этом себестоимость.
Слайд 9Балансовый метод состоит в том, что данные взаимосвязанных показателей изображаются
в виде таблицы и располагаются таким образом, чтобы итоги между
отдельными ее частями были равны, т. е., чтобы был баланс. Балансовый метод используется для характеристики взаимосвязи между производством и распределением продуктов, денежными доходами и расходами населения. Почти все внутренние и внешние хозяйственные связи выражаются в виде балансов.
Слайд 11Графический метод может использоваться как самостоятельно, так и совместно с
другими методами.
Если конкретные данные перенести на график,
то получим поле точек. На оси абсцисс откладываются значения факторного признака x, а на оси ординат – значения результативного признака y. Каждая единица, обладающая определенным значением факторного и результативного признака, обозначается точкой. По совместному расположению точек на графике делают вывод о направлении и наличии зависимости 
Слайд 12Беспорядочное расположение говорит об отсутствии связи. Напротив, чем сильнее связь,
тем теснее точки группируются вокруг определенной линии. Если точки на
графике концентрируются вокруг прямой, идущей снизу вверх, зависимость между признаками прямая. Если точки концентрируются вокруг прямой, спускающейся сверху вниз, то это свидетельствует о наличии обратной зависимости.
Слайд 13Метод аналитической группировки
Единицы статистической совокупности группируются, как правило, по факторному
признаку и для каждой группы рассчитывается средняя или относительная величина
по результативному признаку. Затем изменения средних или относительных значений результативного признака сопоставляются с изменениями факторного признака для выявления характера связи между ними. Сначала выбираются два признака: факторный и результативный. По факторному признаку производится группировка, а по результативному – подсчет средних или относительных величин. Путем сопоставления характера изменений значений факторного и результативного признака можно сделать вывод о наличии связи и ее направлении. При помощи метода аналитической группировки можно сделать вывод и о тесноте связи.
Слайд 14Пример : Количество вкладчиков и средний остаток вклада по трем
филиалам Сбербанка (тыс. руб.)*.
Слайд 15Дисперсионный анализ дает прежде всего возможность определить значение систематической и
случайной вариаций в общей вариации, а также установить роль интересующего
нас фактора в изменении результативного признака.
Слайд 16
Анализ проходит четыре итерации.
Определяем, какой признак факторный, какой – результативный.
Производим группировку по факторному признаку.
Считаем среднее значение факторного и
результативного признака в группах. Выясняем взаимосвязь между этими средними.
Слайд 17Для оценки тесноты связи по результатам факторной группировки используется межгрупповая
дисперсия . Напомним, что межгрупповая дисперсия характеризует колеблемость групповых средних
вокруг общей средней, которая возникает под действием факторов, положенных в основу группировки. Если при этом групповая средняя равна средней общей, значит, фактор, положенный в основу группировки, на результативный признак не влияет.
Слайд 18Для характеристики тесноты корреляционной связи между признаками в аналитических группировках
межгрупповую дисперсию сопоставляют с общей. Это сопоставление называется коэффициентом детерминации
. Он показывает, какая часть общей дисперсии связана с факторами, положенными в основу группировки.
Слайд 19Подобные операции выполняют и с корреляционным отношением . Оно характеризует
долю вариации результативного признака, вызванной действием факторного признака, положенного в
основание группировки. Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем большее влияние оказывает факторный признак на результативный.
Слайд 20Если факторный признак не влияет на результативный, то вариация, обусловленная
им, будет равна нулю (δ2 = 0); корреляционное отношение также
равно нулю (η = 0), что говорит о полном отсутствии связи. Напротив, если результативный признак изменяется только под воздействием одного факторного признака, то вариация, обусловленная этим признаком, будет равна общей вариации (δ2 = σ2) и корреляционное отношение будет равно единице (η = 1), что говорит о существовании полной связи.
Слайд 21Дисперсионный анализ позволяет не только определить роль случайной и систематической
вариаций в общей вариации, но и оценить достоверность вариации, обнаруженной
методом аналитических группировок. Определение достоверности вариации дает возможность с заданной степенью вероятности установить, вызвана ли межгрупповая вариация признаком, положенным в основание группировки, или она является результатом действия случайных причин.
Слайд 22Для оценки существенности корреляционного отношения пользуются критическими значениями корреляционного отношения
η при разных уровнях вероятности или значимости α.
Слайд 23 Уровень значимости – это достаточно малое значение вероятности, отвечающее
событиям, которые в данных условиях исследования будут считаться практически невозможными.
Появление такого события считается указанием на неправильность начального предположения. Чаще всего пользуются уровнями, равными 0,05 или 0,01.
Слайд 24
k1 = m –
1,где m – число групп,
для случайной дисперсии
k2 = n – m,
где n – число вариант,
m – число групп.
Слайд 25Этот показатель всегда рассчитывается по выборочным данным, и потому может
быть ситуация, когда данное значение получилось случайно. Чтобы исключить случайности,
проводят проверку достоверности. Для этого можно рассчитать критерий Фишера.
Слайд 26Критерий Фишера
Фишер составил таблицы, по которым можно определить значения
критерия. Если мы получаем значение F, большее, чем значение в
таблице, то рассчитываемое значение получилось неслучайно (с вероятностью 99% или 95%, в зависимости от того, какую таблицу мы взяли). Критерий Фишера можно использовать только тогда, когда распределение близко к нормальному
Слайд 27Особенности корреляционно-регрессионных связей
Корреляционная связь проявляется, когда одному и тому же
значению факторного признака соответствует ряд значений признака-результата, причем связь обнаруживается
в виде тенденции изменения среднего значения результативного признака в зависимости от изменения факторного признака. Это свободная и неполная связь.
Слайд 28При корреляционной связи имеет место не изменение функции в зависимости
от изменения аргумента, а имеет место вариация результативного признака вокруг
его среднего значения в зависимости от изменения факторного признака. Вот почему корреляционная связь является не строгой. Кроме того, как правило, корреляционные зависимости являются не полными: мы не знаем всех факторов и их воздействия.
Слайд 29Корреляционно-регрессионный позволяет решить две задачи:
определение формы связи;
измерение тесноты связи.
Слайд 30Первая задача заключается в определении формы связи, так как от
этого зависит конечный результат изучения взаимосвязи между признаками. Первая задача
решается путем нахождения уравнения регрессии.
Слайд 31Вторая задача состоит в измерении тесноты, т. е. меры связи
между признаками с целью установить степень влияния данного фактора на
результат и оценки степени влияния неучтенных факторов.
Слайд 32Этапы корреляционного анализа:
1) предварительный анализ объекта исследования;
2) сбор и
первичная обработка информации;
3) построение уравнения регрессии и определение его параметров;
4) проверка адекватности полученной модели.
Слайд 33Виды корреляционно-регрессионных связей
прямой связи с увеличением аргумента х функция у
также увеличивается без всяких единичных исключений.
обратной связи увеличение факторного
признака х сопровождается уменьшением результативного признака у без всяких единичных исключений. 
Слайд 34Кроме того, в виде исключений, которые, однако, не нарушают общей
тенденции, встречается частичная связь – прямая или обратная. Когда признаки
варьируют независимо друг от друга, говорят о полном отсутствии связи.
Слайд 35По аналитическому выражению уравнение регрессии может быть прямолинейным и криволинейным.
Прямолинейное уравнение регрессии характеризуется тем, что величина явления изменяется приблизительно
равномерно в соответствии с изменением величины влияющего фактора.
Слайд 36Прямолинейная зависимость в этом случае может быть выражена уравнением прямой:
Параметр
называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина
результативного признака y при отклонении величины факторного признака x на одну единицу.
Слайд 37Если происходит неравномерное изменение явления в связи с изменением величины
влияющего фактора, то такая связь называется криволинейной. Математически криволинейная зависимость
может быть выражена уравнением криволинейной связи. В экономическом анализе для ее выражения часто пользуются уравнением параболы второго порядка:
Слайд 38
характеризует степень ускорения или замедления кривизны параболы
>
0 парабола имеет минимум,
< 0 – максимум.
характеризует
угол наклона кривой, – начало кривой.
Слайд 40Аналитическое выражение связи.
Аналитические методы – основной способ изучения связи. Они
делятся на непараметрические и параметрические. Применение методов корреляционного анализа дает
возможность выражать связь между признаками аналитически (в виде уравнения) и придавать ей количественное выражение.
Слайд 41Измерение тесноты связи
Для измерения тесноты прямолинейной связи между двумя признаками
используется линейный коэффициент корреляции, который обозначается rxy
Слайд 43Коэффициент корреляции rxy применяется только в тех случаях, когда между
явлениями существует прямолинейная связь. Если же связь криволинейная, то пользуются
индексом корреляции, оценивающим тесноту связи
Слайд 45Коэффициент корреляции является мерой тесноты связи только для линейной формы
связи, а индекс корреляции – и для линейной, и для
криволинейной. При прямолинейной связи коэффициент корреляции по своей абсолютной величине равен индексу корреляции.
Слайд 46Коэффициент (индекс) детерминации
Этот показатель универсален: может использоваться при любом
количестве факторных признаков, при любой форме связи. Он показывает, какая
часть общей дисперсии результативного признака определяется факторами, включенными в уравнение регрессии.
Слайд 47Множественная корреляция
Множественная корреляция занимается изучением, измерении связи между результативным
признаком, двумя и более факторными.
Слайд 48Множественная корреляция определяет:
1) форму связи;
2) тесноту связи;
3) влияние отдельных факторов на общий результат.
Слайд 49Определение формы связи сводится обычно к отысканию уравнения связи у
с факторами х, z, ω, ..., ν. Так, линейное уравнение
зависимости результативного признака от двух факторных определяется по формуле:Yxz=a0 + a1x + a2z
Слайд 50Для определения параметров a0, a1 и a2 по способу наименьших
квадратов необходимо решить следующую систему трех нормальных уравнений:
Слайд 51Измерение тесноты связи
После получения коэффициентов регрессии нужно измерить тесноту связи
между факторными и результативным признаками для полученной модели. Измерение тесноты
производится на основе вариации результативного признака и правила сложения дисперсий.
Слайд 53Теоретическая дисперсия
теоретическая дисперсия – это вариация теоретического признака вокруг
общей средней
Слайд 54Остаточная дисперсия
Остаточная дисперсия – это среднее квадратическое отклонение теоретического
признака от фактического.
