Слайд 1Лекция 5
Тесты проверки предпосылок теоремы Гаусса-Маркова
Слайд 2Методика проверки статистических гипотез
Определение. Под статистической гипотезой понимается любое предположение
о виде закона распределения случайной величины или значениях его параметров.
Примеры
статистических гипотез:
Н0:(U имеет нормальный закон распределения).
H0:(параметр а0=0)
Н1:(параметр а0=1)
Гипотезы H0 и H1 называются основной и альтернативной.
Слайд 3Методика проверки статистических гипотез
Алгоритм проверки статистических гипотез.
Формулируется статистическая гипотеза H0.
Искусственно
формируется случайная величина «Z», закон распределения которой известен [Pz(t,a1, a2)],
котoрая тесно связана с гипотезой.
Область допустимых значений Z делится на две части: Ω0 в которой гипотеза принимается и, Ω в которой она отклоняется. Граница этих областей определяется из условия, что Z попадает в область Ω0 с заданной вероятностью «р».
По данным выборки вычисляется значение случайной величины Z и проверяется ее принадлежность область Ω0.
Слайд 4Методика проверки статистических гипотез
Примеры. В схеме Гаусса-Маркова случайные переменные:
называются дробью
Стьюдента и подчиняются закону распределения Стьюдента. Критическое значение дроби Стьюдента
находится из уравнения:
Здесь: Pt(q) функция плотности вероятности распределения Стьюдента, tкр – двусторонняя квантиль распределения.
Рдов- значение доверительной вероятности, Рдов=0.95/0.99
Слайд 5Методика проверки статистических гипотез
В схеме Гаусса-Маркова переменная:
подчиняется закону распределения
Фишера
Слайд 6Методика проверки статистических гипотез
Возможные ошибки при проверке статистических гипотез.
Ошибка первого
рода.
Когда справедливая гипотеза отклоняется.
Ошибка второго рода.
Когда ложная гипотеза принимается.
Слайд 7 Модель: Y = b1 + b2X + u
Нулевая гипотеза:
Альтернативная гипотеза:
Проверка нулевой гипотезы, что 2 = 20 или
альтернативной гипотезы
Пример модели: Темпы общей инфляции в зависимости
от темпов роста заработной платы.
p = b1 + b2w + u
Нулевая гипотеза:
Альтернативная гипотеза:
4
ПРОВЕРКА ГИПОТЕЗ
СВЯЗАННЫХ С КОЭФФИЦИЕНТАМИ РЕГРЕССИИ
Слайд 8
6
ПРОВЕРКА ГИПОТЕЗ
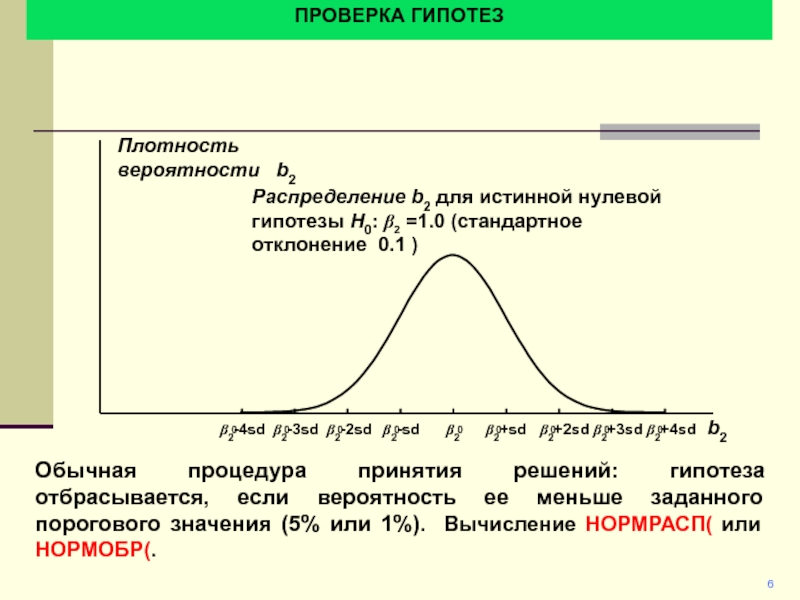
Плотность вероятности b2
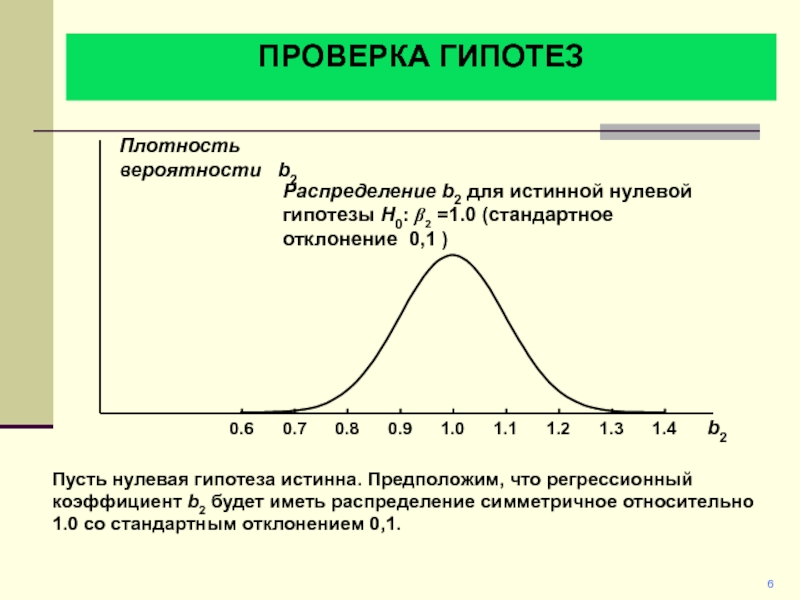
Распределение b2 для истинной нулевой гипотезы
H0: b2 =1.0 (стандартное отклонение 0,1 )
b2
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
Пусть нулевая гипотеза истинна.
Предположим, что регрессионный коэффициент b2 будет иметь распределение симметричное относительно 1.0 со стандартным отклонением 0,1.
Слайд 9
6
ПРОВЕРКА ГИПОТЕЗ
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы
H0: b2 =1.0 (стандартное отклонение 0.1 )
b2
Предположим, что стандартное отклонение
(sd) известно.
Слайд 10
9
ПРОВЕРКА ГИПОТЕЗ
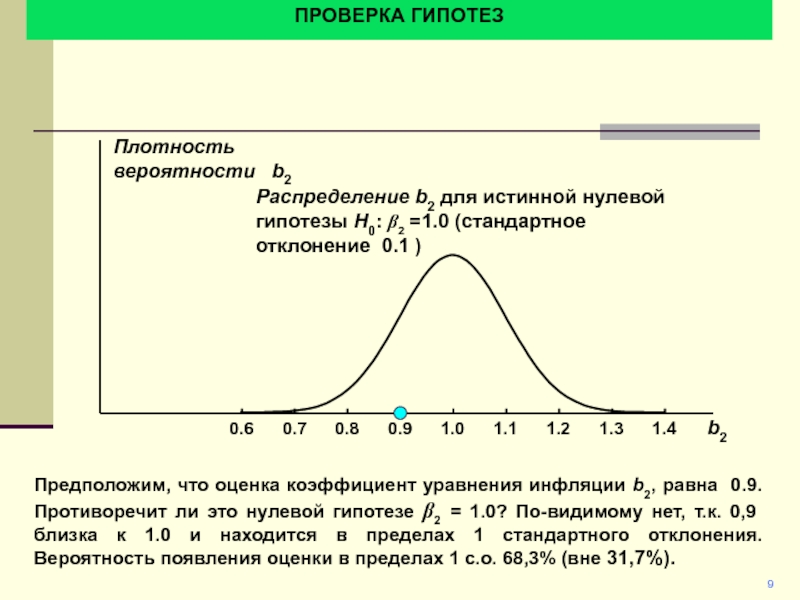
Предположим, что оценка коэффициент уравнения инфляции b2, равна 0.9.
Противоречит ли это нулевой гипотезе b2 = 1.0? По-видимому нет,
т.к. 0,9 близка к 1.0 и находится в пределах 1 стандартного отклонения. Вероятность появления оценки в пределах 1 с.о. 68,3% (вне 31,7%).
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 11
14
ПРОВЕРКА ГИПОТЕЗ
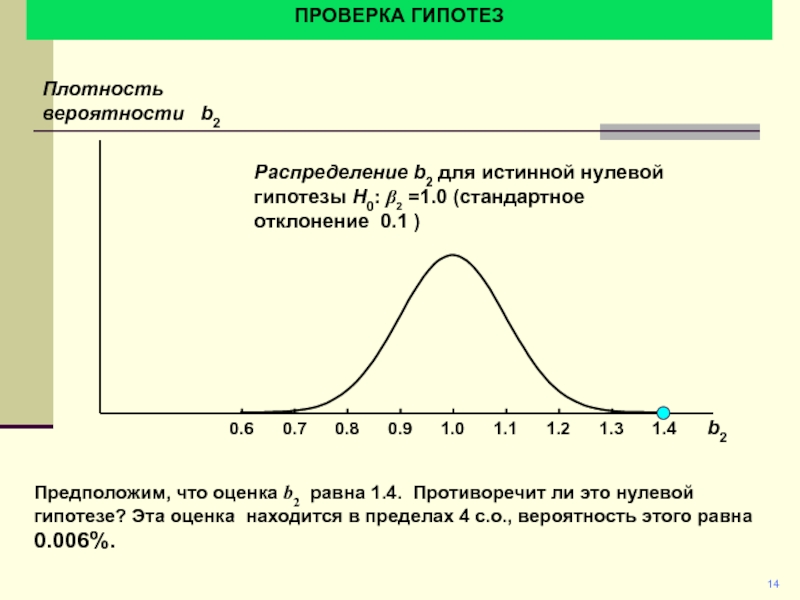
Предположим, что оценка b2 равна 1.4. Противоречит ли это
нулевой гипотезе? Эта оценка находится в пределах 4 с.о., вероятность
этого равна 0.006%.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 12
14
ПРОВЕРКА ГИПОТЕЗ
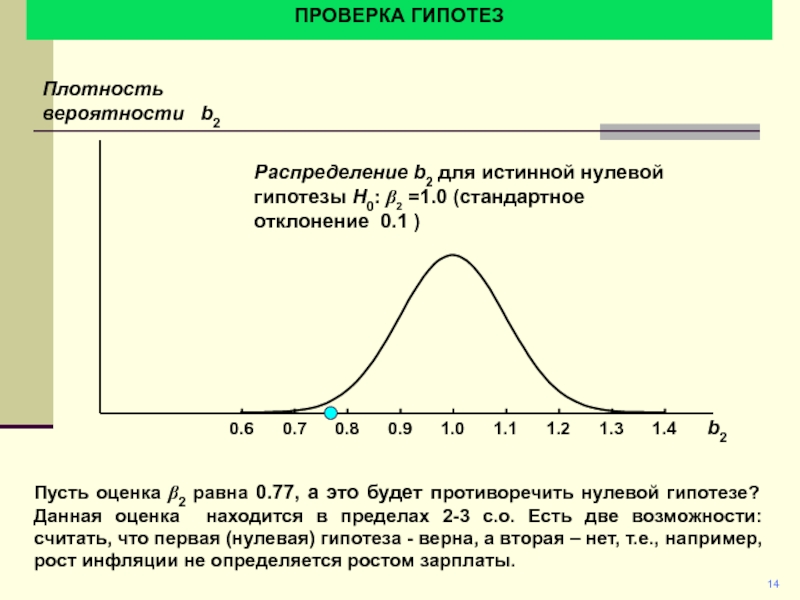
Пусть оценка b2 равна 0.77, а это будет противоречить
нулевой гипотезе? Данная оценка находится в пределах 2-3 с.о. Есть
две возможности: считать, что первая (нулевая) гипотеза - верна, а вторая – нет, т.е., например, рост инфляции не определяется ростом зарплаты.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 13
6
ПРОВЕРКА ГИПОТЕЗ
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы
H0: b2 =1.0 (стандартное отклонение 0.1 )
b2
Обычная процедура принятия решений:
гипотеза отбрасывается, если вероятность ее меньше заданного порогового значения (5% или 1%). Вычисление НОРМРАСП( или НОРМОБР(.
Слайд 14
21
ПРОВЕРКА ГИПОТЕЗ
Например, можно предположить, что гипотеза отбрасывается при пороге вероятности
меньшим чем 0.05 (5%). 2.5% хвосты – это 1,96 стандартного
отклонения (с.о.).
2.5%
2.5%
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 152.5%
2.5%
23
ПРОВЕРКА ГИПОТЕЗ
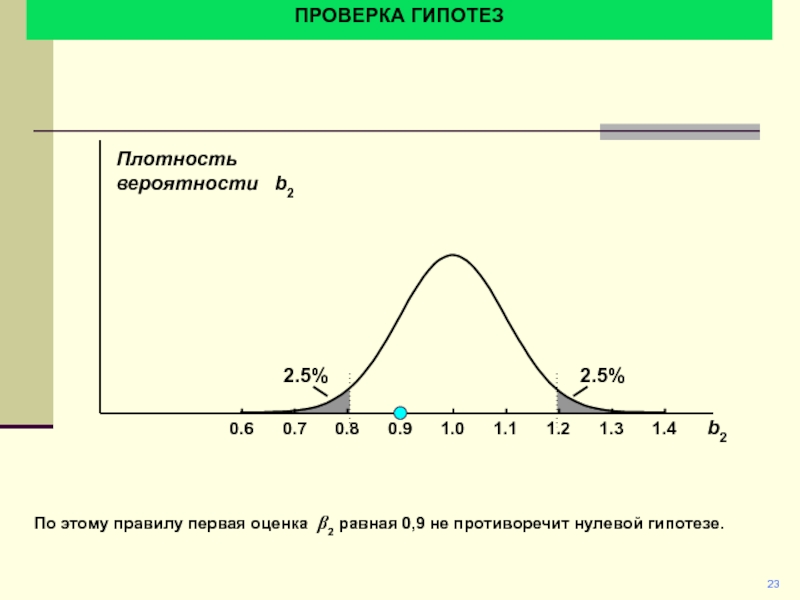
По этому правилу первая оценка b2 равная 0,9
не противоречит нулевой гипотезе.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Слайд 162.5%
2.5%
23
ПРОВЕРКА ГИПОТЕЗ
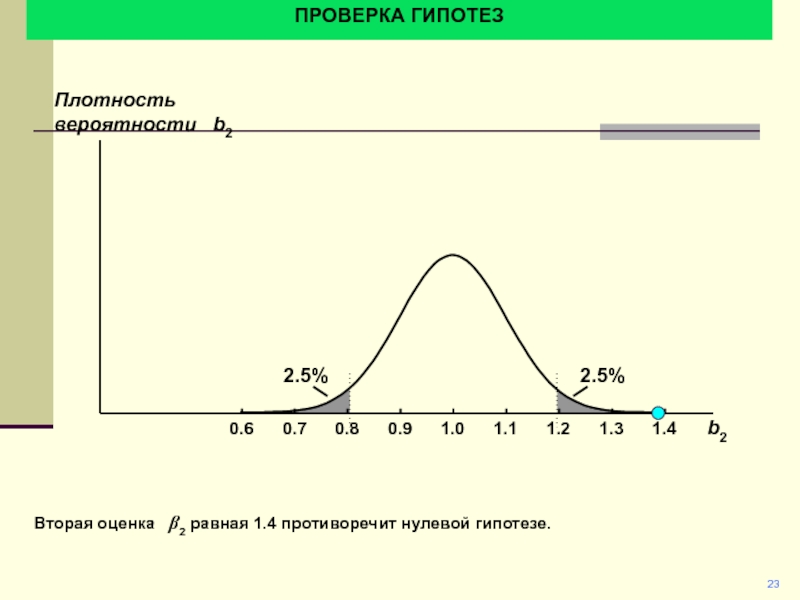
Вторая оценка b2 равная 1.4 противоречит нулевой
гипотезе.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Слайд 172.5%
2.5%
23
ПРОВЕРКА ГИПОТЕЗ
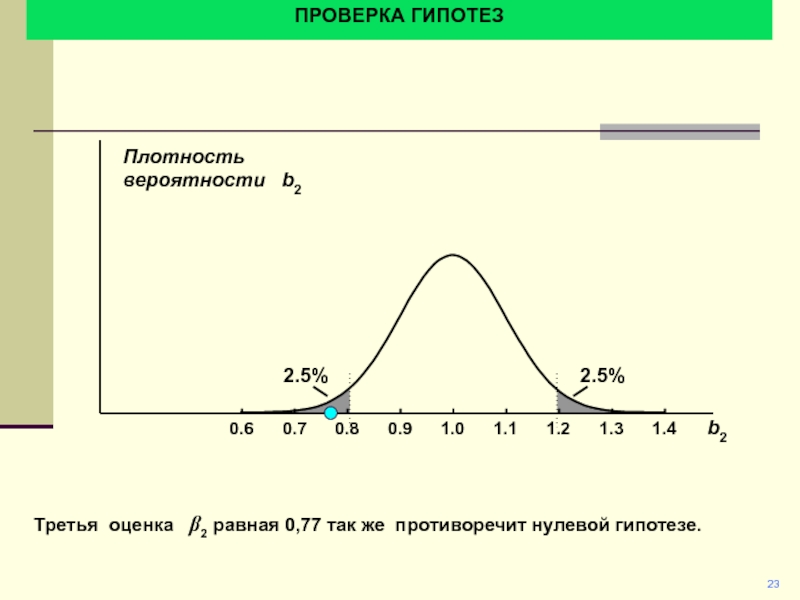
Третья оценка b2 равная 0,77 так же
противоречит нулевой гипотезе.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Слайд 18
ПРОВЕРКА ГИПОТЕЗ
2.5%
2.5%
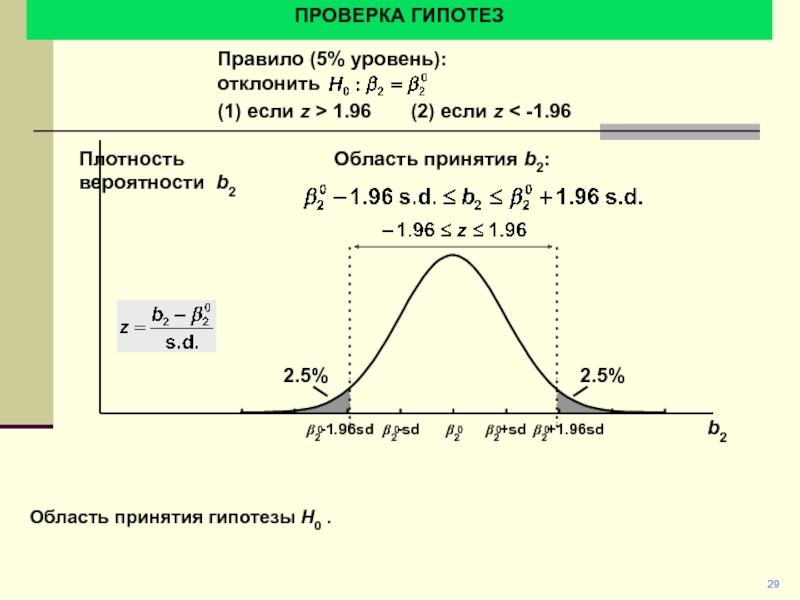
Правило (5% уровень):
отклонить
(1) если (2) если
(1)
если (2) если
(1) если
(2) если
(1) если z > 1.96 (2) если z < -1.96
Плотность вероятности b2
b2
H0 отклоняется если значение оценки больше 1.96 (положительное или отрицательное).
29
Слайд 19
ПРОВЕРКА ГИПОТЕЗ
2.5%
2.5%
Правило (5% уровень):
отклонить
(1) если z > 1.96
(2) если z < -1.96
Плотность вероятности b2
b2
Область принятия гипотезы
H0 .
29
Область принятия b2:
Слайд 202.5%
2.5%
36
ПРОВЕРКА ГИПОТЕЗ
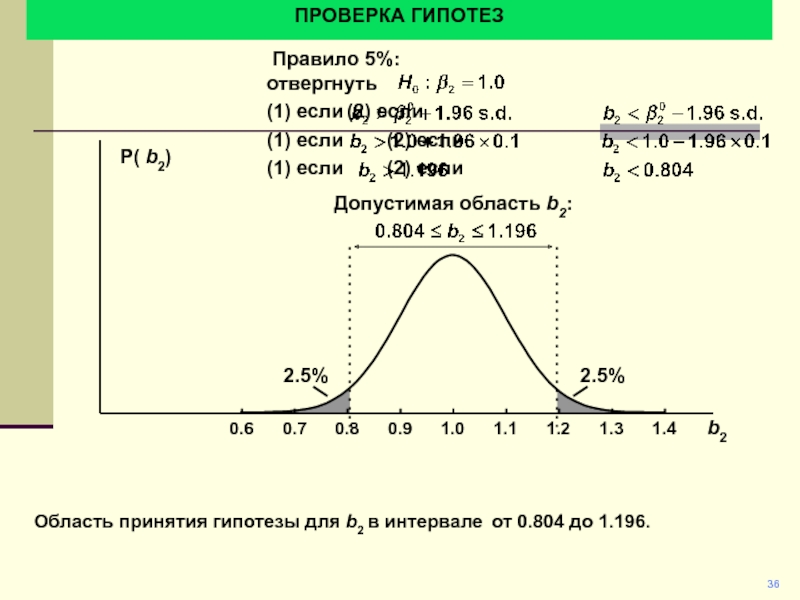
Область принятия гипотезы для b2 в интервале от 0.804
до 1.196.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
Р( b2)
b2
Правило 5%:
отвергнуть
(1) если (2) если
(1) если
(2) если
(1) если (2) если
Допустимая область b2:
Слайд 21
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
R2 – мера качества объяснения регрессионным уравнением
закономерности. Нулевая гипотеза для тестирования заключается в том, что модель
не имеет объяснительной силы.
4
Слайд 22
9
Для оценки качества R2 можно использовать F – статистику (распределение
Фишера). k- число степеней свободы (количество объясняющих переменных и свободный
коэффициент), n - число экспериментов.
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
Слайд 23
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
Легко показать, что RSS/TSS равно 1
- R2. F монотонная функция R2. С увеличением R2 увеличивается
и F , k – число параметров в регрессии
10
Слайд 24
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
По Fcrit можно вычислить Rcrit .
19
Слайд 25
Гомоскедастичность
и
Гетероскедастичность случайных возмущений
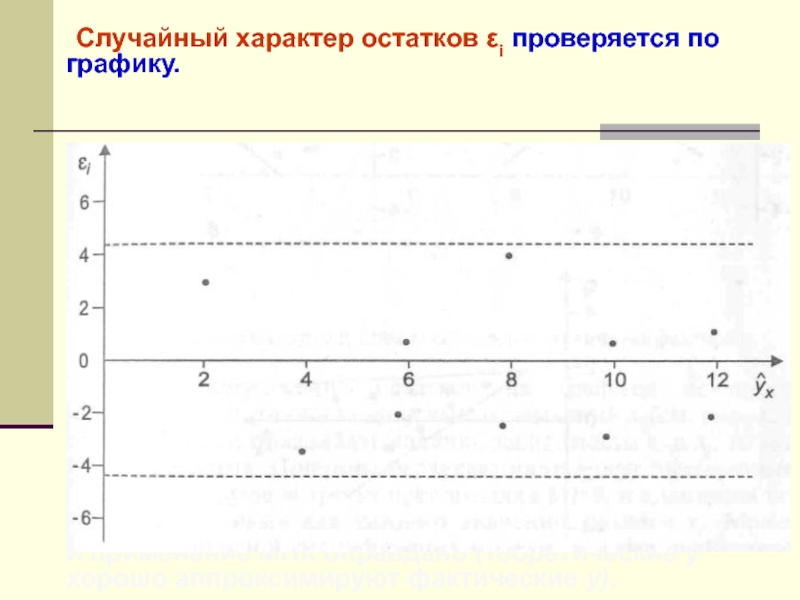
Слайд 26 Случайный характер остатков εi проверяется по графику.
Если
на графике нет направленности в расположении точек εi , то
εi – случайные величины и применение МНК оправдано (теоретические y хорошо аппроксимируют фактические y).
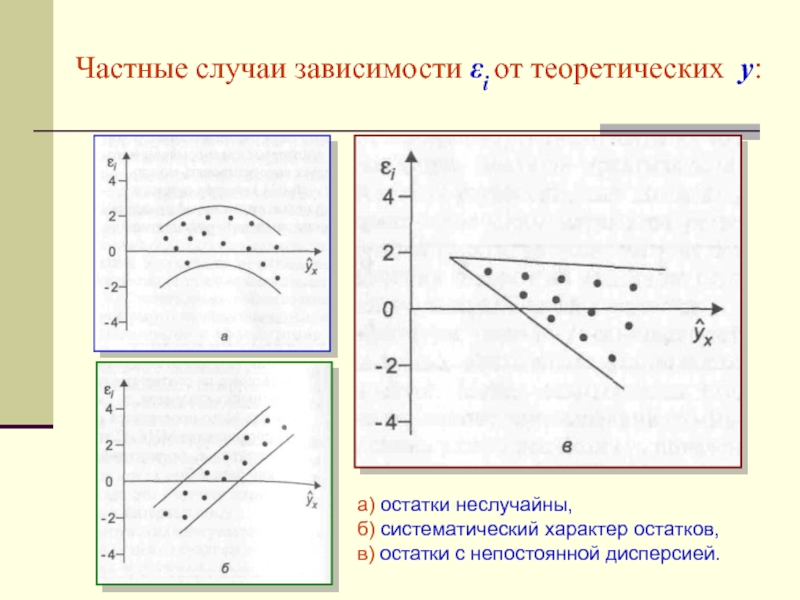
Слайд 27Частные случаи зависимости εi от теоретических y:
а) остатки неслучайны,
б)
систематический характер остатков, в) остатки с непостоянной дисперсией.
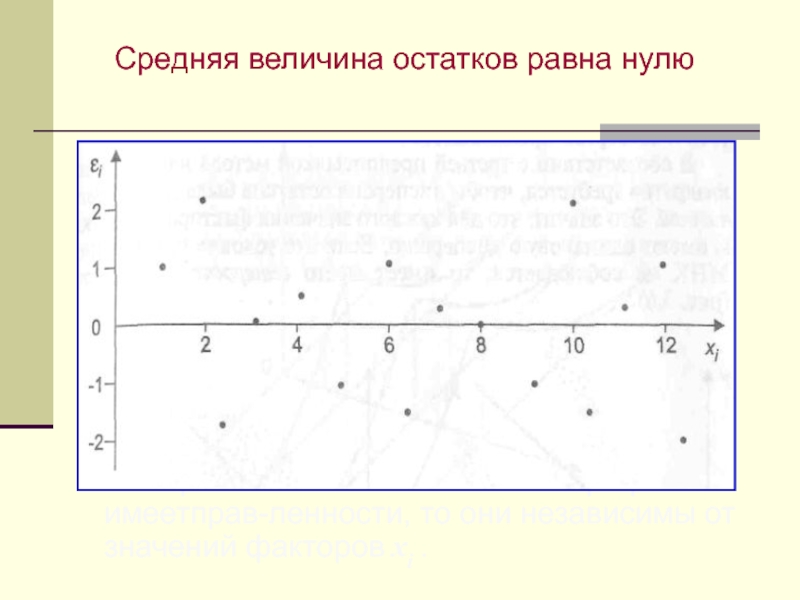
Слайд 28Средняя величина остатков равна нулю
Если расположение остатков на
графике не имеетправ-ленности, то они независимы от значений факторов xi
.
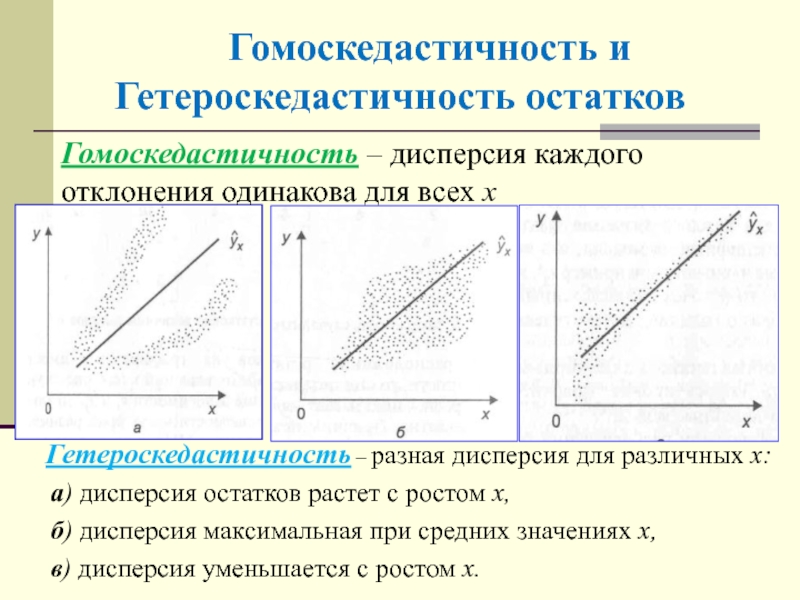
Слайд 29 Гомоскедастичность и Гетероскедастичность остатков
Гетероскедастичность – разная дисперсия
для различных x:
а) дисперсия остатков растет с ростом x,
б)
дисперсия максимальная при средних значениях x,
в) дисперсия уменьшается с ростом x.
Гомоскедастичность – дисперсия каждого отклонения одинакова для всех x
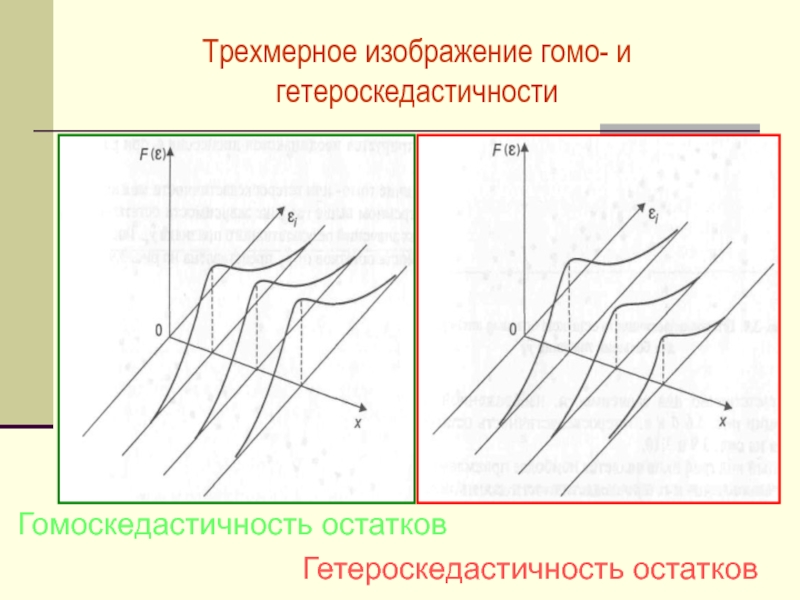
Слайд 30Трехмерное изображение гомо- и гетероскедастичности
Гомоскедастичность остатков
Гетероскедастичность остатков
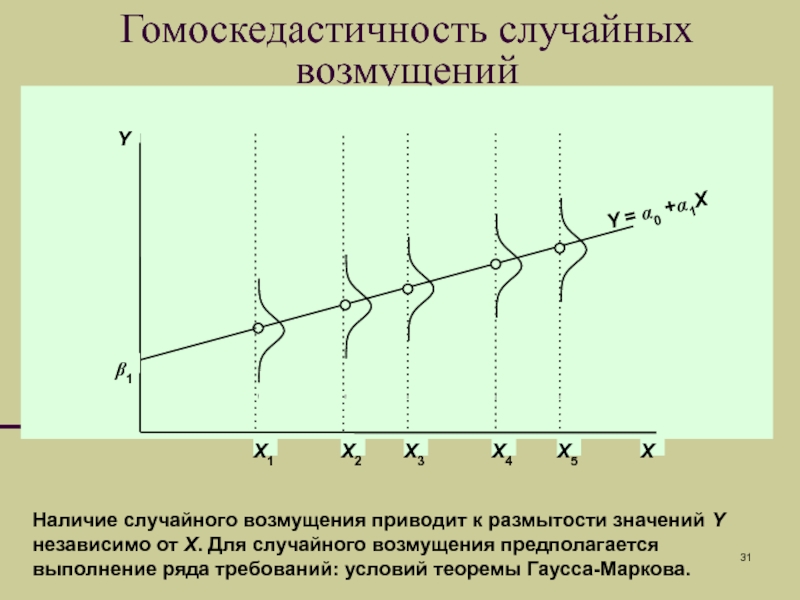
Слайд 31Гомоскедастичность случайных возмущений
b1
X
Y = a0 +a1X
Y
Наличие случайного возмущения приводит к
размытости значений Y независимо от X. Для случайного возмущения предполагается
выполнение ряда требований: условий теоремы Гаусса-Маркова.
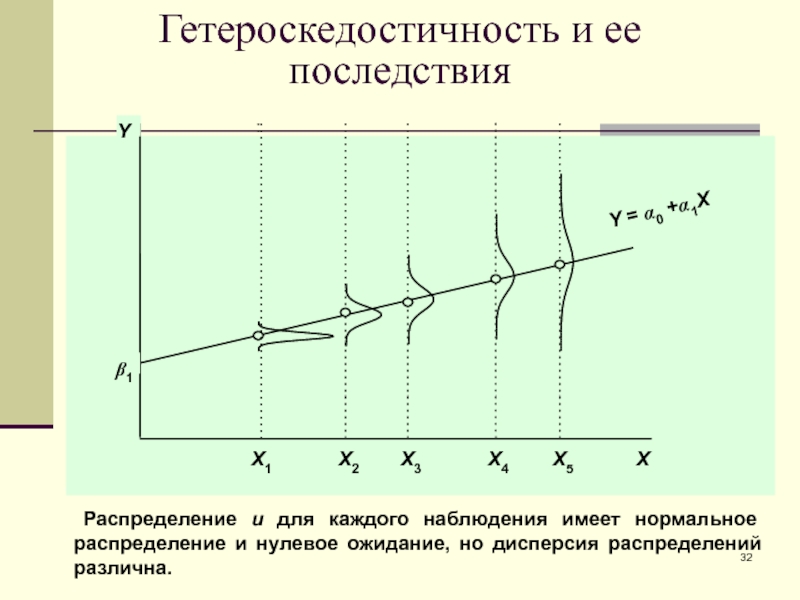
Слайд 32Гетероскедостичность и ее последствия
b1
X
Y = a0 +a1X
Y
Распределение u для
каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия
распределений различна.
Слайд 33Гетероскедостичность и ее последствия
Условия обеспечивающие гомоскедастичность
(однородность) случайных возмущений:
1. Нормальное
распределение случайных возмущений для всех наблюдений.
2. Средние значения случайных возмущений
в каждом наблюдении равно нулю.
3. Распределения одинаковы для всех наблюдений.
Последствия нарушения условия гомоскедастичности случайных возмущений:
1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от МНК и более эффективные оценки.
2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки.
Слайд 34Гетероскедостичность и ее последствия
В связи с тем, что оценка всех
параметров модели, включая вид параметры закона распределения случайного возмущения, проводится
по результатам случайной выборки, то справедливо говорить только о статистических гипотезах относительно выполнения предпосылок теоремы Гаусса-Маркова.
Определим, как производится проверка статистических гипотез.
Слайд 35 Обнаружение гетероскедастичности
Гетероскедастичность можно выявить тремя тестами:
-
тест Голдфельда-Квандта (применяется при малом объеме выборки, нормальном распределении ε
и дисперсии остатков пропорциональной квадрату фактора);
- тест ранговой корреляции Спирмена;
- тест Глейзера.
Слайд 36ТесТ
ГолдФелда-квандта
Лекция 5. Часть 2
Слайд 37Тест Голдфелда-Квандта
Данный тест предназначен для того, чтобы проверить гипотезу
об отсутствии гетероскедастичности случайных возмущений в схеме Гаусса-Маркова.
Случай уравнения парной регрессии.
Имеем спецификацию модели в виде:
Yt=a0 + a1xt+ut
Имеем выборку в объеме n наблюдений с переменными Yt и xt для оценки параметров модели.
Задача: проверить гипотезу об отсутствии гетероскедастичности в полученной модели.
Слайд 38Тест Голдфелда-Квандта
В основе теста лежат два предположения.
Случайные возмущения подчиняются нормальному
закону распределения.
Стандартные ошибки случайных возмущений σ(ut) пропорциональны значениям регрессора xt.
Слайд 39Алгоритм применения теста Голдфелда-Квандта
Шаг 1. Имеющаяся выборка из n наблюдений
сортируется (ранжируется) по возрастанию значений регрессора х.
Шаг 2. Полученная в
результате сортировки выборка делится на три примерно равные части (при малых объемах можно на 2 равные части).
Шаг 3. Для первой и третьей частей выборки строятся модели парной регрессии, т.е. для них вычисляются оценки параметров a0 и a1.
В результате получаются две модели парной регрессии (для каждой части общей выборки):
Y1=ã01 + ã11x +u1 (5.1)
Y3=ã03 + ã13x +u3 (5.2)
Исходя из принятых допущений, считается, что, если ошибки случайных возмущений в «первой» и «третьей» частях выборки будут равны, то условие гомоскедостичности выполняется.
Слайд 40Алгоритм применения теста Голдфелда-Квандта
Шаг 4. Для уравнений (5.1) и (5.2)
вычисляются значения RSS1 (ESS1) и RSS 3 (ESS3) - остаточные
суммы квадратов каждой из регрессий:
Где ESS(RSS) =Σ(ui2)=Σ(yi-ã0-ã1xi)2
Шаг 5. Проверяется гипотеза о равенстве σu1 и σu3.
Формируется случайная переменная GQ в виде:
В схеме Гаусса-Маркова переменная GQ имеет закон распределения Фишера.
Слайд 41Алгоритм применения теста Голдфелда-Квандта
Вычисленное значение GQ сравнивается с
критическим значением
Fкр(Pдов,n1,n3):
Если
GQ ≤ Fкр(Pдов,n1,n3)
и 1/GQ ≤ Fкр(Pдов,n1,n3),
то гипотеза о гомоскедастичности случайных возмущений принимается.
Случай уравнения множественной регрессии.
Yt=a0+a1x1t+a2x2t+a3x3t+ut
Сортировка проводится по величине z=|x1|+|x2|+|x3|.
Если тест дает отрицательный результат, алгоритм повторяется для каждого регрессора.
В результате обнаруживается регрессор вызывающий гетероскедастичность.
Слайд 42тест ранговой корреляции
Спирмена
Слайд 43Тест ранговой корреляции Спирмена
Это тест на гетероскедастичность, устанавливающий, что
стандартное отклонение остаточного члена регрессии имеет нестрогую линейную зависимость с
объясняющей переменной.
Тест основан на вычислении коэффициента ранговой корреляции между значениями остатков регрессии (u) и значениями фактора - регрессора (x). При его выполнении предполагается, что дисперсия случайной составляющей будет либо увеличиваться, либо уменьшаться по мере увеличения фактора (x), и поэтому в регрессии, оцениваемой с помощью МНК, абсолютные величины остатков (u) и значения (х) будут коррелированы.
Слайд 44Алгоритм теста ранговой корреляции Спирмена
Шаг 1. Проводится оценка параметров
модели (a0, a1) и значений полученной регрессии (Ŷ), рассчитываются абсолютные
значения остатков (ui)
Шаг 2. Остатки (ui) и значения фактора (xi) ранжируются - определяются их ранги (Dx,, Du) с применением функции РАНГ табличного процессора Excel;
Слайд 45Алгоритм теста ранговой корреляции Спирмена
Шаг 3. Рассчитывается ранговое значение
Di2:
Di2= (Dx – Du)2, а затем определяется значение суммы квадратов
∑Di2 для последующего расчета коэффициента ранговой корреляции Спирмана:
Слайд 46Алгоритм теста ранговой корреляции Спирмена
Шаг 4. Определяется коэффициент ранговой
корреляции Спирмена по формуле:
где n – рассматриваемая выборка данных.
Замечание. Если
среди значений у объясняющего фактора х и объясняемого фактора у встречается несколько одинаковых (образуются связанные ранги), т.е. одинаковые ранговые номера, например, вместо следующего по порядку ранга выдается уже существующий. В этом случае коэффициент Спирмена следует вычислять по следующей формуле
Слайд 47Алгоритм теста ранговой корреляции Спирмена
Шаг 5. Определяется значение tкрит
либо по таблице (см. Таблица), либо по функции СТЬЮДРАСПОБР(α;ν2) в
Excel при заданном уровне значимости α и степеней свободы ν2 = n - 2.
РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
(t-распределение)
Распределение Стьюдента зависит от числа степеней свободы ν2 и уровня значимости (вероятности распределения) α. Например, критическое значение, соответствующее уровню значимости α=0,05, t -распределения с 6 степенями свободы, находится на пересечении столбца 0,05 и строки 6 и будет:
t(0.05,6) = 1.943180.
Доказано, что, если коэффициент корреляции (r) для генеральной совокупности равен нулю, то статистика имеет t-распределение Стьюдента с числом степеней свободы
ν2 = n - 2.
Слайд 48Алгоритм теста ранговой корреляции Спирмена
Шаг 6. Определяется значение статистического
критерия Стьюдента tx,u, и по его величине судят о наличии
или отсутствии гетероскедастичности остатков. Так как
то tx,u будет определяться как:
Слайд 49Алгоритм теста ранговой корреляции Спирмена
Шаг 7. Проводится сравнение полученных
значений tx,u и tкрит. Если выполняется соотношение
, то отклоняется гипотеза о равенстве нулю коэффициента ранговой корреляции, т.е. он признается статистически значимым и принимается гетероскедастичность случайных остатков, а если - то их гомоскедастичность.
Внимание! Если в исследуемой модели имеется более одной объясняющей переменной, то проверка гипотезы об отсутствии гетероскедастичности должна выполняться для каждой из них
Слайд 51Тест Глейзера
Тест основывается на более общих представлениях о зависимости стандартной
ошибки случайной составляющей (σu) от значений объясняющей переменной (х). Предположение
о пропорциональности (σ) и (x) снимаем и хотим проверить, может ли быть более подходящей какая-либо другая функциональная форма, например, когда (σi) рассчитывается по формуле:
(1)
Нулевая гипотеза состоит в равенстве параметра a1= 0 модели (1) (отсутствие гетероскедастичности данного вида). Если при выполнении теста отвергается нулевая гипотеза Н0, то признается гетероскедастичность остатков, а, если нет, то, скорее всего, гетероскедастичности данного вида нет в модели (но это не исключает возможность гетероскедастичности другого вида).
Слайд 52Алгоритм теста Глейзера
Шаг 1. С помощью МНК оценивают параметры регрессии
(y) по (x), рассчитываются значения полученной регрессии (ŷ), а затем
вычисляют абсолютные значения остатков |ui|;
Шаг 2. Для проверки значимости параметра a1 определяется tкрит распределения Стъюдента для задаваемого уровня значимости α и количестве степеней свободы ν1 = n - 2. Если для расчетов применяется табличный процессор Excel, то значение tкрит можно определить, используя функцию СТЬЮДРАСПОБР(α; ν1).
Слайд 53Алгоритм теста Глейзера
Шаг 3. Оцениваются МНК параметры регрессии |ui| по
xγ для нескольких значений γ (от -1,0 до +1,0 с
шагом 0,5):
(1)
Варьирование значений γ от -1 до +1 в уравнении (1) позволяет подобрать наиболее адекватную модель. Для каждого значения проверяется статистическая значимость параметра a1 с помощью критерия Стьюдента, полученного на шаге 2, или эквивалентного ему F-теста на значимость вспомогательной регрессии в целом.
Если для некоторых параметр a1 признается значимым (тестовая статистика больше критического значения), то гетероскедастичность данного вида признается значимой.
Слайд 54Алгоритм теста Глейзера
Среди всех анализируемых моделей выбирается модель с тем
значением , для которого параметр a1 наиболее значим (с наибольшим
значением тестовой статистики).
Если Н0: a1 = 0 не отклоняется (т.е. a1 не значим), то принимается гипотеза о наличии гомоскедастичности.
Если при оценивании более чем одной функции получается значимая оценка a1, то ориентиром при определении характера гетероскедастичности может служить лучшая из них.
Слайд 55Устранение гетероскедастичности
Часть 2
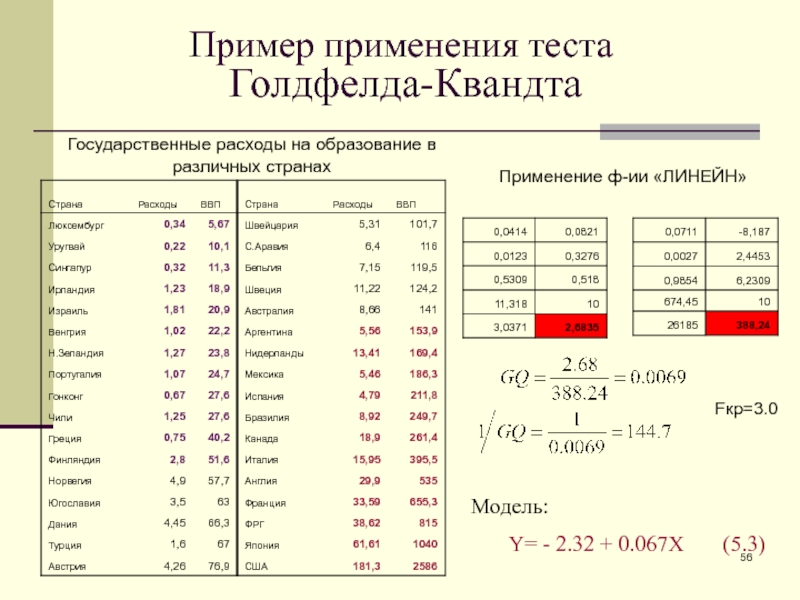
Слайд 56Пример применения теста
Голдфелда-Квандта
Государственные расходы на образование в различных странах
Fкр=3.0
Применение
ф-ии «ЛИНЕЙН»
Модель:
Y= - 2.32 + 0.067X
(5.3)
Слайд 57Наличие гетероскедастичности
При наличии гетероскедастичности последствия применения МНК будут следующими:
- оценки параметров могут остаться по-прежнему несмещенными и линейными;
- оценки не будут эффективными, т.е. не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра. Они не будут даже асимптотически эффективными. А увеличение дисперсии оценок снижает вероятность получения максимально точных оценок;
- дисперсии оценок параметров будут рассчитываться со смещением;
- выводы, получаемые на основе соответствующих t- и F— статистик, а также интервальные оценки будут ненадежными. Вполне вероятно, что стандартные ошибки параметров будут занижены, a t - статистики завышены, что может привести к признанию статистически значимыми параметры, которые таковыми на самом деле не являются.
Слайд 58Наличие гетероскедастичности
При установлении гетероскедастичности возникает необходимость преобразования модели
с целью устранения данного недостатка.
Вид преобразования зависит от
того, известны или нет дисперсии отклонении σi2.
В случае, если дисперсии отклонений известны для каждого наблюдения, применяется взвешенный метод наименьших квадратов (ВМНК).
Гетероскедастичность устраняется, если разделить каждое наблюдаемое значение на соответствующее ему значение дисперсии.
Слайд 59Метод исправления гетероскедастичности
Имеем:
1. Спецификацию модели: Yt=a0+a1x1t+a2x2t+a3x3t+ut (5.4)
2. Выборку наблюдений за переменными
{Y,x1,x2,x3}
3. Модель по этим данным гетероскедастична.
4. Известны значения σ(ut) в
каждом наблюдении.
Задача: преобразовать модель так, чтобы случайные возмущения были гомоскедастичны.
Слайд 60Метод исправления гетероскедастичности
Способ 1. Делится каждое уравнение наблюдений на свое
σ(ut) и получается:
Тогда дисперсия случайного возмущения в каждом уравнении наблюдений
есть:
Модель (5.2) в каждом уравнении наблюдения имеет одинаковые дисперсии случайного возмущения равные 1.
Недостаток способа – оценить σ(ut) не возможно!
(5.5)
Слайд 61Метод исправления гетероскедастичности
Способ 2.
Предполагаем, что σ(ut)=λxkt, где xkt регрессор «вызывающий»
гетероскедастичность. Пусть для примера это регрессор x2t.
Уравнение (5.4) делится на
значение этого регрессора.
Дисперсия случайного возмущения при этом есть:
Уравнения модели имеют постоянную дисперсию случайного возмущения равную λ2.
Слайд 62Метод исправления гетероскедастичности
Рассмотренные способы устранения гетероскедастичности носят название «Взвешенный метод
наименьших квадратов».
Теорема. Если в схеме Гаусса-Маркова не выполняется предпосылка о
гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является:
где: Р матрица ковариаций случайных возмущений в уравнения наблюдений:
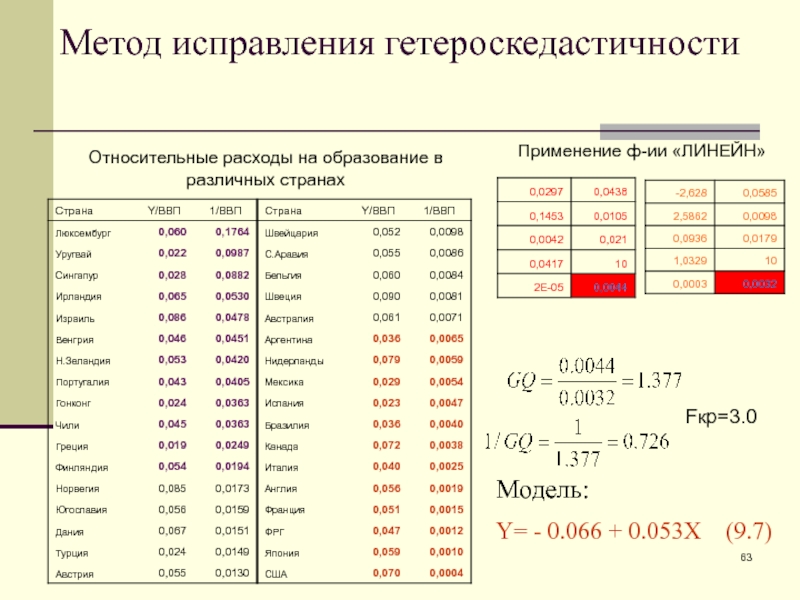
Слайд 63Метод исправления гетероскедастичности
Применение ф-ии «ЛИНЕЙН»
Относительные расходы на образование в различных
странах
Fкр=3.0
Модель:
Y= - 0.066 + 0.053X (9.7)
Слайд 64Модель:
Y = - 0.066 + 0.053X Гомоскедастичность
Модель (исходная):
Y = - 2.32 + 0.067X
Гетероскедастичность
Слайд 65Метод исправления гетероскедастичности
(5.7)
(5.3)
Диаграмма рассеяния и графики моделей с гетероскедастичными и
гомоскедастичными случайными возмущениями.
Слайд 66Метод исправления гетероскедастичности - 2
Для применения ВМНК необходимо
знать фактические значения дисперсий отклонений σi2. На практике такие значения
известны крайне редко. Поэтому, чтобы применить ВМНК, необходимо сделать реалистические предположения о значениях σi2. Чаще всего предполагается, что дисперсии отклонений пропорциональны или значениям хi или значениям хi2.
Если предположить, что дисперсии σi2 пропорциональны значениям фактора хi2, то тогда уравнение (5.7) преобразуется делением его левой и правой частей на хi , получим :
(5.10)
Здесь для отклонений выполняется условие гомоскедастичности.
Применяя обычный МНК к регрессии (5.10) в преобразованных переменных получим оценки параметров, после чего возвращаемся к исходному уравнению (5.7). Отметим, что в регрессии (5.7) по сравнению с исходным уравнением параметры поменялись ролями: свободный член а0 стал параметром при переменной, а параметр a1 - свободным членом
Слайд 67Метод исправления гетероскедастичности - 3
уi = a0 + a1∙xi +
εi (5.7)
Если
предположить, что дисперсии σi2 пропорциональны значениям фактора хi, то тогда уравнение (5.7) преобразуется делением его левой и правой частей на √хi , получим :
(5.11)
Для отклонений выполняется условие гомоскедастичности.
Применяя обычный МНК к регрессии (5.11) в преобразованных переменных получим оценки параметров, после чего возвращаемся к исходному уравнению (5.7).
Слайд 68Метод исправления гетероскедастичности - 4
Если в уравнении регрессии
присутствует несколько объясняющих переменных, вместо конкретной переменной xj используется исходное
уравнение множественной регрессии
y = a0 + a1∙x1 + a2∙x2 + a3∙x3 … + an∙xn + εi (5.12)
т.е. фактически линейная комбинация факторов. В этом случае получают следующую регрессию:
(5.13)
Для отклонений выполняется условие гомоскедастичности.
Применяя обычный МНК к регрессии (5.13) в преобразованных переменных получим оценки параметров, после чего возвращаемся к исходному уравнению (5.12).
Слайд 69Метод исправления гетероскедастичности - 5
2. Воспользуемся предположением тестов Голдфельда —
Квандта и Спирмена о том, что ошибки случайных возмущений связаны
с абсолютными значениями регрессоров. Предположим, что стандартную ошибку случайных возмущений, можно представить в виде
где μ — показатель степени, с помощью которого учитывается возможность нелинейной связи между ошибкой остатка и абсолютным весом регрессоров
Слайд 70Метод исправления гетероскедастичности
Заменив в первом уравнении на ….. Получаем следующее
уравнение
(5.12)
Количественные характеристики случайной переменной
Введя новые переменные
и сделав соответствующую замену,
вновь получим модель в виде линейного алгебраического уравнения с гомоскедастичными остатками.
Слайд 71Метод исправления гетероскедастичности
Остается открытым вопрос о значении μ. Начинают процесс
устранения гетероскедастичности со значения μ = 1. Если при μ
= 1 модель (5.12) остается гетероскедастичной, то вводится приращение Δμ (например, Δμ = 0,5) и модель (5.12) проверяется на гетероскедастичность при μ = μ + Δμ. Меняя знак и абсолютное значение приращения Δμ, добиваются выполнения соотношений GQ≤Fкрит и GQ-1≤Fкрит.
Функцию называют весовой функцией.
Заметим, что в спецификации модели вида (5.12) значения pt во всех наблюдениях будут равны. Говорят, что преобразование
выравнивает веса регрессоров во всех наблюдениях.
Слайд 72ВЗВЕШАННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Слайд 73Формулировка взвешенного метода наименьших квадратов (ВМНК)
Формулировка ВМНК – это формализация
рассмотренного алгоритма.
Для того, чтобы его сформулировать достаточно обобщить те процедуры,
которые предпринимались для оценки параметров линейной модели в условиях гетероскедастичности:
1. Подбирается функция pt, с помощью которой моделируется зависимость дисперсии случайных возмущений от суммарного веса регрессоров в уравнениях наблюдений;
2. Все переменные в каждом наблюдении умножаются на ;
3. К преобразованной таким образом выборке применяется метод наименьших квадратов (МНК) для получения оценок параметров модели.
Слайд 74Взвешенный МНК
Введем матрицу W размерностью (n x k):
(5.13)
Тогда преобразование
переменных можно представить в виде произведений:
(
) и (WX), и процедура метода наименьших квадратов примет вид:
(5.14)
Процедура (5.14) обеспечила получение состоятельных оценок параметров линейной модели при выполнении всех предпосылок теоремы Гаусса — Маркова, кроме второй предпосылки о гомоскедастичности случайных возмущений.
Слайд 75Взвешенный МНК
Этот факт нашел свое отражение в теореме.
Но прежде,
чем ее сформулировать, введем матрицу ковариаций вектора случайных возмущений в
виде
(5.15)
Теорема.
Если в схеме Гаусса — Маркова ковариационная матрица вектора случайных возмущений имеет вид (5.15), то оптимальной процедурой, доставляющей состоятельные оценки параметров линейной модели, является
(5.16)
Процедура (5.16) называется взвешенным методом наименьших квадратов