Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1_09.ppt
Содержание
- 1. 1_09.ppt
- 2. Модель ХаббардаМодель была предложена в 1964 г.
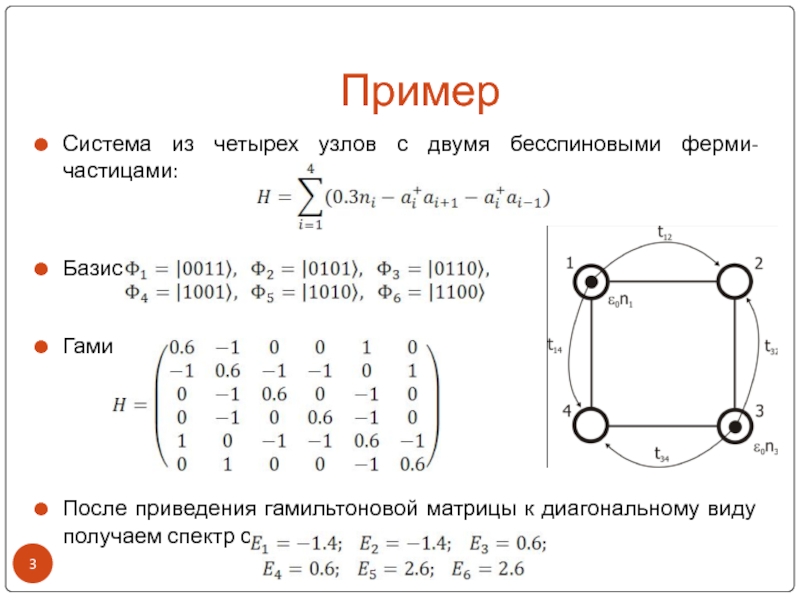
- 3. ПримерСистема из четырех узлов с двумя бесспиновыми
- 4. Модель Хаббарда. Приближение среднего поляДля модели Хаббарда
- 5. ПримерСистема из трех узлов и двух частиц с противоположными спинами:Базис системы:Гамильтонова матрица:
- 6. ПримерСпектр без взаимодействия:Разрешенные одночастичные уровни для одной проекции спина:Основное состояние:Основное состояние невырождено
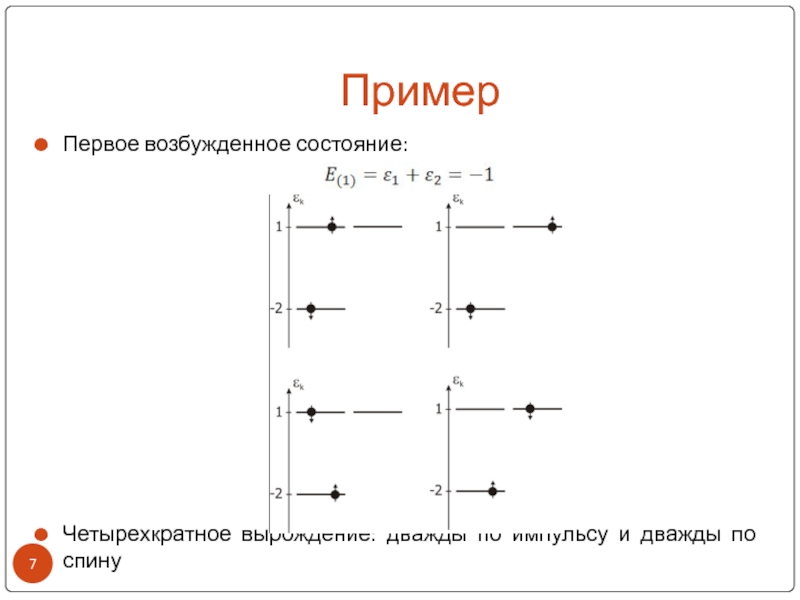
- 7. ПримерПервое возбужденное состояние:Четырехкратное вырождение: дважды по импульсу и дважды по спину
- 8. ПримерВторое возбужденное состояние также четырехкратно вырожденоСпектр системы:При
- 9. Инварианты в модели ХаббардаВ модели Хаббарда сохраняется
- 10. Расчет среднихСреднее число частиц на узле в основном состоянии:Недиагональные корреляторы:Вырожденные состояния:
- 11. Скачать презентанцию
Модель ХаббардаМодель была предложена в 1964 г. для объяснения фазовых переходов "металл – изолятор" в переходных металлах c узкими зонамиМодель Хаббарда (и ее расширенные аналоги) в настоящее время стала популярной в
Слайды и текст этой презентации
Слайд 1Модель Хаббарда.
Приближение среднего поля.
Инварианты в модели Хаббарда.
Расчет средних
1.9. Ферми-системы.
Модель
Хаббарда
Слайд 2Модель Хаббарда
Модель была предложена в 1964 г. для объяснения фазовых
переходов "металл – изолятор" в переходных металлах c узкими зонами
Модель
Хаббарда (и ее расширенные аналоги) в настоящее время стала популярной в связи с исследованием высокотемпературных сверхпроводников, наноструктур, квантовых точек и ямГамильтониан для ферми-газа с кулоновским взаимодействием:
В координатном представлении:
Слайд 3Пример
Система из четырех узлов с двумя бесспиновыми ферми-частицами:
Базис этой системы:
Гамильтонова
матрица:
После приведения гамильтоновой матрицы к диагональному виду получаем спектр системы:
Слайд 4Модель Хаббарда.
Приближение среднего поля
Для модели Хаббарда и ее модификаций нельзя
строго провести аналитический расчет
Приближение среднего поля: задача из многочастичной превращается
в эффективную одночастичную:В импульсном представлении гамильтониан диагонален:
Для расчета средних чисел заполнения необходимо решить самосогласованную систему уравнений (модель Стонера)
Слайд 5Пример
Система из трех узлов и двух частиц с противоположными спинами:
Базис
системы:
Гамильтонова матрица:
Слайд 6Пример
Спектр без взаимодействия:
Разрешенные одночастичные уровни для одной проекции спина:
Основное состояние:
Основное
состояние невырождено
Слайд 7Пример
Первое возбужденное состояние:
Четырехкратное вырождение: дважды по импульсу и дважды по
спину
Слайд 8Пример
Второе возбужденное состояние также четырехкратно вырождено
Спектр системы:
При ненулевом взаимодействии:
Приближение среднего
поля изменило бы спектр на величину порядка
Для возбужденных уровней приближение
среднего поля работает хужеЕсли при слабом взаимодействии еще удается качественно проследить за изменением спектра, то при U~t это становится невозможным
Слайд 9Инварианты в модели Хаббарда
В модели Хаббарда сохраняется число частиц:
Для частиц
со спином гамильтониан коммутирует с оператором полной проекции спина на
ось z:Гамильтонова матрица может быть представлена в блочно-диагональном виде:
Слайд 10Расчет средних
Среднее число частиц на узле в основном состоянии:
Недиагональные корреляторы:
Вырожденные
состояния:
