Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1_16.ppt
Содержание
- 1. 1_16.ppt
- 2. Отклик системы на внешнее полеПри численном анализе
- 3. Отклик системы на внешнее полеВекторный потенциал:Соотношение Кубо:
- 4. Отклик системы на внешнее полеФурье-компоненты векторного потенциала и тока:С учетом соотношения Кубо:
- 5. Отклик системы на внешнее полеУчитывая связь векторного
- 6. Плотность состоянийПлотность состояний – важная физическая величина,
- 7. Плотность состоянийСпектральная плотность системы при нулевой температуре:В узельном представлении:
- 8. Плотность состоянийЩель в спектре возбуждений:Если Δ
- 9. Плотность состоянийЕсли для известного вектора ? требуется
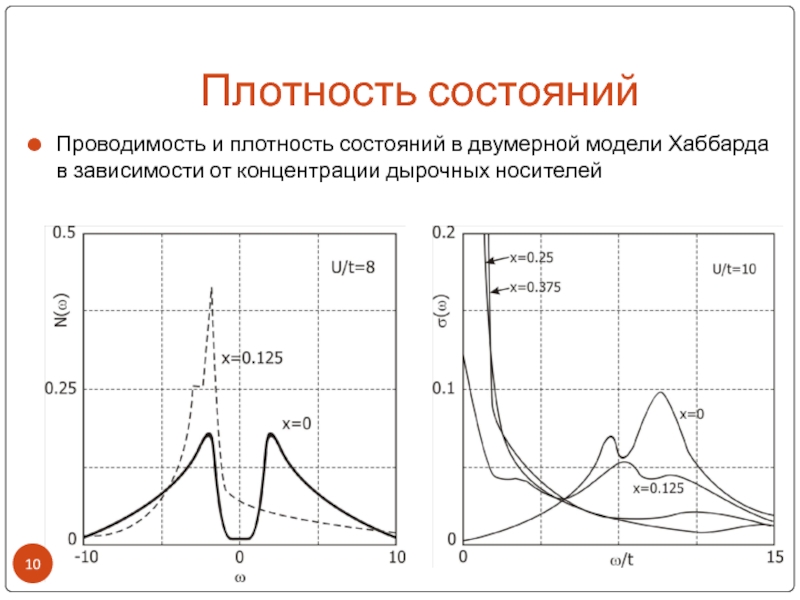
- 10. Плотность состоянийПроводимость и плотность состояний в двумерной модели Хаббарда в зависимости от концентрации дырочных носителей
- 11. Скачать презентанцию
Отклик системы на внешнее полеПри численном анализе квантовых систем конечной целью расчета часто являются такие физические величины, как плотность состояний, проводимость, восприимчивость и т.д. Это достаточно сложные корреляторы, для расчета которых,
Слайды и текст этой презентации
Слайд 1Отклик системы на внешнее поле. Плотность состояний
1.16. Расчет функций линейного
отклика и плотности состояний
Слайд 2Отклик системы на внешнее поле
При численном анализе квантовых систем конечной
целью расчета часто являются такие физические величины, как плотность состояний,
проводимость, восприимчивость и т.д. Это достаточно сложные корреляторы, для расчета которых, как правило, требуется комбинировать результаты расчетов с различным числом частиц в системеОператор тока в представлении чисел заполнения для системы решеточных фермионов или бозонов:
Парамагнитная часть плотности тока и плотность кинетической энергии движения тока:
Слайд 3Отклик системы на внешнее поле
Векторный потенциал:
Соотношение Кубо: если на систему
действует внешнее возмущение
то имеет место линейное соотношение между фурье-компонентами среднего
значения и силы:Обобщенная восприимчивость:
Потенциал возмущения за счет внешнего поля:
Слайд 4Отклик системы на внешнее поле
Фурье-компоненты векторного потенциала и тока:
С учетом
соотношения Кубо:
Слайд 5Отклик системы на внешнее поле
Учитывая связь векторного потенциала и напряженности
электрического поля в длинноволновом пределе получаем выражение для проводимости:
При низких
температурах главный вклад будет давать основное состояние, а также матричные элементы между основным состоянием и ближайшими возбужденными. Величина ??? преобразуется в сумму дельта-функций, и наиболее сложная задача состоит в корректном расчете следующего спектрального коррелятора:Это выражение можно вычислять непосредственно в процессе применения алгоритма Ланцоша, который с высокой точностью определяет несколько возбужденных состояний над основным.
Слайд 6Плотность состояний
Плотность состояний – важная физическая величина, необходимая при расчете
различных квантово-механических средних, ей удобно пользоваться, когда подынтегральное выражение зависит
только от энергии частиц, например:для модели сильной связи
для свободного газа
Плотность состояний для системы фермионов со спинами:
Одночастичная плотность состояний может быть представлена в виде:
Слайд 7Плотность состояний
Спектральная плотность системы при нулевой температуре:
В узельном представлении:
Слайд 8Плотность состояний
Щель в спектре возбуждений:
Если Δ
нет, и плотность состояний непрерывна как функция энергии
Для расчета необходимо
вычислить сложный корреляторМатричные элементы в корреляторе рассчитываются между состояниями с различным числом частиц. Тем не менее, для его расчета может быть применен алгоритм Ланцоша
В процессе работы алгоритма Ланцоша при увеличении числа итераций возникают паразитические псевдособственные векторы, которые либо дублируют уже существующие собственные векторы, либо имеют очень плохую невязку. Однако для расчета подобных корреляторов можно игнорировать проблему возникновения паразитических векторов
Слайд 9Плотность состояний
Если для известного вектора ? требуется вычислить вектор ?=?(?)?,
где явный вид оператора ? известен только в базисе собственных
векторов матрицы ?, то решить эту задачу можно с помощью простого алгоритма ЛанцошаВ нашем случае ? – многочастичная волновая функция основного состояния системы; ? – гамильтониан системы
Плотность состояний:
В качестве первого вектора, по которому образуется подпространство Крылова, берется вектор ?, по завершении итерационной процедуры алгоритм Ланцоша дает все необходимые скалярные произведения (?,??)