Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
2_13.ppt
Содержание
- 1. 2_13.ppt
- 2. t-J-модельt-J-модель:Разобьем гамильтониан на две части, описывающие четные и нечетные связи:Разложение статистической суммы:
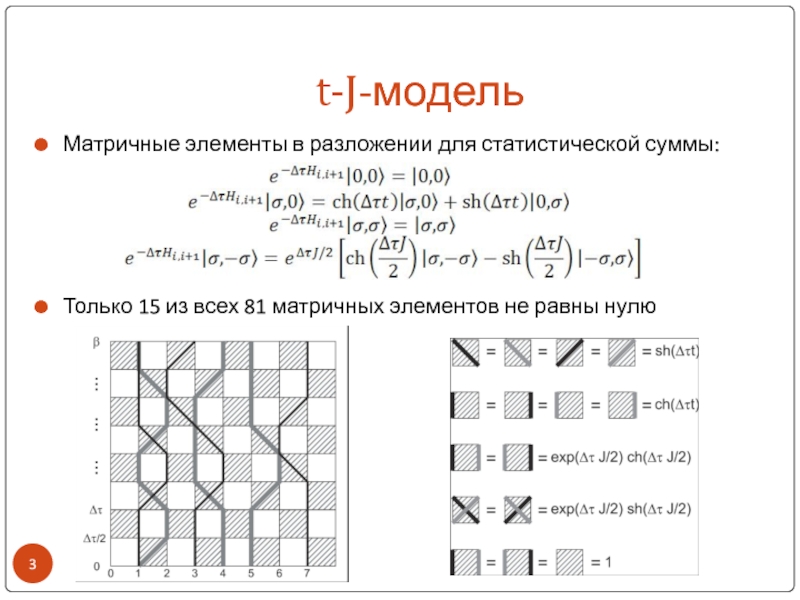
- 3. t-J-модельМатричные элементы в разложении для статистической суммы:Только 15 из всех 81 матричных элементов не равны нулю
- 4. t-J-модельЛокальные изменения фазовых траекторий. Последняя процедура необходима для обеспечения эргодичности алгоритма
- 5. t-J-модельРасчет термодинамических средних (энергии, диагональных и недиагональных
- 6. Моделирование сверхпроводящих плоскостей в ВТСПДвумерная многозонная модель
- 7. Моделирование сверхпроводящих плоскостей в ВТСПРазбиение плоскости CuO2
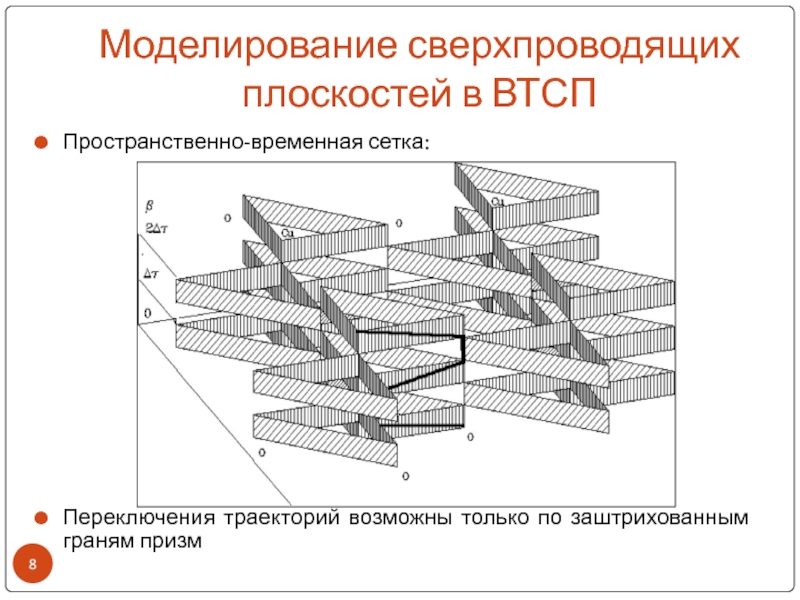
- 8. Моделирование сверхпроводящих плоскостей в ВТСППространственно-временная сетка:Переключения траекторий возможны только по заштрихованным граням призм
- 9. Моделирование сверхпроводящих плоскостей в ВТСПЭволюция мировых линий
- 10. Моделирование сверхпроводящих плоскостей в ВТСПРазбиение плоскости CuO2 на пятиузельные ячейки:
- 11. Скачать презентанцию
t-J-модельt-J-модель:Разобьем гамильтониан на две части, описывающие четные и нечетные связи:Разложение статистической суммы:
Слайды и текст этой презентации
Слайд 1t-J-модель.
Моделирование сверхпроводящих плоскостей в ВТСП
2.13. Траекторный алгоритм Монте-Карло для конкретных
задач
Слайд 2t-J-модель
t-J-модель:
Разобьем гамильтониан на две части, описывающие четные и нечетные связи:
Разложение
статистической суммы:
Слайд 3t-J-модель
Матричные элементы в разложении для статистической суммы:
Только 15 из всех
81 матричных элементов не равны нулю
Слайд 4t-J-модель
Локальные изменения фазовых траекторий. Последняя процедура необходима для обеспечения эргодичности
алгоритма
Слайд 5t-J-модель
Расчет термодинамических средних (энергии, диагональных и недиагональных корреляционных функций):
Наличие проблемы
знака зависит от вида граничных условий в системе. При фиксированных
(нулевых) граничных условиях статистические веса всегда положительны
Слайд 6Моделирование сверхпроводящих плоскостей в ВТСП
Двумерная многозонная модель Эмери в дырочном
представлении:
Модель Эмери была предложена для описания движения дырок в плоскости
CuO2 с учетом особенностей электронной структуры ВТСП, а также с учетом различия атомных уровней на медных и кислородных узлах, кулоновского взаимодействия на узлах меди, узлах кислорода и между нимиДаже в таком упрощенном виде (без учета перескоков на следующие за ближайшими узлы, прямых перескоков «кислород – кислород» и т.д.) гамильтониан оказывается чрезвычайно сложным для теоретического анализа
Гамильтониан коммутирует с операторами полного числа частиц и проекции полного спина на произвольно выбранную ось
Слайд 7Моделирование сверхпроводящих плоскостей в ВТСП
Разбиение плоскости CuO2 на трехузельные ячейки:
Для
достижения погрешности результатов в несколько процентов обычно достаточно выполнения условия
Слайд 8Моделирование сверхпроводящих плоскостей в ВТСП
Пространственно-временная сетка:
Переключения траекторий возможны только по
заштрихованным граням призм
Слайд 9Моделирование сверхпроводящих плоскостей в ВТСП
Эволюция мировых линий от одного временного
среза к другому определяется матричными элементами оператора эволюции
Эти матричные элементы
могут быть рассчитаны только численно:Оператор, диагональный в представлении чисел заполнения:
Для расчета оператора, недиагонального в представлении чисел заполнения (например, энергии), необходимо рассчитывать матричные элементы вида
Слайд 10Моделирование сверхпроводящих плоскостей в ВТСП
Разбиение плоскости CuO2 на пятиузельные ячейки:
