Цифровой логический уровень

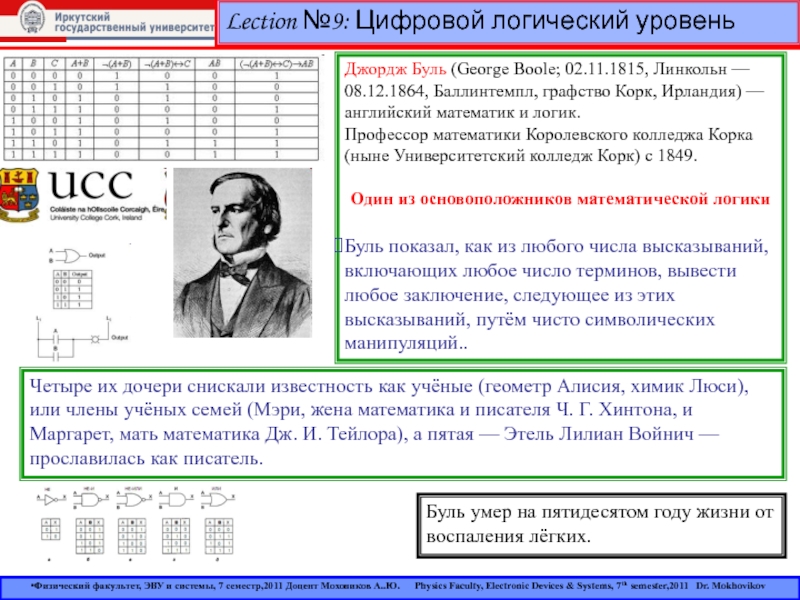
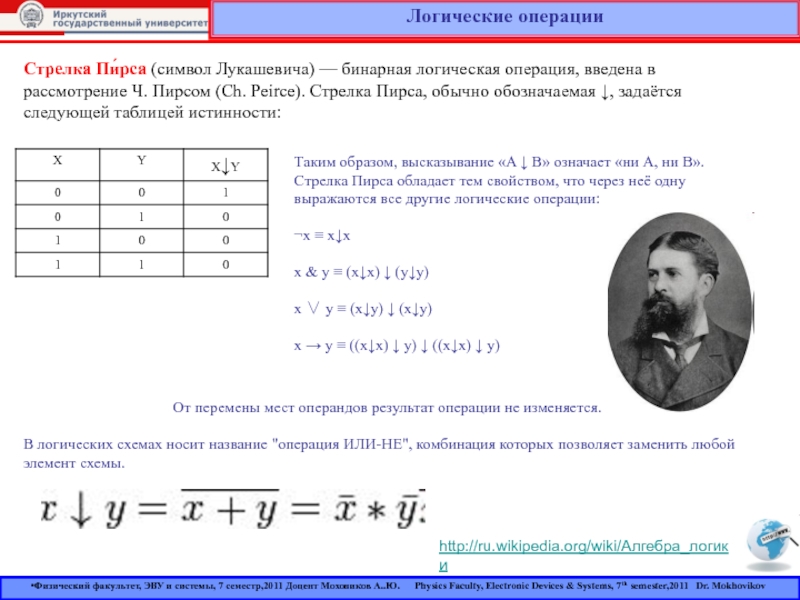
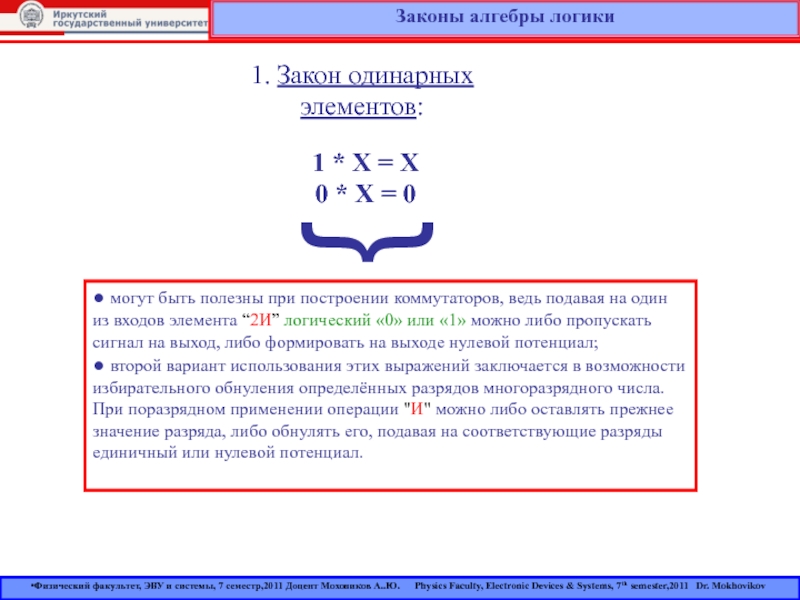
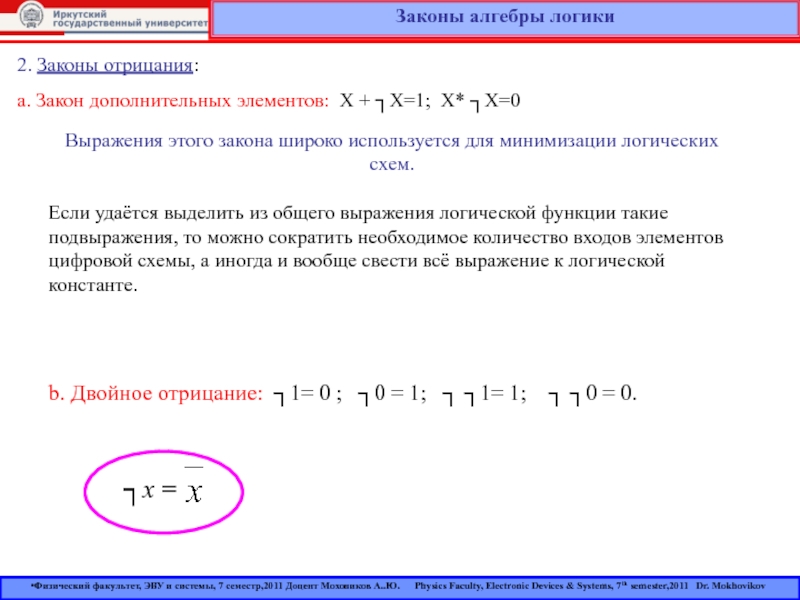
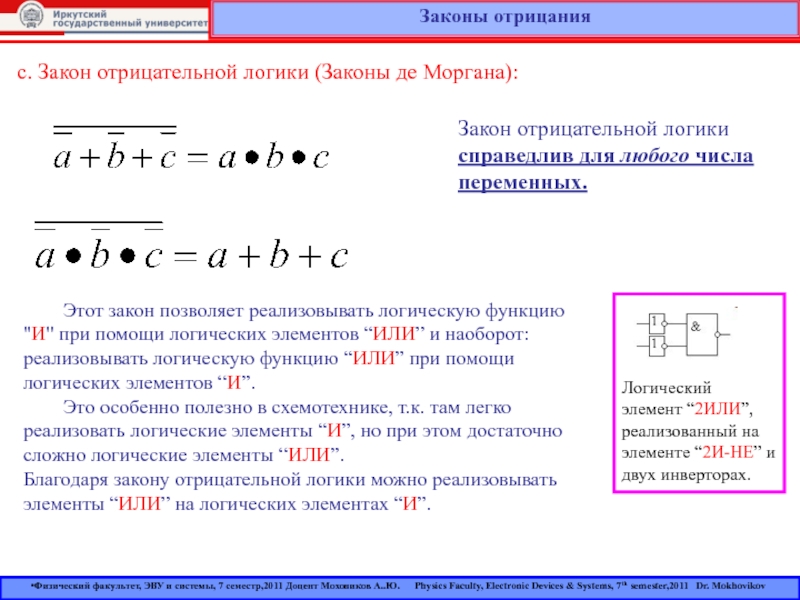
Корк, Ирландия) — английский математик и логик.
Профессор математики Королевского

колледжа Корка (ныне Университетский колледж Корк) с 1849.

Один из основоположников математической логики

Буль показал, как из любого числа высказываний, включающих любое число терминов, вывести любое заключение, следующее из этих высказываний, путём чисто символических манипуляций..

Четыре их дочери снискали известность как учёные (геометр Алисия, химик Люси), или члены учёных семей (Мэри, жена математика и писателя Ч. Г. Хинтона, и Маргарет, мать математика Дж. И. Тейлора), а пятая — Этель Лилиан Войнич — прославилась как писатель.

Буль умер на пятидесятом году жизни от воспаления лёгких.

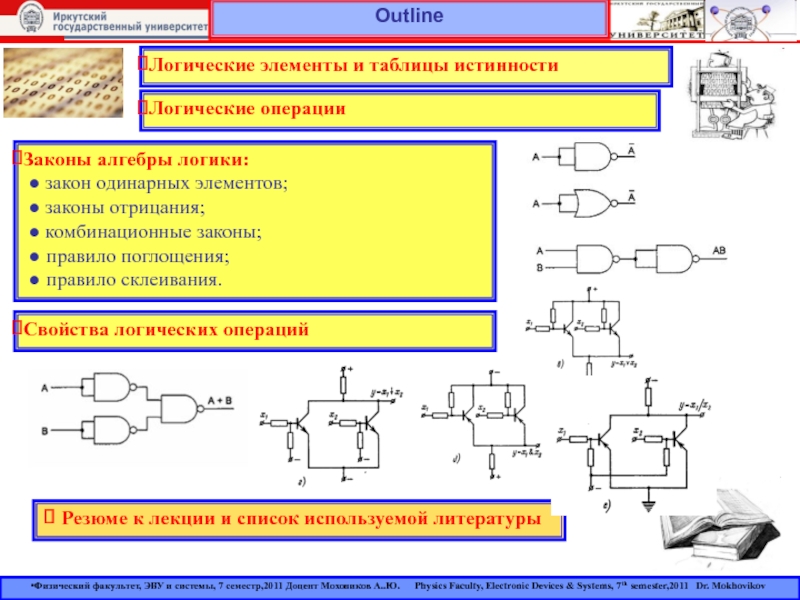
Lection №9: Цифровой логический уровень

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

одинарных элементов;
● законы отрицания;
● комбинационные законы;
●

правило поглощения;
● правило склеивания.

Свойства логических операций

Резюме к лекции и список используемой литературы

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

одних и тех же логических элементов – «кирпичиков» любого цифрового

узла

!

Логический элемент – это такая схема, у которой несколько входов и один выход.
Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.

Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

Обычно сигнал от 0 до 1 В представляет одно значение (н-р, 0), а сигнал от 2 до 5 В — другое значение (н-р, 1).

Электронные устройства, которые называются вентилями, могут вычислять различные функции от этих двузначных сигналов.

Логические элементы и таблицы истинности

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

его не сложно: “1” на выходе элемента «И» возникает только

тогда, когда на оба входа поданы единицы.
Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.

Элемент «ИЛИ» (OR)

Иначе его называют «дизъюнктор».

На выходе возникает “1”, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица.

Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой " . " (может также обозначаться знаками /\ или &).

Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом).

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

выражаемая словом "не", называется инверсией или отрицанием и обозначается чертой

над высказыванием.  

Элемент «И-НЕ» (NAND)







Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» - единица. И наоборот.

Элемент «ИЛИ-НЕ» (NOR)

Элемент «Исключающее ИЛИ» (XOR)

Операция, которую он выполняет, часто называют «сложение по модулю 2».
На самом деле, на этих элементах строятся цифровые сумматоры.

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

"из ... следует",  "... влечет ...",  называется импликацией (лат. implico

— тесно связаны) и обозначается знаком → . Высказывание   А → В ложно тогда и только тогда, когда  А  истинно,  а  В  ложно.

РАВНОСИЛЬНО  
Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "... равносильно ...", называется эквиваленцией или двойной импликацией и обозначается знаком   ↔ или  ~ .
  Высказывание А ↔ В истинно тогда и только тогда, когда значения А и В совпадают.      

Также как в обычной математике в алгебре логики имеется старшинство операций.
При этом первым выполняется:
Действие в скобках
Операция с одним операндом (одноместная операция) – НЕ
Конъюнкция - И
Дизъюнкция - ИЛИ
Сумма по модулю два.

АКСИОМЫ алгебры логики описывают действие логических функций "И" и "ИЛИ" и записываются следующими выражениями:
0 * 0 = 0; 0 * 1 = 0; 1 * 0 = 0; 1 * 1 = 1;
0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 1;

http://digital.sibsutis.ru/digital/AlgLog.htm

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

а Истина — с логической единицей, а операции отрицания (НЕ),

конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании.   

http://ru.wikipedia.org/wiki/Алгебра_логики

Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными.
(это логический элемент «и-не»)

Как и любую булеву операцию, штрих Шеффера можно выразить через отрицание и дизъюнкцию:

Отрицание

Дизъюнкция

Конъюнкция

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

введена в рассмотрение Ч. Пирсом (Сh. Peirce). Стрелка Пирса, обычно

обозначаемая ↓, задаётся следующей таблицей истинности:

Таким образом, высказывание «A ↓ B» означает «ни A, ни B». Стрелка Пирса обладает тем свойством, что через неё одну выражаются все другие логические операции:

¬x ≡ x↓x

x & y ≡ (x↓x) ↓ (y↓y)

x ∨ y ≡ (x↓y) ↓ (x↓y)

x → y ≡ ((x↓x) ↓ y) ↓ ((x↓x) ↓ y)

От перемены мест операндов результат операции не изменяется.

В логических схемах носит название "операция ИЛИ-НЕ", комбинация которых позволяет заменить любой элемент схемы.

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

= X
0 * X = 0
}
● могут быть полезны

при построении коммутаторов, ведь подавая на один из входов элемента “2И” логический «0» или «1» можно либо пропускать сигнал на выход, либо формировать на выходе нулевой потенциал;
● второй вариант использования этих выражений заключается в возможности избирательного обнуления определённых разрядов многоразрядного числа.
При поразрядном применении операции "И" можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды единичный или нулевой потенциал.

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

* X = 0
}
Например, требуется обнулить 6, 3 и 1

разряды.
Тогда:

Видно, что для обнуления необходимых разрядов
в маске (нижнее число) на месте соответствующих разрядов записаны нули, в остальных разрядах записаны единицы.

В исходном числе (верхнее число) на месте 6 и 1 разрядов
находятся единицы.
После выполнения операции "И" на этих местах появляются
нули.
На месте третьего разряда в исходном числе находится «0».
В результирующем числе на этом месте тоже присутствует «0».
Остальные разряды, как и требовалось по условию задачи, не изменены.

= * = & =

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

= X
● Точно так же можно записывать единицы в нужные

нам разряды. В этом случае необходимо воспользоваться нижними двумя выражениями закона одинарных элементов.
При поразрядном применении операции “ИЛИ” можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды нулевой или единичный потенциал.

Пусть требуется записать единицы в 7 и 6 биты числа. Тогда:

}

Здесь в маску (нижнее число) мы записали единицы в
седьмой и шестой биты.
Остальные биты содержат нули, и, =>, не могут изменить первоначальное состояние исходного числа, что мы и видим в результирующем числе под чертой.

Это позволяют использовать логические элементы с большим
количеством входов в качестве элементов с меньшим количеством входов.
Для этого неиспользуемые входы в схеме “И” должны быть подключены к источнику питания

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

┐X=1; X* ┐X=0
Выражения этого закона широко используется для минимизации логических

схем.

Если удаётся выделить из общего выражения логической функции такие подвыражения, то можно сократить необходимое количество входов элементов цифровой схемы, а иногда и вообще свести всё выражение к логической константе.

b. Двойное отрицание: ┐1= 0 ; ┐0 = 1; ┐ ┐1= 1; ┐ ┐0 = 0.

┐x =

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

логики справедлив для любого числа переменных.
Этот закон позволяет реализовывать логическую

функцию "И" при помощи логических элементов “ИЛИ” и наоборот: реализовывать логическую функцию “ИЛИ” при помощи логических элементов “И”.
Это особенно полезно в схемотехнике, т.к. там легко реализовать логические элементы “И”, но при этом достаточно сложно логические элементы “ИЛИ”.
Благодаря закону отрицательной логики можно реализовывать элементы “ИЛИ” на логических элементах “И”.

Логический элемент “2ИЛИ”, реализованный на элементе “2И-НЕ” и двух инверторах.

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

соответствуют комбинационным законам обычной алгебры, но есть и отличия.
a. Закон

тавтологии (многократное повторение): X+X+X+X=X; X*X*X*X=X

Этот закон позволяет использовать логические элементы с большим количеством входов в качестве элементов с меньшим количеством входов.

Например, можно реализовать двухвходовую схему 2И на элементе 3И:

или использовать схему 2И-НЕ в качестве обычного инвертора:

Однако следует предупредить, что объединение нескольких входов увеличивает входные токи логического элемента и его ёмкость, что увеличивает ток потребления предыдущих элементов и отрицательно сказывается на быстродействии цифровой схемы в целом.

http://digital.sibsutis.ru/digital/AlgLog.htm

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

X1(X2+X3)= X1X2 + X1X3

http://digital.sibsutis.ru/digital/AlgLog.htm
X1+X2X3=(X1+X2)(X1+X3)=/ докажем это путём раскрытия скобок/=

X1X1+ X1X3+ X1X2+ X2X3= X1(1+X3+X2)+ X2X3= X1+X2X3

Доказательство:

Физический факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

X3 =X1(1+X2 X3)=X1
5. Правило склеивания
(выполняется только по одной переменной)
Физический

факультет, ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov

Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems,

7th semester,2011 Dr. Mokhovikov

А..Ю. Physics Faculty, Electronic Devices & Systems, 7th

semester,2011 Dr. Mokhovikov

авторы Михаил Гук, Виктор Юров
Книга «Архитектура ЭВМ», автор Танненбаум
Физический факультет,

ЭВУ и системы, 7 семестр,2011 Доцент Моховиков А..Ю. Physics Faculty, Electronic Devices & Systems, 7th semester,2011 Dr. Mokhovikov