Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реляционная алгебра
Содержание
- 1. Реляционная алгебра
- 2. СОДЕРЖАНИЕЯзыки запросов в БДСвойства бинарных операцийОперации реляционной алгебрыПримеры Эквивалентные преобразования и оптимизация выражений реляционной алгебры
- 3. Языки запросовКатегории языков:процедурные (как получить то, что
- 4. Замкнутость реляционной алгебры и свойства бинарных операцийАлгебра
- 5. Операции реляционной алгебрыОсновные операции:Теоретико-множественные (объединение, пересечение, разность)ПроекцияСелекция (выборка)Декартово произведение, соединениеДелениеДополнительные операцииПрисвоениеПереименованиеОбобщенная проекцияВнешнее соединение…
- 6. Теоретико-множественные операцииДва отношения R и S совместимы
- 7. Операция объединения Объединением совместимых отношений R и
- 8. Операция разности Разностью совместимых отношений R и
- 9. Операция пересеченияПересечением совместимых отношений R и S
- 10. Операция проекцииПроекцией отношения R со схемой R(A),
- 11. θ-сравнимость атрибутов и кортежей Пусть θ -
- 12. Операция селекции (ограничения)Пусть М и N –
- 13. Операция декартового произведенияДекартовым произведением отношений R и
- 14. Операция соединения Пусть М и N –
- 15. Эквисоединение и естественное соединениеЭквисоединение – это соединение
- 16. ПолусоединениеR[М θ N)S = {(t1) ⏐ t1
- 17. Образ кортежаОбразом реляционного отношения R(M,N) относительно кортежа
- 18. Операция деления (1)Делением отношения R(M,N) на отношение
- 19. Операция деления (2)Пример:R
- 20. FAC (FNo, Name, Dean, Bld, Fund)DEP (DNo,
- 21. Примеры запросов в РА (1)Проекция: Вывести список
- 22. Примеры запросов в РА (2)Композиция соединения, селекции
- 23. Примеры запросов в РА (3)Name=‘CSF’ – условие
- 24. Примеры операции деления1) Вывести номера преподавателей, преподающих во
- 25. Дополнительные операции Дополнительные операцииПрисваиваниеПереименованиеОбобщенная проекцияВнешнее соединение…
- 26. Операция присваиваниеОперация присваивания (←) предоставляет удобный способ
- 27. Операция переименованияПозволяет именовать отношения вместе с их
- 28. Операция обобщенной проекцииОбобщенная проекция расширяет операцию проекции,
- 29. Внешнее соединениеВнешнее соединение является расширением обычного соединения,
- 30. Внешнее соединение - ПримерыFAC FNo
- 31. Внешнее соединение слеваFAC FNo Name
- 32. Внешнее соединение справаFAC FNo Name
- 33. Полное внешнее соединение4) Полное внешнее соединение
- 34. Эквивалентные преобразования выражений1) Коммутативность селекций: σF(σG(R))=σG(σF(R))=σF&G(R)2) Коммутативность
- 35. Оптимизация выражений РАR(A,B) S(C,D)
- 36. Общие правила оптимизации РАОбщие правила оптимизации выражений
- 37. Реляционная алгебра: выводыРеляционная алгебра:Формальный язык манипулирования данными
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 6. Реляционная алгебра
Национальный авиационный университет
Факультет компьютерных наук
Кафедра инженерии программного
обеспечения
Слайд 2СОДЕРЖАНИЕ
Языки запросов в БД
Свойства бинарных операций
Операции реляционной алгебры
Примеры
Эквивалентные преобразования
и оптимизация выражений реляционной алгебры
Слайд 3Языки запросов
Категории языков:
процедурные (как получить то, что надо)
непроцедурные (что надо
получить)
Формальные языки:
реляционная алгебра
реляционное исчисление (кортежное, доменное)
Язык запросов – это язык,
с помощью которого выбирается информация из базы данных.Формальные языки используются для создания языков запросов баз данных (Alpha, QUEL, QBE, SQL)
Слайд 4Замкнутость реляционной алгебры и свойства бинарных операций
Алгебра = данные (определенного
вида) + операции. Алгебра замкнутая, если операции дают данные того же
вида, что и данные в аргументе. Замкнутость позволяет вкладывать операции друг в друга.Реляционная алгебра = реляционные отношения + реляционные операции.
Реляционная алгебра замкнута.
Свойства бинарных операций:
Операция ϕ является коммутативной, если А ϕ В = B ϕ A
Операция ϕ является ассоциативной, если (А ϕ В) ϕ С = А ϕ (В ϕ С)
Операция ϕ является дистрибутивной по отношению к операции θ, если А ϕ (В θ С ) = (А ϕ В) θ (А ϕ С)
Слайд 5Операции реляционной алгебры
Основные операции:
Теоретико-множественные (объединение, пересечение, разность)
Проекция
Селекция (выборка)
Декартово произведение, соединение
Деление
Дополнительные
операции
Присвоение
Переименование
Обобщенная проекция
Внешнее соединение
…
Слайд 6Теоретико-множественные операции
Два отношения R и S совместимы (по объединению), если:
R
и S имеют одинаковую степень (арность), то есть одинаковое количество
атрибут.Домены соответствующих атрибутов должны быть совместимыми (1-й атрибут R определен на том же домене, что и 1-й атрибут S, и т.д.) .
Теоретико-множественные операции требуют совместимости их операндов
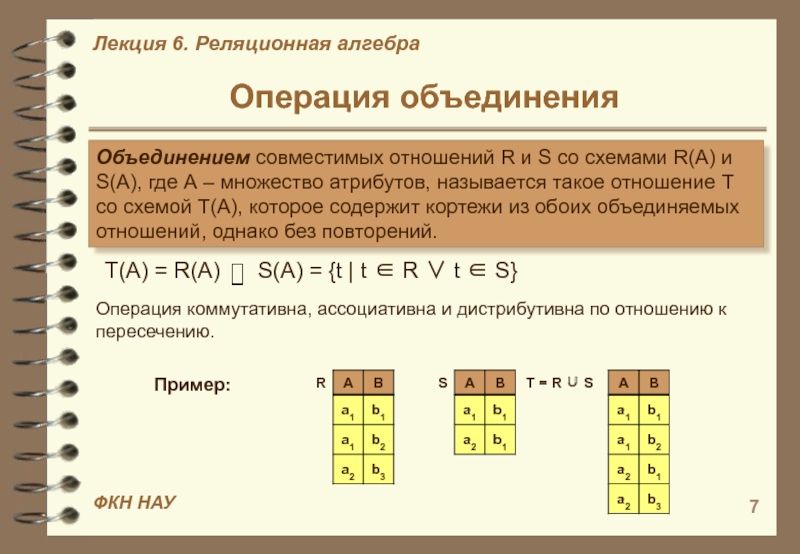
Слайд 7Операция объединения
Объединением совместимых отношений R и S со схемами
R(A) и S(A), где А – множество атрибутов, называется такое
отношение T со схемой Т(A), которое содержит кортежи из обоих объединяемых отношений, однако без повторений.Операция коммутативна, ассоциативна и дистрибутивна по отношению к пересечению.
Пример:
Слайд 8Операция разности
Разностью совместимых отношений R и S со схемами
R(A) и S(A), где А – множество атрибутов, называется такое
отношение T со схемой Т(A), которое содержит кортежи из отношения R, которых нет в отношении S.Операция не коммутативна, не ассоциативна и не дистрибутивна по отношению к другим операциям.
Т(А) = R(А) ⎯ S(А) = {t | t ∈ R & t ∉ S}
Пример:
Примечание: В РА на используется теоретико-множественная операция дополнения!!!
Слайд 9Операция пересечения
Пересечением совместимых отношений R и S со схемами R(A)
и S(A), где А – множество атрибутов, называется такое отношение
T со схемой Т(A), которое содержит кортежи, входящие в состав обоих отношений.Операция коммутативна, ассоциативна и дистрибутивна по отношению к объединению.
Т(А) = R(А) ∩ S(А) = {t | t ∈ R & t ∈ S}
Пример:
Пересечение выражается через разность: R ∩ S = R – (R – S)
Слайд 10Операция проекции
Проекцией отношения R со схемой R(A), где А –
множество атрибутов, по множеству атрибутов В, где В ⊂ А,
называется такое отношение S со схемой S(B), кортежи которого получаются из кортежей отношения R путем удаления значений, не принадле- жащих атрибутам, по которым производится проекция.S(B) = R[B] = {t[B] ⏐ t ∈ R}
Проекция обозначается так: R[B] или πВ(R)
Пример:
Примечание: Дубликаты строк удаляются
Слайд 11θ-сравнимость атрибутов и кортежей
Пусть θ - любой из следующих
операторов сравнения: =, ≠, < ≤, >, ≥. Атрибуты А
и В одного и того же или различных отношений называются θ-сравнимыми, если для любого значения а ∈ А и b ∈ B определено выражение а θ b.Наборы атрибутов М = (A1,…, Ak) и N = (B1,…,Bn) называются
θ-сравнимыми, если k = n и пары атрибутов (Ai, Bi) являются θ‑сравнимыи. В этом случае M θ N подразумевает следующее:
M θ N = (A1 θ B1) & … & (Ak θ Вk)
Если t – кортеж отношения, содержащего множества θ‑сравнимых атрибутов M и N, то запись запись t[M] θ t[N] подразумевает:
(t[A1] θ t[B1]) & … & (t[Ak] θ t[Вk]).
Слайд 12Операция селекции (ограничения)
Пусть М и N – наборы θ-сравнимых атрибутов
отношения R. Тогда селекцией отношения R по условию М θ N, обозначаемой
R[М θ N], называется такое отношение Т, которое имеет схему отношения R, и содержит те кортежи R, на которых истинно условие М θ N.Т(А) = R[M θ N] = {t | t ∈ R & t[M] θ t[N]}
Пример:
Операция также имеет следующую нотацию: σM θ N(R)
Один из наборов атрибутов M или N может быть константой.
Слайд 13Операция декартового произведения
Декартовым произведением отношений R и S со схемами
R(А) и S(B) (A и B – множества атрибутов), обозначаемым
R(A) x S(B), называется отношение Т со схемой Т(A,B), содержащее все возможные соединения кортежей отношений R и S:Операция коммутативна, ассоциативна и дистрибутивна по отношению к объединению и пересечению.
Т(А,В) = R(А) x S(B) = {(t1,t2) | t1 ∈ R & t2 ∈ S}
Пример:
Слайд 14Операция соединения
Пусть М и N – наборы θ-сравнимых атрибутов.
Соединением отношения R со схемой R(A,M) с отношением S со
схемой S(N,B) (A, B, M, N – множества атрибутов) по условию М θ N, обозначаемое R[М θ N]S, называется такое отношение Т со схемой T(А, M, N, B), кортежи которого получаются соедине- нием тех кортежей отношений R и S, на которых выполняется условие МθN.T = R[М θ N]S = {(t1, t2) ⏐ t1 ∈ R ∧ t2 ∈ S ∧ t1[М] θ t2[N]}
Пример:
Операция коммутативна и ассоциативна
Операция также обозначается: R M θ NS
Соединение выражается через произведение и селекцию: R M θ NS = σM θ N(R x S)
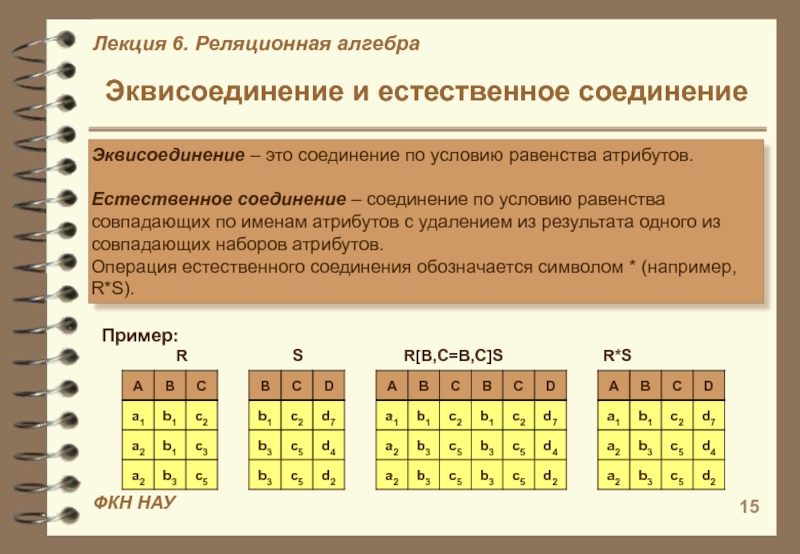
Слайд 15Эквисоединение и естественное соединение
Эквисоединение – это соединение по условию равенства
атрибутов.
Естественное соединение – соединение по условию равенства совпадающих по
именам атрибутов с удалением из результата одного из совпадающих наборов атрибутов. Операция естественного соединения обозначается символом * (например, R*S).
Пример:
R S R[B,C=B,C]S R*S
Слайд 16Полусоединение
R[М θ N)S = {(t1) ⏐ t1 ∈ R ∧
t2 ∈ S ∧ t1[М] θ t2[N]}
Пример:
R
S R[B,C=B,C)SR[М θ N)S = (R[М θ N]S)[A] – где А – набор атрибутов отношения R
Полусоединение выражается через соединение и проекцию:
Слайд 17Образ кортежа
Образом реляционного отношения R(M,N) относительно кортежа кортежа t1 ∈
R[M], изображаемым как It1(R), называется такое множество кортежей t2 ∈
R[N], для которых соединение кортежей (t1,t2) принадлежит отношению R.It1 ∈ R[M](R) = {(t2) ⏐ t2 ∈ R[N] ∧ (t1,t2) ∈ R}
Примеры:
R Ia1∈ R[A](R) Ia2∈ R[A](R) I(a1,b1)∈ R[A,B](R) Ic2∈ R[C](R)
Слайд 18Операция деления (1)
Делением отношения R(M,N) на отношение S(K,L) по наборам
атрибутов N и K, которые являются совместимыми (обозначается R[N÷K)]S), называется
операция, результатом которой является отношение T(M), состоящее из таких кортежей t ∈ R[M], образы которых It(R) содержат все кортежи проекции S[K].T(M) = R[N÷K]S = {t ⏐t ∈ R[M] & It(R) ⊇ S[K]}
Позволяет формулировать запросы типа следующего:
- Вывести преподавателей, читающих ВСЕ типы лекций.
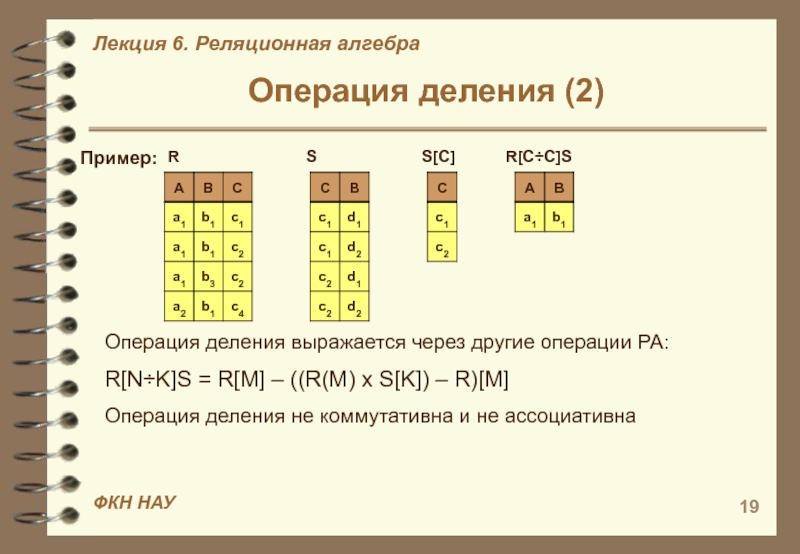
Слайд 19Операция деления (2)
Пример:
R
S
S[C] R[C÷C]SОперация деления выражается через другие операции РА:
R[N÷K]S = R[M] – ((R(M) x S[K]) – R)[M]
Операция деления не коммутативна и не ассоциативна
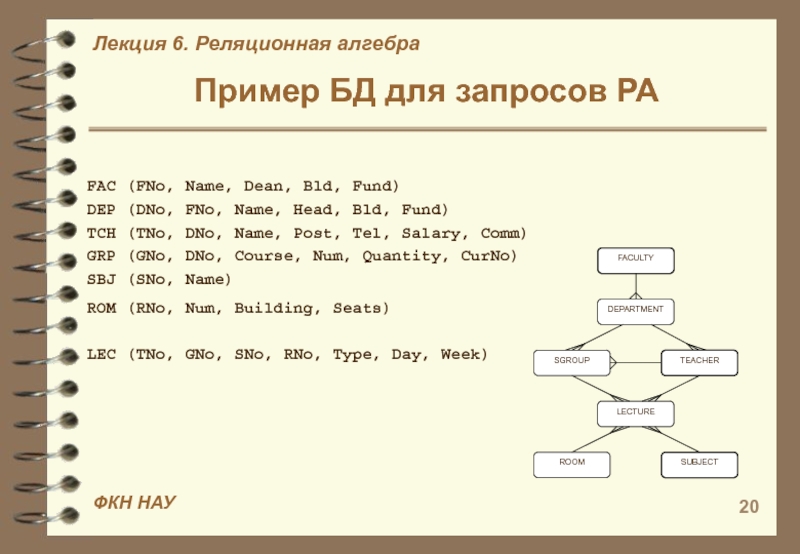
Слайд 20FAC (FNo, Name, Dean, Bld, Fund)
DEP (DNo, FNo, Name, Head,
Bld, Fund)
TCH (TNo, DNo, Name, Post, Tel, Salary, Comm)
GRP (GNo,
DNo, Course, Num, Quantity, CurNo)SBJ (SNo, Name)
ROM (RNo, Num, Building, Seats) LEC (TNo, GNo, SNo, RNo, Type, Day, Week)
Пример БД для запросов РА
Слайд 21Примеры запросов в РА (1)
Проекция: Вывести список имен преподавателей с
их должностями:
TCH[Name, Post] πName,Post(TCH)
Селекция: Вывести сведения о факультете CSF:
FAC[Name = ‘CSF’]
σName=‘CSF’(FAC)Соединение: Вывести сведения о факультетах и их кафедрах:
FAC[FNo = FNo]DEP FAC FNo=FNoDEP
Слайд 22Примеры запросов в РА (2)
Композиция соединения, селекции и проекции
1)
Вывести названия факультетов и названия их кафедр
(FAC[FNo = FNo]DEP) [FAC.Name,
DEP.Name]
πFAC.Name, DEP.Name(FAC FNo=FNoDEP)2) Вывести названия факультетов с фондом больше 1000 и названия их кафедр:
((FAC[Fund > 1000])[FNo = FNo]DEP) [FAC.Name, DEP.Name] πFAC.Name, DEP.Name((σFund >1000(FAC)) FNo=FNoDEP)
Слайд 23Примеры запросов в РА (3)
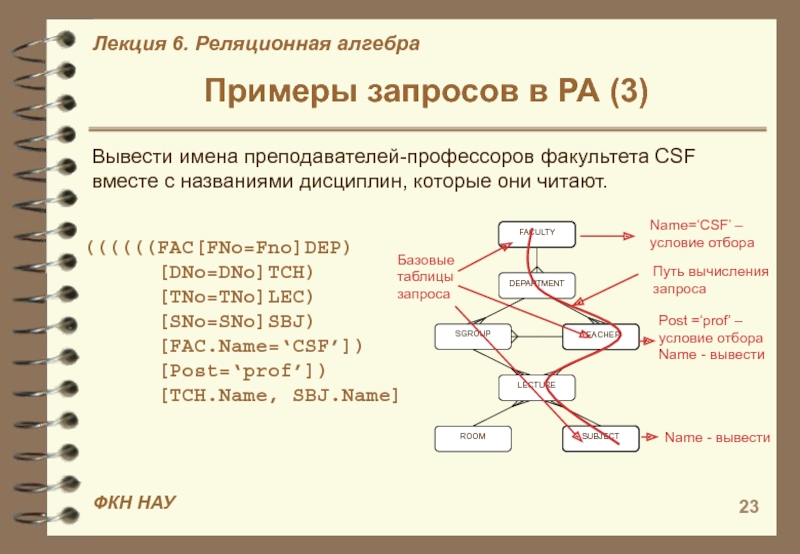
Name=‘CSF’ – условие отбора
Путь вычисления запроса
Post
=‘prof’ – условие отбора
Name - вывести
Name - вывести
Вывести имена преподавателей-профессоров
факультета CSF вместе с названиями дисциплин, которые они читают.((((((FAC[FNo=Fno]DEP)
[DNo=DNo]TCH)
[TNo=TNo]LEC)
[SNo=SNo]SBJ)
[FAC.Name=‘CSF’])
[Post=‘prof’])
[TCH.Name, SBJ.Name]
Слайд 24Примеры операции деления
1) Вывести номера преподавателей, преподающих во всех группах:
((LEC[TNo,GNo])[GNo÷GNo]GRP)[TNo]
2) Вывести номера
преподавателей, преподающих во всех
группах первого курса:
((LEC[TNo,GNo])[GNo÷GNo](GRP[Course=1]))[TNo]
3) Вывести номера преподавателей, преподающих
во всех
группах первого курса:(((LEC[TNo,GNo])[GNo÷GNo](GRP[Course=1])) [TNo=TNo]TCH)[TCH.Name]
LEC(GNo,TNo,...)
GRP(GNo, Course...)
TCH(TNo, Name...)
Слайд 25Дополнительные операции
Дополнительные операции
Присваивание
Переименование
Обобщенная проекция
Внешнее соединение
…
Слайд 26Операция присваивание
Операция присваивания (←) предоставляет удобный способ разбивать сложные запросы,
записывать запрос в виде последовательных выражений, использующих промежуточные временные отношения
и присваивания им промежуточных значений вычисления запросов.Пример: Вывести имена преподавателей, преподающих во всех группах первого курса:
(((LEC[TNo,GNo])[GNo÷GNo](GRP[Course=1])) [TNo=TNo]TCH)[TCH.Name]
Temp1 ← LEC[TNo,GNo]
Temp2 ← GRP[Course=1]
Temp3 ← Temp1[GNo÷GNo]Temp2
Temp4 ← Temp3[TNo=TNo]TCH
Temp4[TCH.Name]
Слайд 27Операция переименования
Позволяет именовать отношения вместе с их атрибутами, которые получаются
в результате вычисления выражений реляционной алгебры. Операция именования имеет следующий
синтаксис:ρR(A1,A2,...,An)(E)
Где: Е – выражение реляционной алгебры,
R(A1,A2,...,An) – имя отношения вместе с его атрибутами, которое именует отношение, полученное в результате вычисления выражения Е.
Пример: Вывести названия факультетов и названия их кафедр. Полученное отношение имеет имя FAC_DEP с именами атрибутов FName и DName соответственно:
ρFAC_DEP(FName,DName)(FAC[FNo=FNo]DEP)[FAC.Name,DEP.Name]
Слайд 28Операция обобщенной проекции
Обобщенная проекция расширяет операцию проекции, допуская включение арифметических
функций в список проецируемых столбцов.
R[F1, F2,...,Fn] πF1, F2,...,Fn(R)
Где: R –отношение или выражение
реляционной алгебрыF1, F2,...,Fn – арифметические выражения , включающие атрибуты R и константы.
Пример: Вывести имена преподавателей и их суммарную зарплату (ставка + надбавка)
TCH[Name, Salary + Commission]
Слайд 29Внешнее соединение
Внешнее соединение является расширением обычного соединения, при котором не
теряется информация определенного вида.
При внешнем соединении производится обычное соединение и
затем добавляются кортежи одного из отношений, которые не были соединены обычной операцией соединения. Слайд 30
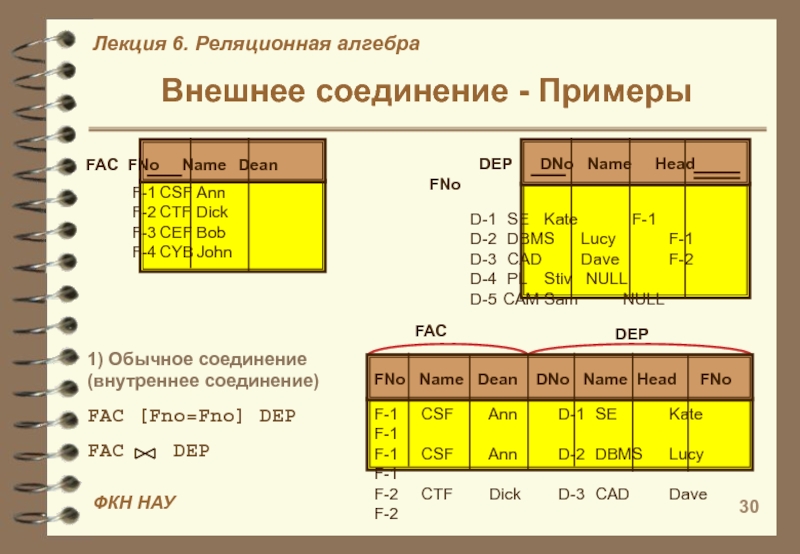
Внешнее соединение - Примеры
FAC FNo Name Dean
F-1 CSF Ann
F-2 CTF Dick
F-3 CEF Bob
F-4 CYB John
DEP DNo Name Head FNoD-1 SE Kate F-1 D-2 DBMS Lucy F-1 D-3 CAD Dave F-2 D-4 PL Stiv NULL D-5 CAM Sam NULL
1) Обычное соединение
(внутреннее соединение)
FAC [Fno=Fno] DEP
FAC DEP
FNo Name Dean DNo Name Head FNo
F-1 CSF Ann D-1 SE Kate F-1
F-1 CSF Ann D-2 DBMS Lucy F-1
F-2 CTF Dick D-3 CAD Dave F-2
FAC
DEP
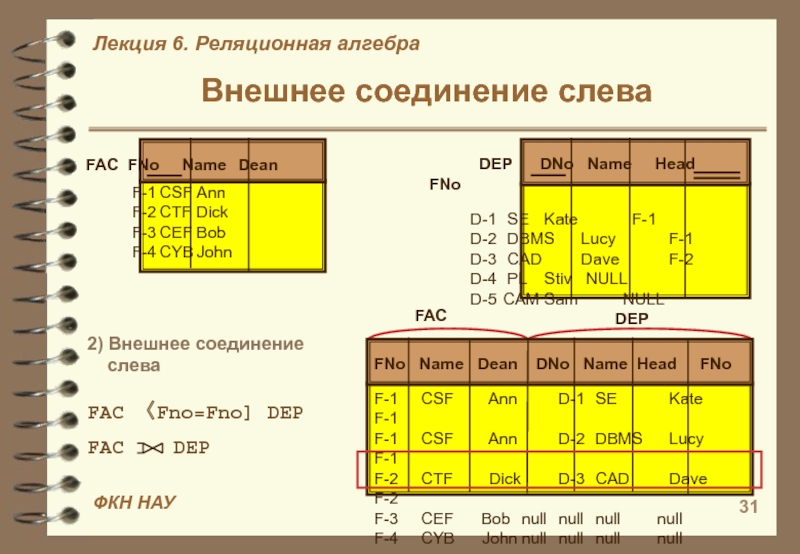
Слайд 31Внешнее соединение слева
FAC FNo Name Dean
F-1 CSF Ann
F-2 CTF Dick
F-3 CEF Bob
F-4 CYB John
DEP DNo Name Head FNoD-1 SE Kate F-1 D-2 DBMS Lucy F-1 D-3 CAD Dave F-2 D-4 PL Stiv NULL D-5 CAM Sam NULL
2) Внешнее соединение
слева
FAC 〈Fno=Fno] DEP
FAC DEP
FNo Name Dean DNo Name Head FNo
F-1 CSF Ann D-1 SE Kate F-1
F-1 CSF Ann D-2 DBMS Lucy F-1
F-2 CTF Dick D-3 CAD Dave F-2
F-3 CEF Bob null null null null
F-4 CYB John null null null null
FAC
DEP
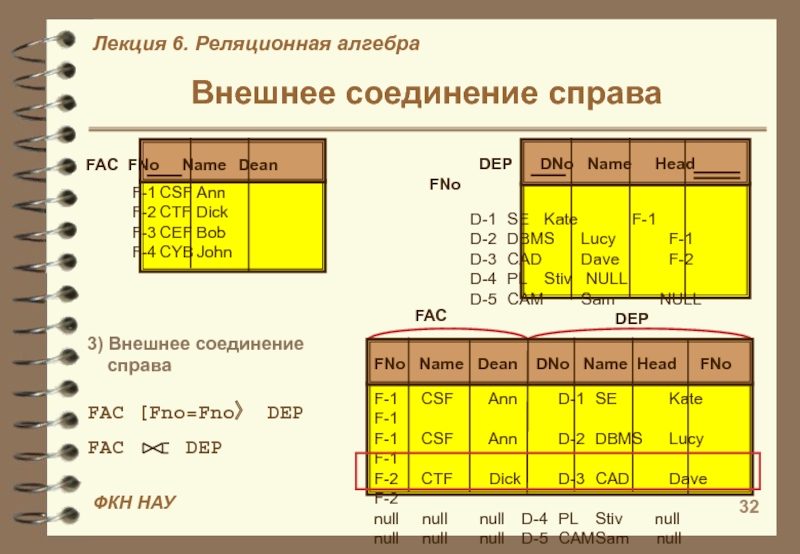
Слайд 32Внешнее соединение справа
FAC FNo Name Dean
F-1 CSF Ann
F-2 CTF Dick
F-3 CEF Bob
F-4 CYB John
DEP DNo Name Head FNoD-1 SE Kate F-1 D-2 DBMS Lucy F-1 D-3 CAD Dave F-2 D-4 PL Stiv NULL D-5 CAM Sam NULL
3) Внешнее соединение
справа
FAC [Fno=Fno〉 DEP
FAC DEP
FNo Name Dean DNo Name Head FNo
F-1 CSF Ann D-1 SE Kate F-1
F-1 CSF Ann D-2 DBMS Lucy F-1
F-2 CTF Dick D-3 CAD Dave F-2
null null null D-4 PL Stiv null
null null null D-5 CAM Sam null
FAC
DEP
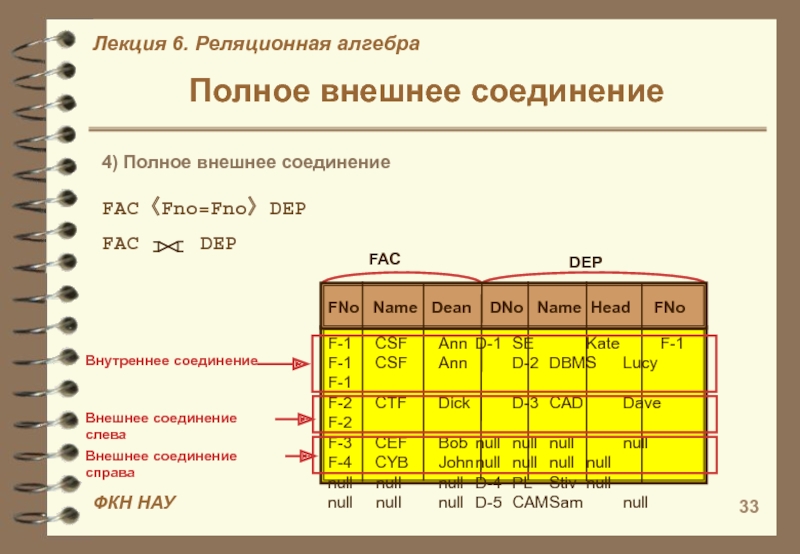
Слайд 33Полное внешнее соединение
4) Полное внешнее соединение
FAC 〈Fno=Fno〉 DEP
FAC
DEP
FNo Name Dean DNo Name
Head FNoF-1 CSF Ann D-1 SE Kate F-1 F-1 CSF Ann D-2 DBMS Lucy F-1 F-2 CTF Dick D-3 CAD Dave F-2 F-3 CEF Bob null null null null F-4 CYB John null null null null null null null D-4 PL Stiv null null null null D-5 CAM Sam null
FAC
DEP
Внутреннее соединение
Внешнее соединение слева
Внешнее соединение справа
Слайд 34Эквивалентные преобразования выражений
1) Коммутативность селекций: σF(σG(R))=σG(σF(R))=σF&G(R)
2) Коммутативность селекции и проекции:
πG(σF(R))=σF(πG(R))=σF&G(R),
если G ⊇ F
3) Дистрибутивность селекции и произведения
σF(R х S)
= σF(R) x σF(S)4) Дистрибутивность селекции с операциями над множествами:
σF(R ∪ S)=σF(R) ∪ σF(S), σF(R ∩ S)=σF(R) ∩ σF(S)
5) Дистрибутивность селекции и соединения:
σF(R S) = σF(R) S, если условие F относится к R
6) Дистрибутивность проекции с операциями над множествами:
πF(R ∪ S)=πF(R) ∪ πF(S), πF(R ∩ S)=πF(R) ∩ πF(S)
Слайд 35
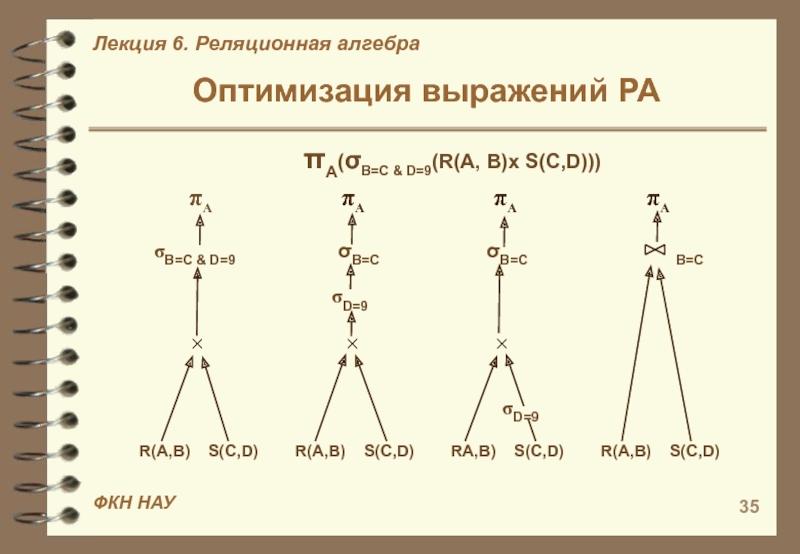
Оптимизация выражений РА
R(A,B) S(C,D) R(A,B)
S(C,D) RA,B) S(C,D)
R(A,B) S(C,D) × × ×
σD=9
σB=C & D=9 σB=C σB=C B=C
σD=9
πA
πA
πA
πA
πA(σB=C & D=9(R(A, B)x S(C,D)))
Слайд 36Общие правила оптимизации РА
Общие правила оптимизации выражений РА:
Селекции вида σF1&...&Fn(E)
предоставляются в виде
последовательности селекций σF1(... σFn(E))
Каждая из селекций
перемещается вниз по дереву
насколько это возможноРасположенные рядом селекции и декартовы произведения заменяются на соединения.
Каждая проекция перемещается по дереву вниз насколько это возможно
Каскад селекций и проекций заменяются на одну селекцию, одну проекцию или на селекцию с проекцией
Слайд 37Реляционная алгебра: выводы
Реляционная алгебра:
Формальный язык манипулирования данными в реляционной модели
Процедурный
язык, описывает как находить данные
Практически не используется в БД в
качестве ЯЗФормальная основа для оптимизации запросов
Важные термины и понятия
Объединение R ∪ S, разность R – S, пересечение R ∩ S
Проекция π<список атрибутов>(R)
Селекция σ<предикат>(R)
Декартово произведение R x S
Соединения R
Разность













![Реляционная алгебра ПолусоединениеR[М θ N)S = {(t1) ⏐ t1 ∈ R ∧ t2 ПолусоединениеR[М θ N)S = {(t1) ⏐ t1 ∈ R ∧ t2 ∈ S ∧ t1[М] θ t2[N]}Пример:R](/img/thumbs/b6fbc334ce4844be39e6a7b1c2623085-800x.jpg)
![Реляционная алгебра Образ кортежаОбразом реляционного отношения R(M,N) относительно кортежа кортежа t1 ∈ R[M], Образ кортежаОбразом реляционного отношения R(M,N) относительно кортежа кортежа t1 ∈ R[M], изображаемым как It1(R), называется такое множество](/img/thumbs/6d404885a09f951cce829a4188a4862e-800x.jpg)

![Реляционная алгебра Примеры запросов в РА (1)Проекция: Вывести список имен преподавателей с их Примеры запросов в РА (1)Проекция: Вывести список имен преподавателей с их должностями: TCH[Name, Post] πName,Post(TCH)Селекция: Вывести сведения о факультете](/img/thumbs/63e9bf0dab76bfe4b17b2f8c599dc72d-800x.jpg)

![Реляционная алгебра Примеры операции деления1) Вывести номера преподавателей, преподающих во всех группах: ((LEC[TNo,GNo])[GNo÷GNo]GRP)[TNo]2) Вывести номера преподавателей, Примеры операции деления1) Вывести номера преподавателей, преподающих во всех группах: ((LEC[TNo,GNo])[GNo÷GNo]GRP)[TNo]2) Вывести номера преподавателей, преподающих во всех группах первого](/img/thumbs/53338b6b72224f21eedcf97a77f967c8-800x.jpg)



![Реляционная алгебра Операция обобщенной проекцииОбобщенная проекция расширяет операцию проекции, допуская включение арифметических функций Операция обобщенной проекцииОбобщенная проекция расширяет операцию проекции, допуская включение арифметических функций в список проецируемых столбцов. R[F1, F2,...,Fn] πF1,](/img/thumbs/2c6b316af504af6fcb478e631bec919a-800x.jpg)