Введение в анализ данных при проведении исследования

(данных наблюдений, измерений, экспертных оценок и т.д.)
Анализ данных используется на

различных этапах проведения исследования (как правило, во второй и третьей главе диссертаций), необходим для практического подтверждения гипотезы исследования.
Анализ данных – научное направление, включающее в себя многочисленные подходы и алгоритмы (data mining)

после их сбора?
Очистка и предобработка данных
Фильтрация данных
Сортировка данных
Перекодирование данных (создание

категориальных переменных из количественных)
Пропуски в данных и борьба с ними
Выявление аномальных данных
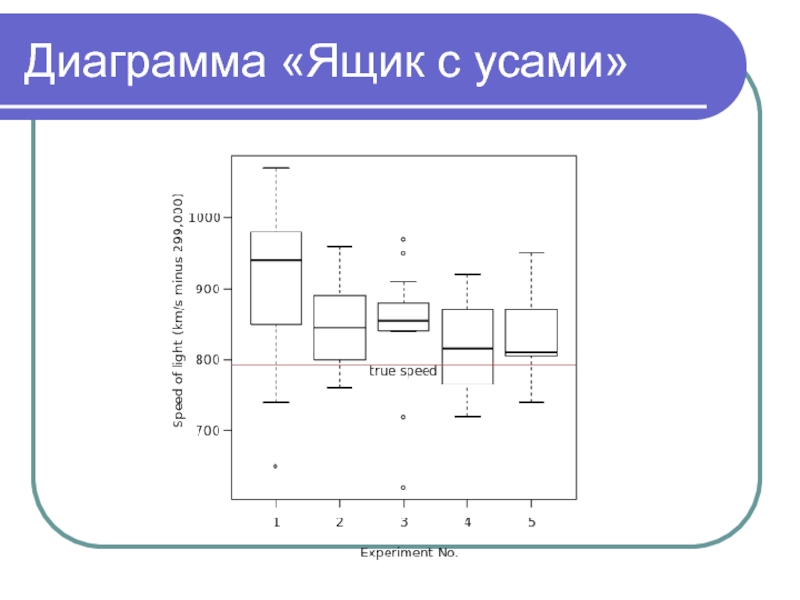
Построение диаграмм (столбиковых, круговых, ящиковых, интерактивных)
// P.S. Подробная информация в соответствующей литературе (например, Аббакумов В. Л., Лезина Т.А. Бизнес-анализ информации. Статистические методы. – М. : Экономика, 2009. – 373 с. )

объектов.
Генеральная совокупность – совокупность всех объектов, из которых производится выборка.
Объем

совокупности – число объектов в этой совокупности.
Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной. Выборка будет репрезентативной при обследовании большой группы людей, если внутри этой группы есть представители разных подгрупп, только так можно сделать верные выводы.

произведений всех возможных значений случайной величины на соответствующие им вероятности

(понятие среднего значения случайной величины)
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания (мера разброса данной случайной величины, то есть её отклонения от математического ожидания )
Средним квадратическим отклонением случайной величины называется корень квадратный из ее дисперсии (наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. Используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами)

интервал — термин, используемый при интервальной (в отличие от точечной) оценке статистических

параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины

в совокупности
Медиана – значение признака у статистической единицы, стоящей в

середине ранжированного ряда и делящей совокупность на 2 равные по численности части
Квартили – значения признака, делящие упорядоченную совокупность на 4 равные части
Гистограмма в математической статистике - это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него.

статистическими данными
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой

статистической информации.
Любое статистическое наблюдение предполагает получение данных, которые будут полно и точно отражать действительность.
В процессе проведения статистического наблюдения могут возникать погрешности, которые приводят к снижению достоверности статистического наблюдения.
Основное требование, которое предъяввляется к статистическому наблюдению – это точность статистических данных.

значения какого-либо признака или показателя, который был получен вследствие статистического

наблюдения, действительному его значению. В процессе подготовки и проведения статистического исследования, чтобы предупредить возможность появления отклонений или разности между исчисленными показателями, нужно предусмотреть и осуществить ряд мероприятий. Если же такие отклонения возникли, их называют ошибками статистического наблюдения.
Материалы, собранные в результате наблюдения, подвергаются всесторонней проверке и контролю. Они проверяются с точки зрения полноты охвата всех единиц совокупности наблюдения и правильности заполнения документов и в порядке логического и арифметического контроля.

ошибки репрезентативности и ошибки регистрации.
Ошибки репрезентативности показывают, в какой степени выборочная

совокупность представляет генеральную совокупность. Эти ошибки возникают потому, что наблюдению подвергается только часть единиц изучаемой совокупности, и сведения эти не могут абсолютно точно отобразить свойства всей массы явлений совокупности.
Возникающие в результате неправильного установления фактов ошибки регистрации можно подразделить на:
1) случайные – это ошибки, которые могут дать искажения как в одну, так и в другую сторону;
2) систематические ошибки, возникающие вследствие нарушения принципов непреднамеренного отбора единиц изучаемой совокупности. Систематические ошибки опасны, потому что они влияют на полученные итоговые показатели;
3) преднамеренные ошибки возникают вследствие умышленного искажения фактов.

Здесь выбор отдельных единиц осуществляется либо по жребию, путем подбрасывания

монет или игральной кости и т. д., либо путем использования таблиц случайных чисел. При этом каждая единица совокупности имеет равную возможность попасть в выборку. Это обеспечивает Достаточную близость средней выборочной величины к средней генеральной величине. Этот вид отбора ввиду его громоздкости сравнительно редко используется.
2. Механический отбор. Здесь единицы совокупности выбираются в определенном, формально установленном порядке. Например, желая исследовать распределение гласных, мы нумеруем все фонемы текста, после чего фиксируем присутствие или отсутствие гласной во всех фонемных позициях, номер которых кратен 10 (или 5, 3 и т. п.).

выборки, где отбор каждой единицы проводится в индивидуальном порядке, серийная

выборка предполагает отбор сериями. Эти серии отбираются в случайном порядке, чаще бесповторным способом. Отобрав таким образом серии, исследователь проводит внутри их сплошное наблюдение. 4. Типический отбор. Это способ, при котором исследуемая статистическая совокупность разбивается по существенному, типическому признаку на качественно однородные, однотипные группы, затем из каждой этой группы случайным способом отбирается определенное количество единиц, пропорциональное удельному весу группы во всей совокупности.
Типический отбор дает более точные результаты, так как при нем в выборку попадают представители всех типических групп.