Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления
Содержание
- 1. Системы счисления
- 2. Содержание: Общие сведения о системах счисления. "Машинная
- 3. Система счисления – это определенный
- 4. «Мыслю,следовательно,существую». Р.ДекартСтраницы истории ЦивилизацияАцтеков и майяВавилонская цивилизация Египетская цивилизация Римская цивилизация
- 5. Глиняные таблички, найденные в Месопатамии с культурным
- 6. Система счисления вавилонян (на основе позиционного принципа)
- 7. Система счисления египтянИероглифическая система счисления имеет основание
- 8. Система счисления ацтеков и майяУ ацтеков и
- 9. Римская система счисленияДо нас дошла римская система
- 10. Системы счисленияНепозиционныеПозиционныеВиды систем счисления
- 11. Непозиционные системы счисления Непозиционной называется такая система
- 12. Пример 1. У
- 13. Пример 2.Египтяне для записи чисел применяли иероглифы.
- 14. I – 1; V – 5; X
- 15. Непозиционные системы счисления Непозиционные
- 16. Позиционные системы счисления "Мысль выражать все числа
- 17. Впервые идея позиционной системы счисления возникла в Древнем Вавилоне.Позиционные системы счисления
- 18. Позиционные системы счисления Множество цифр,
- 19. Основные достоинства любой позиционной системы счисления:простота выполнения
- 20. Пример:239,4510 = 2×102 + 3×101 + 9×100
- 21. Позиционные системы счисления Перевод целых десятичных чисел в другие системы счисления.
- 22. Позиционные системы счисления Перевод дробных десятичных чисел в другие системы счисления.0,187510= 0,00112=0,148 = 316
- 23. Перевод смешанных десятичных чисел в другие системы счисления.Позиционные системы счисления +11,187510= 1011,00112
- 24. "Машинные" системы счисления ДвоичнаяВосьмеричнаяШестнадцатеричная
- 25. для ее реализации нужны технические устройства
- 26. "Машинные" системы счисления Таблицы перевода чисел в машинной группе.
- 27. "Машинные" системы счисления Перевод чисел в машинной группе."Машинные" системы счисления
- 28. Все фантастические возможности вычислительной техники реализуются путем
- 29. Правила выполнения арифметических действий над двоичными числами
- 30. Теперь предлагаем еще раз ответить на вопрос
- 31. Практические задания по теме «Системы счисления»1. Какие
- 32. Слайд 32
- 33. 6. Запишите в развернутом виде числа: а)
- 34. 9. Какое минимальное основание имеет система счисления,
- 35. 13. Выпишите целые десятичные числа, принадлежащие следующим
- 36. Скачать презентанцию
Содержание: Общие сведения о системах счисления. "Машинная группа" систем счисления. Перевод чисел в позиционных системах счисления .
Слайды и текст этой презентации
Слайд 3 Система счисления – это определенный способ записи чисел
и соответствующие правила действия над числами.
Системы счисления
Числа не управляют
миром, но показывают, как управляется мир.
И.-В. Гете
Слайд 4«Мыслю,следовательно,существую».
Р.Декарт
Страницы истории
Цивилизация
Ацтеков и майя
Вавилонская
цивилизация
Египетская
цивилизация
Римская
цивилизация
Слайд 5Глиняные таблички, найденные в Месопатамии с культурным центром -
г.Вавилон.
Около 1700 г. до н.э.
Вавилонская система счисления :
является комбинацией шестидесятеричной
и десятичной систем с применением позиционного принципа;используется всего два символа для обозначения числа 1 и числа10 .
шестидесятеричной системой пользуются до сих пор при измерении времени и углов.
Слайд 7Система счисления египтян
Иероглифическая система счисления имеет основание 10 и не
является позиционной: для обозначения чисел 1, 10, 100 и т.д.
в ней используются разные символы, каждый символ повторяется определенное число раз, и, чтобы прочитать число, нужно просуммировать значения всех символов, входящих в его запись. Таким образом, их порядок не играет роли, и они записываются либо горизонтально, либо вертикально.
Слайд 8Система счисления ацтеков и майя
У ацтеков и майя, населявших американский
континент и создавших там высокую культуру, почти полностью уничтоженную
испанскими
завоевателями в XVI - XVII в., была принятадвадцатеричная система счисления.
Та же система была принята у кельтов, населявших Западную Европу, начиная со II тысячелетия до нашей эры.
Слайд 9Римская система счисления
До нас дошла римская система записи чисел, которая
в некоторых случаях применяется в нумерации (века, тома в собрании
сочинений и др.). В римской системе в качестве цифр используются латинские буквы:I V X L C D M
1 5 10 50 100 500 1000
Эта система непозиционная. В ней цифры записываются слева направо. Если слева записана меньшая цифра, а справа - большая, то их значения вычитаются. Наоборот - складываются.
Слайд 11Непозиционные системы счисления
Непозиционной называется такая система счисления, в которой
от положения цифры в записи числа не зависит величина, которую
она обозначает.
Слайд 12Пример 1.
У многих народов использовалась
система, алфавит которой состоял из одного символа — палочки. Для
изображения какого-то числа в этой системе нужно записать определенное множество палочек, равное данному числу: ||||| — число пять.Непозиционные системы счисления
Слайд 13Пример 2.
Египтяне для записи чисел применяли иероглифы.
|- единица, ∩ - десяток, - сотня
Например, 345: ∩ ∩ ∩ ∩ | | | | |.Непозиционные системы счисления
Слайд 14I – 1; V – 5; X – 10; L
– 50; C – 100;
D – 500; M – 1 000
Например, II — два, III — три,
XXX — тридцать, CC — двести,
VII — семь, IX — девять.
Пример 3.
Римские числа, их и сейчас можно увидеть во многих местах, например на циферблате кремлевских курантов, – главных часов России.
Непозиционные системы счисления
Слайд 15Непозиционные системы счисления
Непозиционные системы счисления имеют
ряд недостатков:
Для записи больших чисел приходиться вводить новые цифры.
2.
Невозможно записывать дробные и отрицательные числа.3. Сложно выполнять арифметические операции.
Слайд 16Позиционные системы счисления
"Мысль выражать все числа немногими знаками, придавая
им, кроме значения но форме, еще значение по месту, настолько
проста, что именно из-за этой простоты трудно оценить, насколько она удивительна".П.-С. Лаплас
Позиционной называется такая система счисления, в которой величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Слайд 17Впервые идея позиционной системы счисления возникла в Древнем Вавилоне.
Позиционные системы
счисления
Слайд 18Позиционные системы счисления
Множество цифр, используемых для
изображения чисел в данной системе счисления, - алфавит.
Количество различных цифр, используемых для изображения чисел в данной системе счисления, - основание.Место каждой цифры в числе – позиция.
Слайд 19Основные достоинства любой позиционной системы счисления:
простота выполнения арифметических операций;
ограниченное количество
символов, необходимых для записи любого числа.
Позиционные системы счисления
Слайд 20Пример:
239,4510 = 2×102 + 3×101 + 9×100 + 4×10-1 +
5×10-2
Позиционные системы счисления
Развернутая форма записи числа.
q - основание системы
счисления,
n - число разрядов целой части числа,m - число разрядов дробной части числа, ai - цифра числа, Aq - само число.
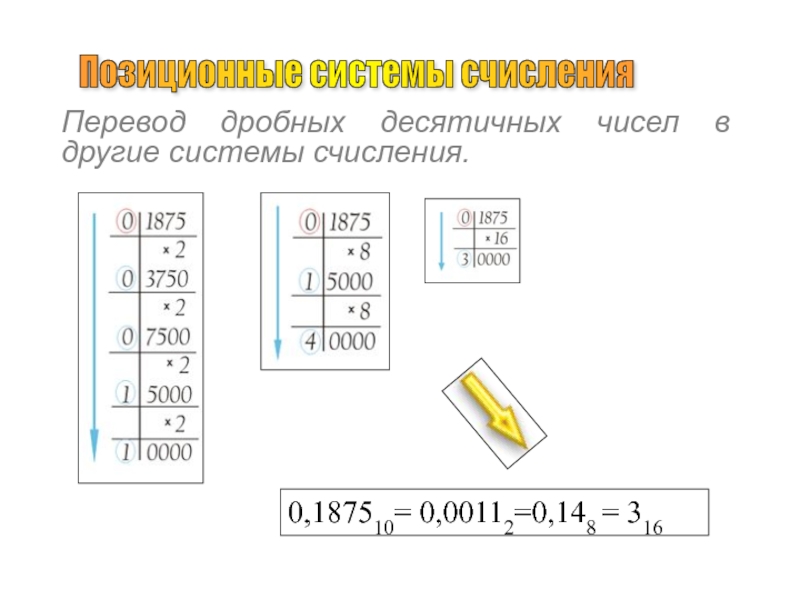
Слайд 22Позиционные системы счисления
Перевод дробных десятичных чисел в другие системы
счисления.
0,187510= 0,00112=0,148 = 316
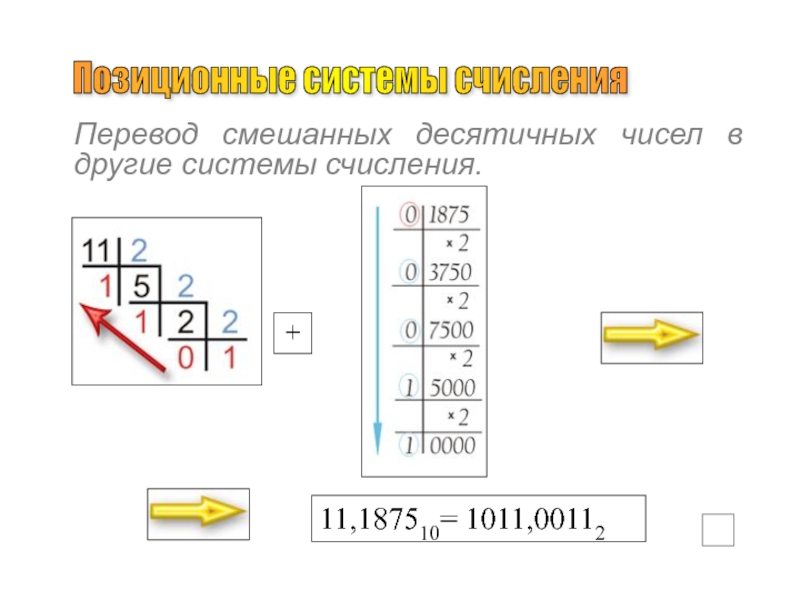
Слайд 23Перевод смешанных десятичных чисел в другие системы счисления.
Позиционные системы счисления
+
11,187510= 1011,00112
Слайд 25
для ее реализации нужны технические устройства с двумя устойчивыми
состояниями;
представление информации посредством только двух состояний надежно и
помехоустойчиво; возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика проще десятичной.
Недостаток двоичной системы —
быстрый рост числа разрядов, необходимых для записи чисел.
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
Слайд 28 Все фантастические возможности вычислительной техники реализуются
путем создания разнообразных комбинаций
сигналов высокого и низкого уровней.
“Единица” условно обозначает включенное состояние,
а “нуль” - выключенное состояние.Поэтому не будем недооценивать роль единицы и нуля, особенно,
если речь идет о двоичной системе счисления.
Слайд 29Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения,
вычитания и умножения.
Сложение Вычитание Умножение
0 + 0 = 0 0 - 0 =
0 0 * 0 = 0
0 + 1 = 1 1 - 0 = 0 0 * 1 = 1
1 + 0 = 1 1 - 1 = 0 1 * 0 = 1
1 + 1 = 10 10 - 1 = 1 1 * 1 = 1
Операция умножения многоразрядных двоичных чисел внутри ЭВМ сводится к операции сдвига и сложения.
Слайд 30Теперь предлагаем еще раз ответить на вопрос :
сколько же будет
2*2 ?
В двоичной,
в троичной,
в четверичной
и других системах счисления?
Слайд 31Практические задания по теме «Системы счисления»
1. Какие числа записаны римскими
цифрами:
а) MCMXCIX; б) CMLXXXVIII; в) MCXLVII?
2.
Запишите год, месяц и число своего рождения c помощью римских цифр. 3. Некоторые римские цифры легко изобразить, используя палочки или спички. Ниже написано несколько неверных равенств. Как можно получить из них верные равенства, если разрешается переложить с одного места на другое только одну спичку (палочку)?
VII - V=XI IX-V=VI
VI - IX=III VIII - III=X
Слайд 336. Запишите в развернутом виде числа:
а) А8=143511; б) А2=100111;
в) А16=143511;
г) А10=143,511;
д) А8=0,143511;
е) А16=1A3,5C1.
7. Запишите в свернутой
форме следующие числа: а) А10= 9·101+1·100+5·10-1+3·10-2;
б) А16=А·161+1·160+7·16-1+5·16-2.
8. Правильно ли записаны числа в соответствующих системах счисления:
а) А10=А,234;
б) А8=-5678;
в) А16=456,46;
г) А2=22,2;
Слайд 349. Какое минимальное основание имеет система счисления, если в ней
записаны числа 127, 222, 111? Определите десятичный эквивалент данных чисел
в найденной системе счисления.10. Чему равен десятичный эквивалент чисел 101012, 101018 1010116?
11. Какое из чисел 1100112, 1114, 358 и 1В16 является: а) наибольшим; б) наименьшим.
12. Существует ли треугольник, длины сторон которого выражаются числами 128, 1116 и 110112?
Слайд 3513. Выпишите целые десятичные числа, принадлежащие следующим числовым промежуткам:
а)
[1011012; 1100002]; б) [148; 208]; в) [2816; 3016].
14.
В классе 11112 девочек и 11002 мальчиков. Сколько учеников в классе? 15. У меня 100 братьев. Младшему 1000 лет, а старшему 1111 лет. Старший учится в 1001 классе. Может ли такое быть?
![13. Выпишите целые десятичные числа, принадлежащие следующим числовым промежуткам: а) [1011012; 1100002]; б) [148; 208]; в) [2816;](/img/thumbs/e539aa1ec258223f3cf2de11d8728761-800x.jpg "Системы счисления 13. Выпишите целые десятичные числа, принадлежащие следующим числовым промежуткам: а) [1011012;")
