Комплексные числа

а и b – действительные числа, а i – некоторый

символ такой, что



Действительное число a называется действительной частью z=a+bi (Re z), а число b-мнимой частью (Im z)

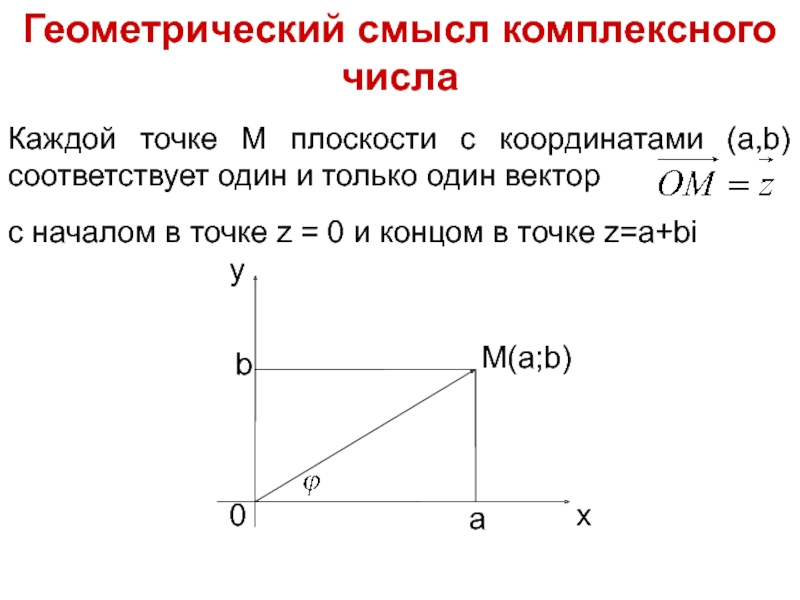
Комплексное число z=a+bi изображают точкой плоскости с координатами (a;b)
Точка М(a;b), соответствующая комплексному числу z=a+bi, называется аффиксом данного числа z.

если а = с и b = d.

Комплексное число a-bi

называется
комплексно сопряженным с числом a+bi
и обозначается через
= a-bi

Комплексные числа вида a+bi и –a-bi называются противоположными.

b) и
w = (c; d) называется комплексное число
(a+c;

b+d).
Разностью комплексных чисел z = (a; b) и w = (c; d) называют такое числоu, которое в сумме с числом w даёт число z
z = w + u.

– c; b – d).
Произведением комплексных чисел z = (a;

b) и
w = (c; d) называют комплексное число
(ac – bd; ad + bc)

Частным от деления z на w называют число u, равное:

u

на 4, то значение степени равно 1, если при делении

показателя на 4 в остатке получается 1, то значение степени равно i, если при делении показателя на 4 остаток равен 2, то значение степени равно -1, если в остатке при делении показателя на 4 будет 3, то значение степени равно –i.

i216 ,4)i137
Решение:
1) i66

66:4=16(2). Остаток равен 2, значит i66=-1

2)i143
143

:4=35(3).В остатке 3, значит i 143=-i

3)i216
216:4=54(0).в остатке 0, значит i216=1

4)i137

137:4=34(1).В остатке 1, значит i137=i

,

соответствует один и только один вектор
с началом в точке z

= 0 и концом в точке z=a+bi

y

x

M(a;b)

0

b

a

плоскости xOy, то модуль Z равен расстоянию точки M (a,b)

от начала координат


Если на плоскости ввести полярные координаты (r,φ), где φ аргумент числа z (φ=argz) - угол между действительной осью ОХ и вектором ОМ, то а = r COS φ, b = r SIN φ
В силу этого комплексное число Z можно записать в форме z = r(COS φ+iSIN φ),
где r – модуль числа Z, φ – угол (в рад.), который составляет вектор OM с положительным направлением оси ox

в виде:
z = r(cosφ + isinφ), где

- модуль, а
φ – аргумент числа z, связанный с а и b формулами:

Угол φ из промежутка называется главным аргументом. Все остальные значения угла φ могут быть получены прибавлением к главному аргументу значений 2 n, где n – любое целое число.

Сначала находим модуль числа:

Далее, согласно формулам (*),

имеем:

Учитывая, что угол

Итак,

чисел, заданных в тригонометрической форме, их модули перемножаются /делятся, а

аргументы складываются (вычитаются).

(1)

(2)

Используя формулу (1), находим:

в натуральную степень n
модуль данного числа возводится в эту степень,
а

аргумент умножается на показатель степени:

формула Муавра

из комплексного числа z = r (Cosφ + iSinφ) имеет

n различных значений, которые находятся по формуле :

Здесь к = 0, 1, 2, … n-1

Корнями данного уравнения являются все значения

Для числа - 4 имеем r =2,
Согласно формуле(3),
находим:

Если к = 0, то

Если к = 1, то

Если комплексному числу
, модуль которого равен 1, поставить в

соответствие
показанное выражение

, то получим соотношение

то получим соотношение которое называется формулой Эйлера.
Любое комплексное число

можно записать в виде

. Эта форма записи комплексного числа называется показательной формой.

тогда

показательная форма числа имеет вид
.

показательной форме.

Решение. Что бы представить число
в виде

нужно найти модуль и аргумент числа

.

Здесь

тогда

так как точка

лежит на мнимой оси комплексной плоскости.

Зная r и

, получим

.

записаны в показательной форме, то умножение, деление, возведение в степень

производится по правилам действий со степенями.

Так, для произведения и частного комплексных чисел

и

справедливы формулы

а для n-й степени комплексного числа используется

формула

n значений: 0,1,2,…,n-1.

– некоторая область на комплексной плоскости
Определение. Функцией комплексного аргумента

с областью определения D называется соответствие,которое любому комплексному числу сопостовляет одно или несколько комплексных значений.
Таким образом, в отличие от действительного анализа, в комплексном анализе допускаются многозначные функции. Например,

f(z)=az+b (a, b – фиксированные комплексные числа)-однозначная функция;
- однозначная функция

- n-значная функция;

-бесконечнозначная функция.
Если функция однозначна,то она может быть задана в виде отображения В таком случае функция называется однолистной .В дальнейшем, если не указано особо,будем рассматривать однолистные функции.

найти

Решение: Подставим в место z значение i в функцию





Ответ: f(i)=1

Представим z в алгебраической

форме Значение f(x)-комплексное число,т.е. ,которое также можем представить в алгебраической форме ,где и -действительные функции комплексного аргумента,но задание я эквивалентно заданию пары(x,y).Окончательно,любую функцию комплексного аргумента можно представить в виде
,где и -действительные функции двух действительных переменных.Функции u и v называются компонентами функции f(z),u- действительная компонента,v-мнимая компонента.Пишут :

найти ее действительную и мнимую часть.
Решение:
(x+iy)2+4i=x2+2ixy-y2+4i=(x2-y2)+(2xyi+4i)=(x2-y2)+i(2xy+4).

Тогда действительная часть функции f(z) - x2-y2,а
мнимая - 2xy+4.

Так как это определение формально совпадает с обычным ,то все свойства непрерывной функции комплексного аргумента совпадают дословно со свойствами действительных функций.