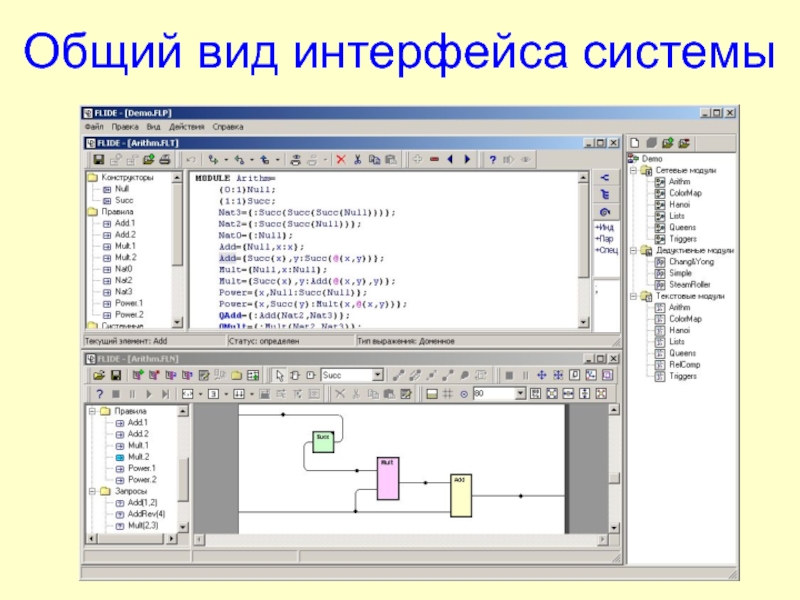
Кутепов В.П.).
Имеет развитые средства схемного описания НО.
Допускает использование:
индексированных имен НО,
параметризованных
НО.Поддерживает объектно-ориентированный стиль программирования.
Позволяет строить многомодульные программы.
Обладает средствами ограничения области видимости определяемых отношений (Private-домены).








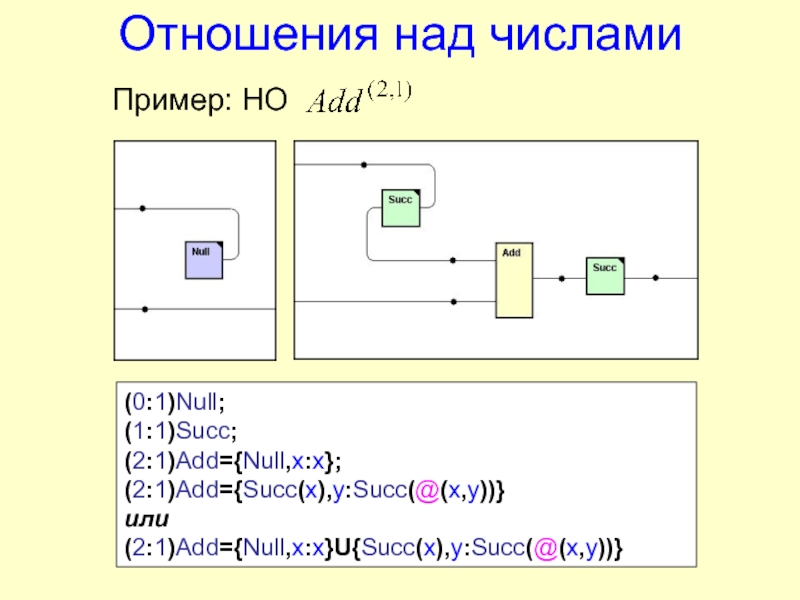
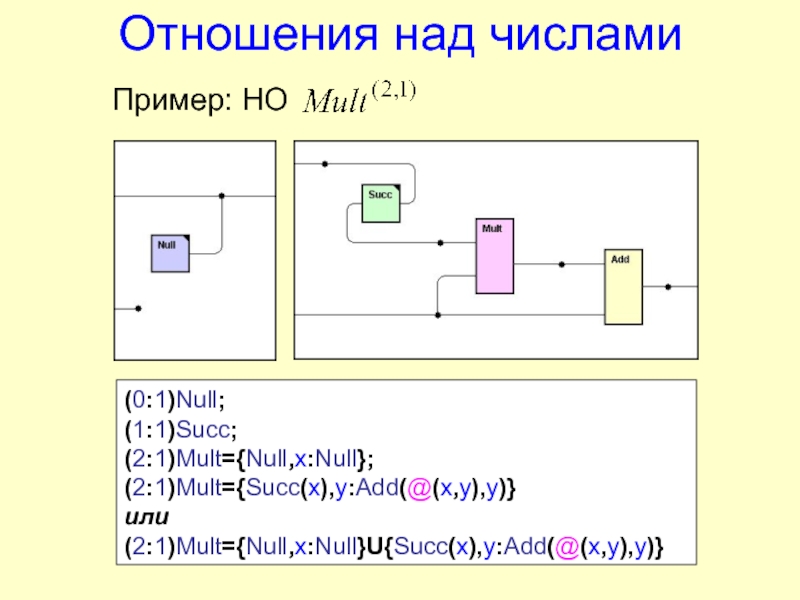
![FLIDE Система функционально-логического программирования на языке S-FLOGOL СпискиПример: НО (0:1)Nil;(1:1)LCons;(0:1)A;(0:1)B;(0:1)C;(0:1)D;(0:1)List={:LCons(A,LCons(B,LCons(C,LCons(D,Nil)))}[A,B,C,D] СпискиПример: НО (0:1)Nil;(1:1)LCons;(0:1)A;(0:1)B;(0:1)C;(0:1)D;(0:1)List={:LCons(A,LCons(B,LCons(C,LCons(D,Nil)))}[A,B,C,D]](/img/thumbs/7cdddc87dfaa443830c806beeac16144-800x.jpg)

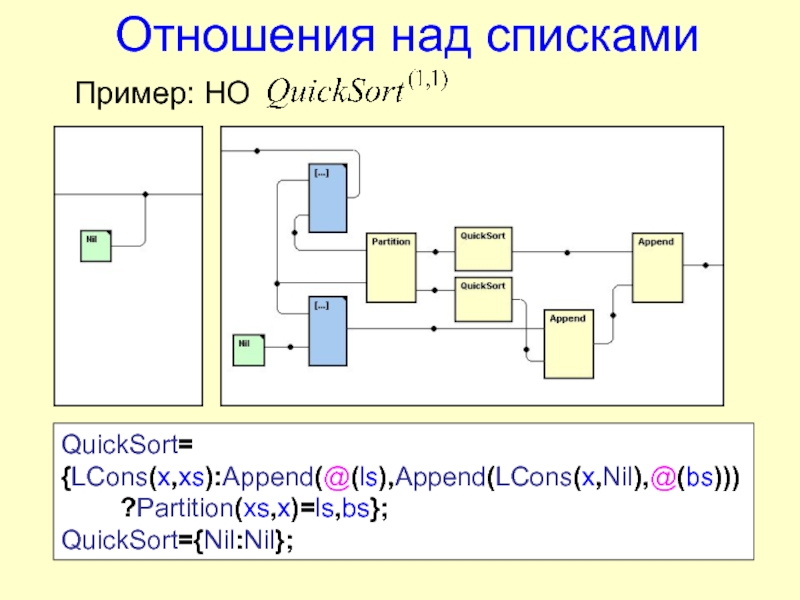
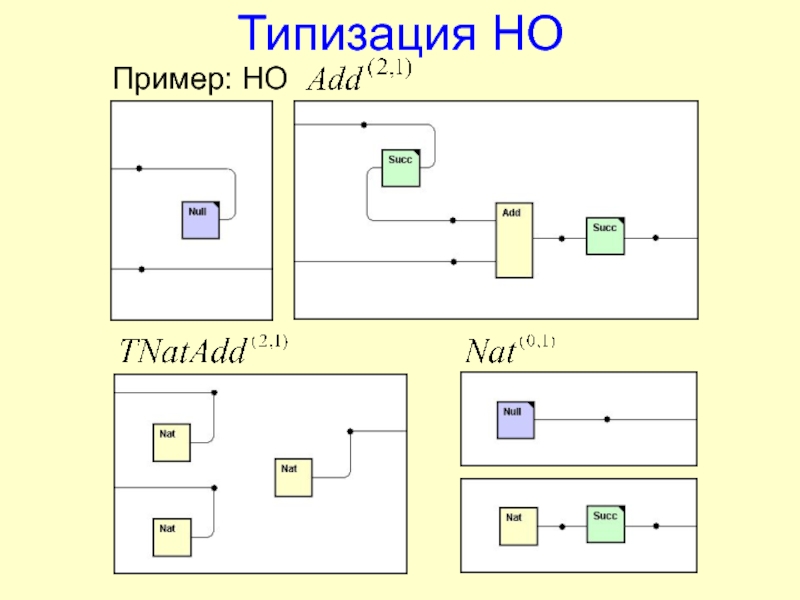
![FLIDE Система функционально-логического программирования на языке S-FLOGOL Индексированные имена НОПример: множество натуральных чисел(I=1..)[I]Nat= Null∙(∙ J=1..I)SuccЭквивалентное множество определений:[0]Nat= Null;[1]Nat= Null∙Succ;[2]Nat= Null∙Succ∙Succ;[3]Nat= Null∙Succ∙Succ∙Succ;… Индексированные имена НОПример: множество натуральных чисел(I=1..)[I]Nat= Null∙(∙ J=1..I)SuccЭквивалентное множество определений:[0]Nat= Null;[1]Nat= Null∙Succ;[2]Nat= Null∙Succ∙Succ;[3]Nat= Null∙Succ∙Succ∙Succ;…](/img/thumbs/68347d3cf27b78a5536104666750a73a-800x.jpg)
![FLIDE Система функционально-логического программирования на языке S-FLOGOL Параметризованные НОMap={LCons(x,xs):LCons(«0»(x),@(xs))};Map={Nil:Nil};SuccList = Map[Succ]Пример:НО(инкрементация элементов списка) Параметризованные НОMap={LCons(x,xs):LCons(«0»(x),@(xs))};Map={Nil:Nil};SuccList = Map[Succ]Пример:НО(инкрементация элементов списка)](/img/tmb/2/145518/076b62ea9e5391b78e15b7be73a091bc-800x.jpg)


![FLIDE Система функционально-логического программирования на языке S-FLOGOL Системные типы данныхНатуральные числа (0,1,2,…).Списки ([ ], [A(B),[D]]).Строки (‘Some text’).Пример записи Системные типы данныхНатуральные числа (0,1,2,…).Списки ([ ], [A(B),[D]]).Строки (‘Some text’).Пример записи списка [A,B,C] в сетевой форме при](/img/tmb/2/145518/24e3e7e40cfc83fd3707b51353522fd9-800x.jpg)