резонатора была решена
Фоксом и Ли в 1961 году методом
последовательных приближений при многократных проходах первоначально плоской волны через резонатор
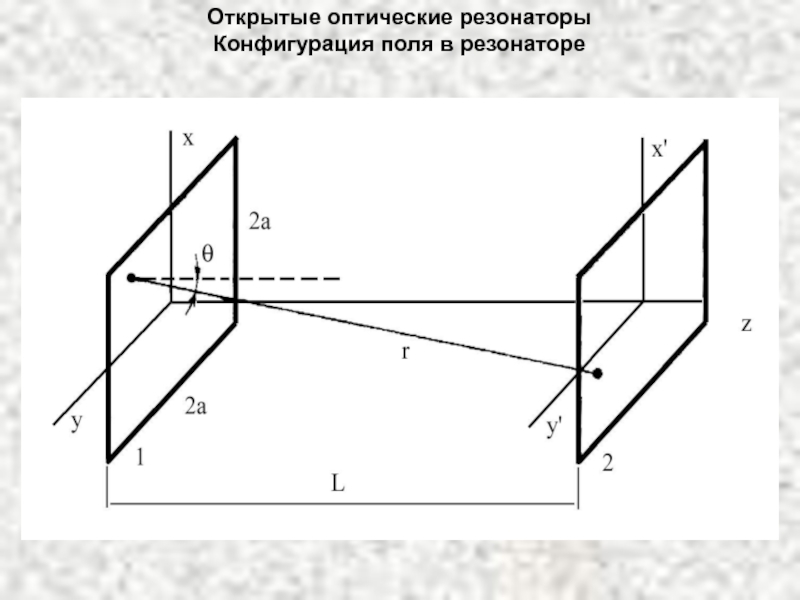
Распределение поля на поверхности левого зеркала служит источником поля, возникающего у правого зеркала. Полученное распределение поля на правом зеркале используется для ычисления
распределения поля вновь у левого зеркала. Эти вычисления повторяются многократно.
При расчете используется принцип Гюйгенса: каждый элемент поверхности одного зеркала рассматривается как источник сферической волны, при этом поле на поверхности другого зеркала является результатом суперпозиции этих волн
Использование этого метода допустимо в том случае, когда размеры зеркал
резонатора велики по сравнению с длиной волны излучения, а поле близко
к поперечному, что хорошо выполняется в резонаторе