Средние величины

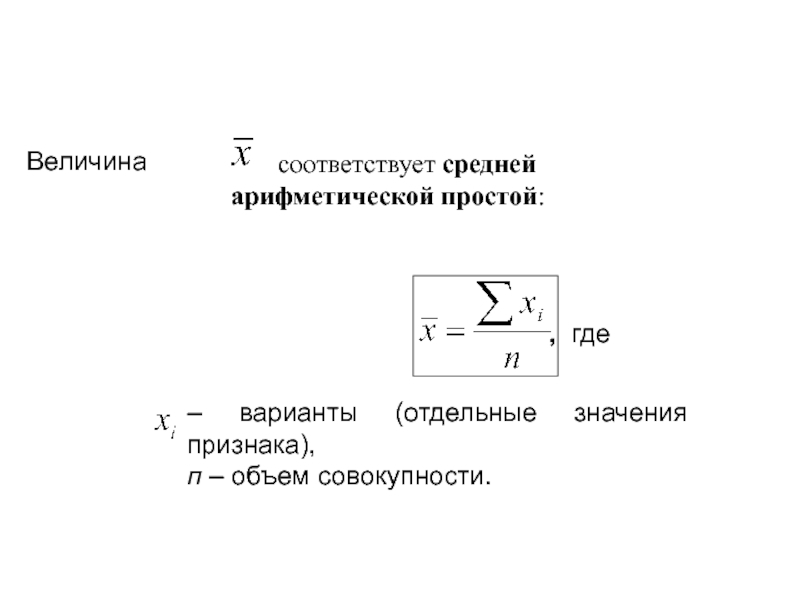
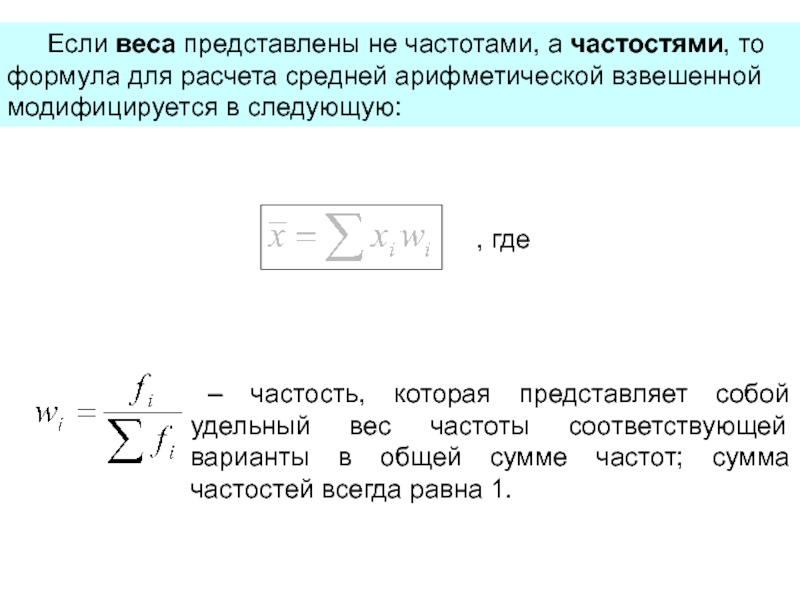
максимальным значениями признака достаточно невелик или же характер изменения данных

при переходе от одной варианты к другой приближенно можно свести к правилу арифметической прогрессии.

Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина.
Пример.
Имеются данные о величине рентабельности по десяти малым предприятиям (%):
10, 12, 12, 15, 15, 15, 17, 17, 20, 20.
Средняя рентабельность составит:

значения признака),
п – объем совокупности.

расчета средней арифметической взвешенной модифицируется в следующую:
, где
– частость,

которая представляет собой удельный вес частоты соответствующей варианты в общей сумме частот; сумма частостей всегда равна 1.

не известны значения частот у вариант ряда, но имеются для

каждого xi произведения этих вариант на соответствующие им частоты, т.е.

Величиной Fi может быть товарооборот по видам товаров при расчете средней их цены; фонды заработной платы у отдельных категорий работников при расчете средней заработной платы; стоимостные объемы сделок при покупке валют, ценных бумаг, биржевых продажах и т.д.

произведения варианты на соответствующую ей частоту.

цену одной акции:

(при этом мы можем их не знать, но известно об

их равенствах), т.е.

, то применяется средняя гармоническая простая

, где п – объем совокупности.

Пример
Предприятием были выделены одинаковые денежные суммы на приобретение акций двух видов, при этом цена акции вида А составляла 1000 руб., В – 1800 руб. Рассчитаем среднюю цену приобретения акций:

значение варианты с наибольшей частотой.

В дискретных и интервальных рядах

моду определяют по-разному.

Определение моды в дискретных вариационных рядах

Наибольшая частота – 10, Мо = 3.

интервал (интервал с наибольшей частотой), затем ведут расчет по формуле:
,где

– нижняя граница модального интервала,
d – величина интервала,

– частота модального интервала,

– частота интервала, предшествующего модальному,

– частота интервала, следующего за модальным.

упорядоченной по возрастанию значений признака совокупности. Медиана делит вариационный ряд

на две равные части. При этом 50 % единиц совокупности имеют значение меньше медианного, 50 % – больше медианного.

Квартили делят вариационный ряд на четыре равные части: первый квартиль (Q1) показывает значение признака, которого не превышают значения 25 % единиц совокупности, второй квартиль (Q2) – 50 % (он совпадает с медианой), третий (Q3) – 75 %

равных частей: первый дециль показывает значение признака, которого не превышают

значения 10 % единиц совокупности, второй – 20 %, третий – 30 % и т.д. При этом пятый дециль совпадает с медианой и вторым квартилем.

находят ее порядковый номер по формуле:
,где п – объем совокупности,

Номера квартилей:

Номера децилей:

и т.д.

начинает
впервые превышать номер медианы (квартиля, дециля).

медианного интервала,

dMe – величина медианного интервала,

SMe-1 – накопленная частота интервала,

предшествующего медианному,

fMe – частота медианного интервала.

третьего квартиля: