Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЦИЛИНДР И КОНУС
Содержание
- 1. ЦИЛИНДР И КОНУС
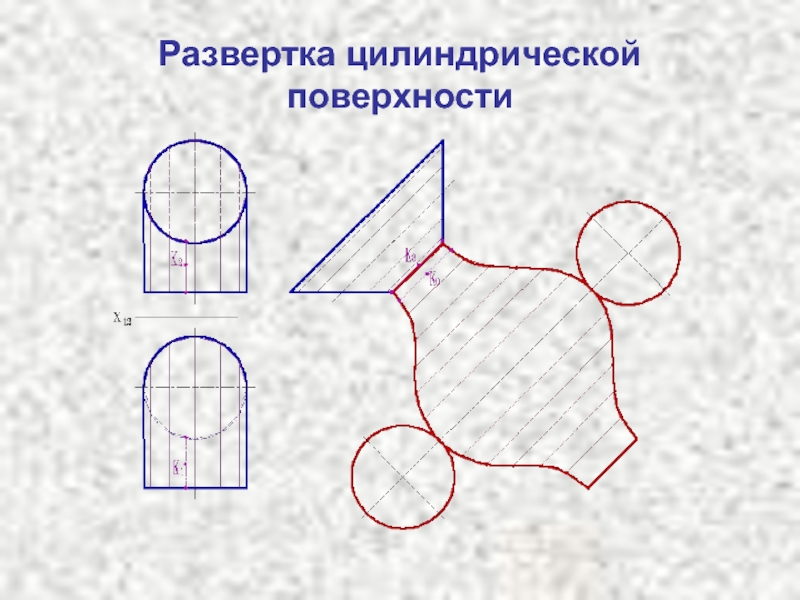
- 2. Развертка цилиндрической поверхности Приближенно развертка цилиндрической поверхности выполняется
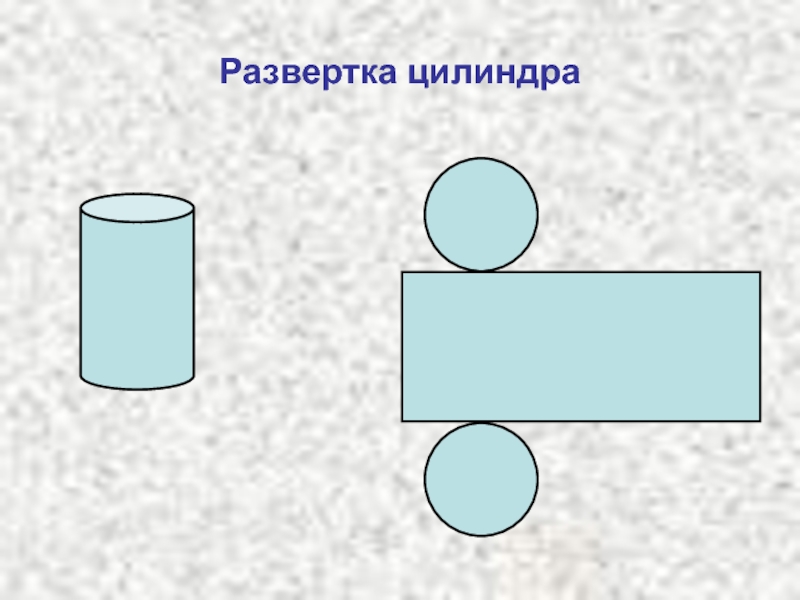
- 3. Развертка цилиндра
- 4. Развертка цилиндрической поверхности
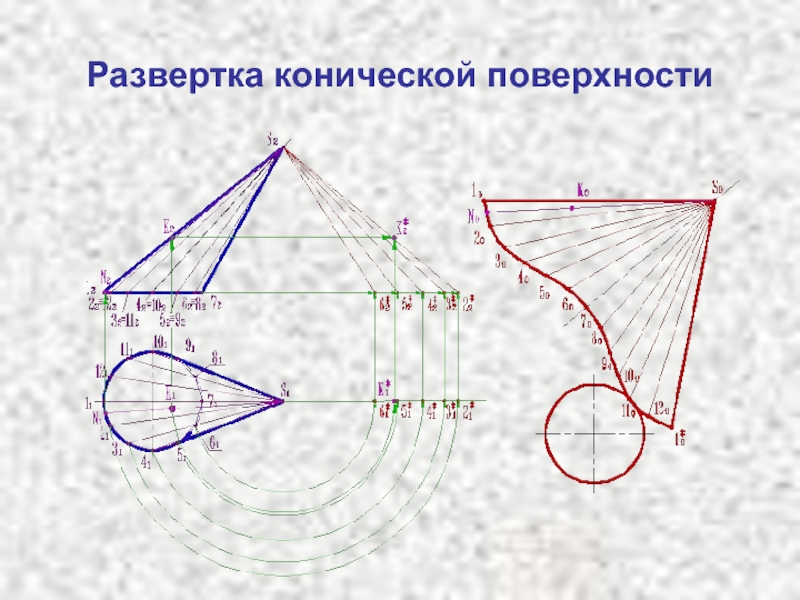
- 5. Развертка конической поверхности вращения Приближенно развертка конической
- 6. Развертка конической поверхности
- 7. Развертка боковой поверхности конуса
- 8. Линии пересечения поверхностей При решении задач на построение
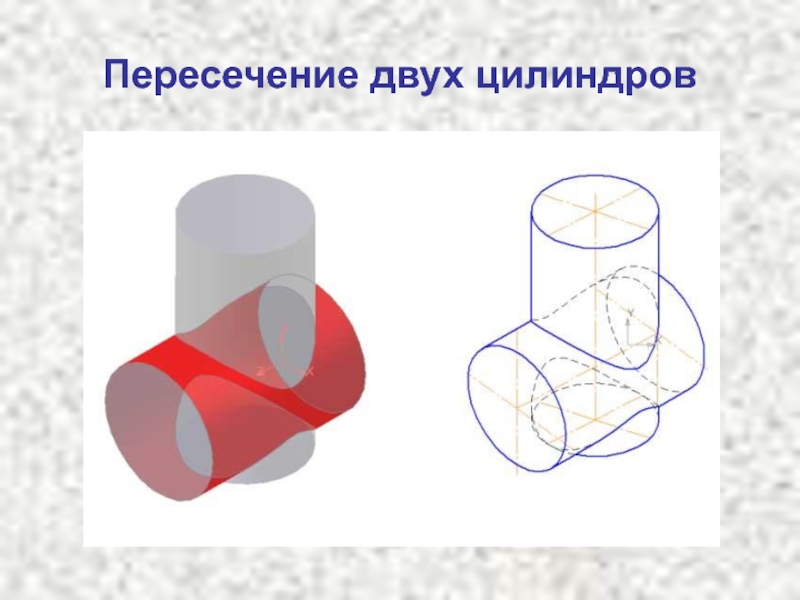
- 9. Пересечение двух цилиндров
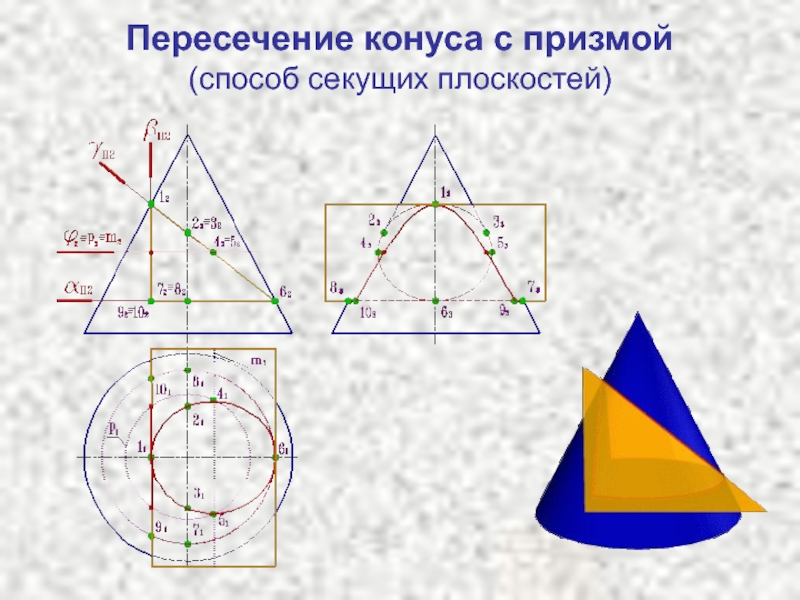
- 10. Пересечение конуса с призмой (способ секущих плоскостей)
- 11. Пересечение поверхностей вращения, оси которых параллельны фронтальной плоскости проекций(способ вспомогательных сфер)
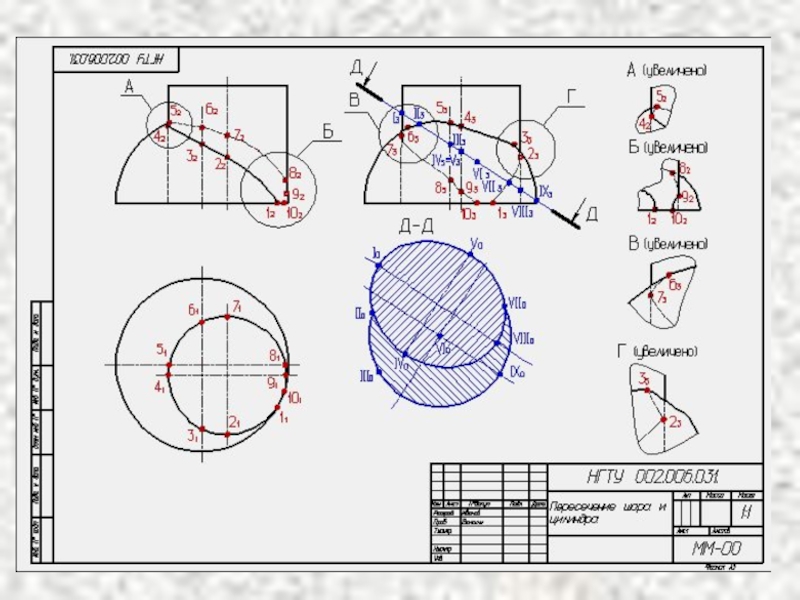
- 12. Пересечение цилиндра и шара
- 13. Слайд 13
- 14. Аксонометрические проекции «Аксонометрия» в переводе с греческого означает
- 15. Вторичной проекцией объекта называется аксонометрическая проекция его проекции на одну из плоскостей на комплексном чертеже.
- 16. Коэффициент искажения – это
- 17. Порядок построения аксонометрии геометрического объекта по его
- 18. Стандартные аксонометрические проекции (ГОСТ 2.317-69) При выполнении чертежей
- 19. Расположение осей в прямоугольной изометрии и диметрии
- 20. Окружность в прямоугольной аксонометрии Окружности,
- 21. y'
- 22. Условности изображения аксонометрии объектов ГОСТ 2.317-69 устанавливает
- 23. Штриховка сечений в аксонометрических проекциях
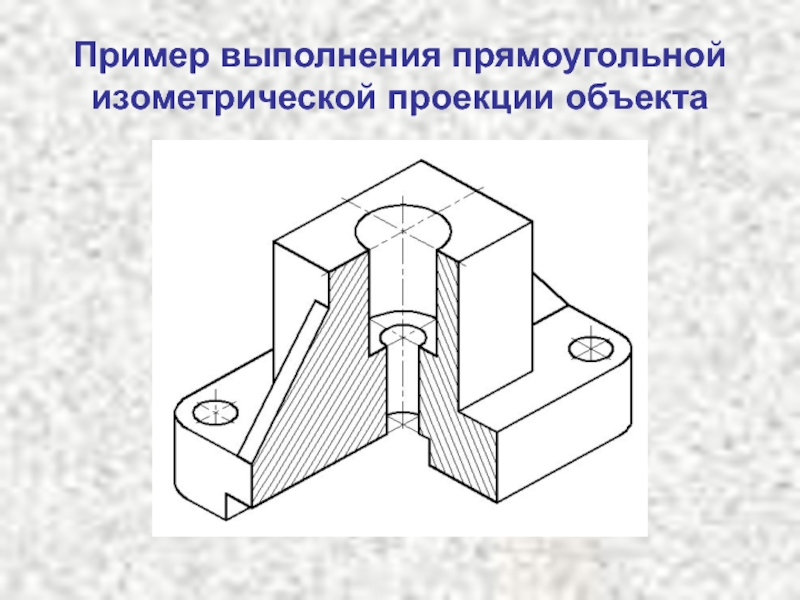
- 24. Пример выполнения прямоугольной изометрической проекции объекта
- 25. Пример выполнения прямоугольной диметрической проекции объекта
- 26. Вопросы для самопроверкиЧто называется разверткой поверхности?Как построить
- 27. Скачать презентанцию
Развертка цилиндрической поверхности Приближенно развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму. Чем больше углов в призме, тем точнее развертка ( при n → ∞ призма
Слайды и текст этой презентации
Слайд 1Лекция №7
Содержание
1. Развертки поверхностей цилиндра и конуса
2. Пересечение многогранника с
поверхностью вращения
Вопросы для самопроверкиСлайд 2Развертка цилиндрической поверхности
Приближенно развертка цилиндрической поверхности выполняется аналогично развертке призмы.
Предварительно в заданный цилиндр вписывают n-угольную призму. Чем больше углов
в призме, тем точнее развертка ( при n → ∞ призма преобразуется в цилиндр).Развертка прямого кругового цилиндра представляет собой прямоугольник, одна сторона которого равна длине образующей l, а вторая – длине окружности основания πd. Для получения полной развертки к боковой поверхности пристраивают два основания.
Слайд 5Развертка конической поверхности вращения
Приближенно развертка конической поверхности выполняется аналогично
развертке пирамиды, предварительно вписав в конус n-угольную пирамиду. Если задана поверхность
прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l,а центральный угол φ=360° r / l,
где r – радиус окружности
основания конуса.
Слайд 8Линии пересечения поверхностей
При решении задач на построение линий пересечения двух
поверхностей в качестве вспомогательной поверхности (посредника) следует выбирать поверхности, которые
пересекали бы заданные поверхности по наиболее простым для построения линиям – прямым или окружностям. Поэтому в качестве поверхностей посредников принимают плоскости или сферы (если оси поверхностей пересекаются, то используют семейство концентрических сфер; если оси не пересекаются, применяют эксцентрические сферы). Чаще всего в качестве вспомогательных плоскостей-посредников используют плоскости уровня. Начинают построения с определения опорных точек линии пересечения.Слайд 11
Пересечение поверхностей вращения, оси которых параллельны фронтальной плоскости проекций
(способ вспомогательных
сфер)
Слайд 14Аксонометрические проекции
«Аксонометрия» в переводе с греческого означает измерение по осям.
Аксонометрической проекцией геометрического объекта называют
его проекцию на аксонометрическую плоскость (картину) вместе с осями координат, с которыми связан проецируемый объект. Аксонометрические чертежи обладают наглядностью и обратимостью, т. е. по аксонометрии и вторичной проекции объекта можно определить все его действительные размеры, и наоборот: по натуральным размерам объекта можно построить его аксонометрию.
Теорема Польке: три отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под произвольными углами к друг другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных осях координат от начала.
Слайд 15
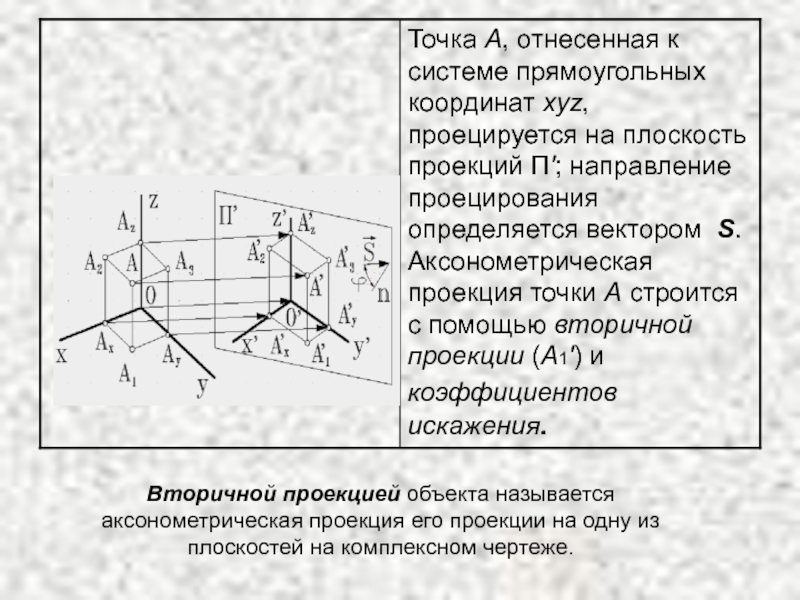
Вторичной проекцией объекта называется аксонометрическая проекция его проекции на одну
из плоскостей на комплексном чертеже.
Слайд 16
Коэффициент искажения – это отношение длины аксонометрической
проекции отрезка к его истинной длине. Для построения аксонометрии объекта
достаточно знать три коэффициента искажения. По оси x' коэффициент искажения составляет u=0'x'/0x, а по осям y' и z' соответственно υ=0'y'/0y и ω=0'z'/0z. В зависимости от коэффициентов искажения аксонометрические проекции могут быть:изометрическими – коэффициенты искажения по всем трем осям равны (u=υ=ω);
диметрическими – коэффициенты искажения по двум любым осям равны между собой, а по третьей – коэффициент искажения отличается от первых двух;
триметрическими, все три коэффициента искажения по осям различны.
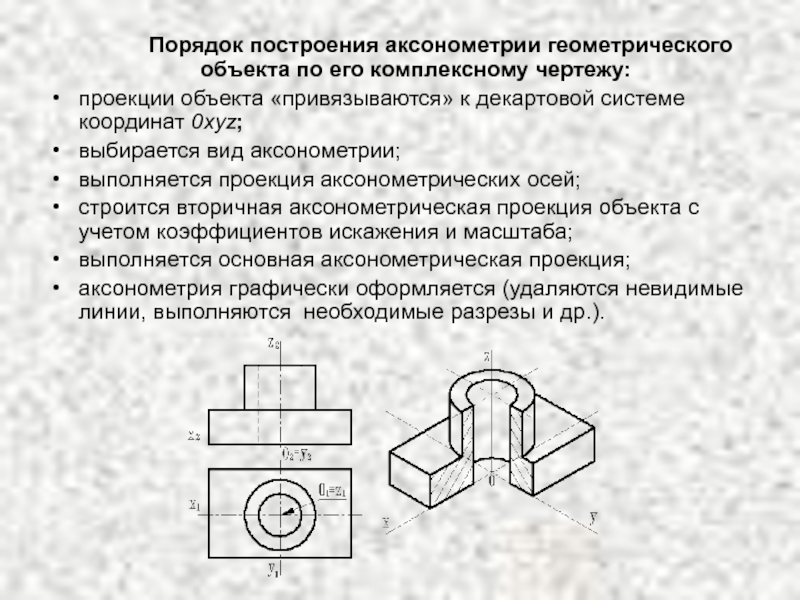
Слайд 17 Порядок построения аксонометрии геометрического объекта по его комплексному чертежу:
проекции
объекта «привязываются» к декартовой системе координат 0xyz;
выбирается вид аксонометрии;
выполняется
проекция аксонометрических осей;строится вторичная аксонометрическая проекция объекта с учетом коэффициентов искажения и масштаба;
выполняется основная аксонометрическая проекция;
аксонометрия графически оформляется (удаляются невидимые линии, выполняются необходимые разрезы и др.).
Слайд 18Стандартные аксонометрические проекции (ГОСТ 2.317-69)
При выполнении чертежей чаще всего используют
прямоугольную и косоугольную (фронтальную и горизонтальную) изометрию, коэффициенты искажения в
которой равны 1:1:1; прямоугольную и косоугольную фронтальную диметрию с коэффициентами искажения 1:0,5:1.В прямоугольной изометрии изображение получается увеличенным относительно оригинала в 1,22 раза за счет того, что размеры не умножаются на коэффициент искажения, а берутся их натуральные величины. Аксонометрические оси располагаются под углом 120°.
Слайд 19Расположение осей в прямоугольной изометрии и диметрии
Расположение аксонометрических осей
прямоугольной
изометрической (а) и прямоугольной диметрической (б)
проекций
а
б
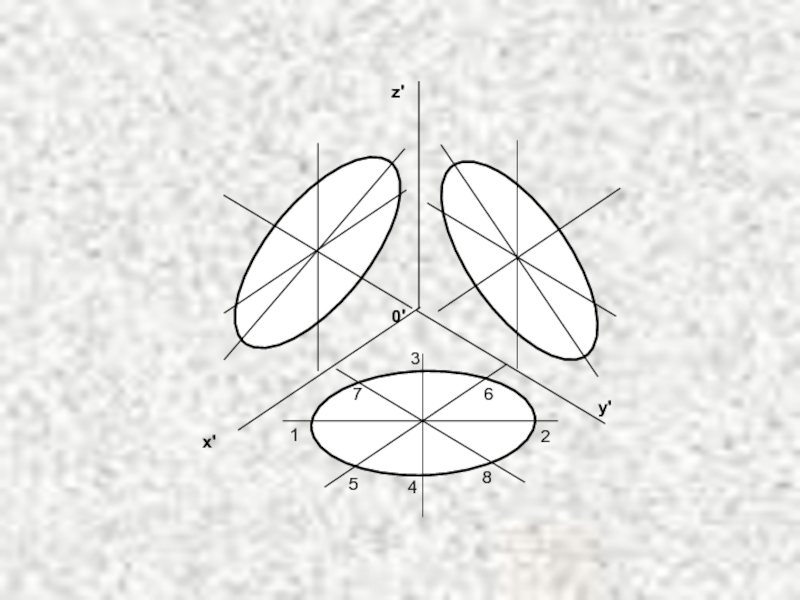
Слайд 20Окружность в прямоугольной аксонометрии
Окружности, лежащие в плоскостях,
параллельных плоскостям проекции, проецируются на аксонометрическую плоскость в виде эллипсов.
ГОСТ 2.317-69 определяет положение окружностей, лежащих в плоскостях, параллельных плоскостям проекций. Для прямоугольной изометрической проекции большая ось эллипса перпендикулярна одной из осей (соответственно 0x, 0y, или 0z) и равна 1,22 диаметра изображаемой окружности; малая ось эллипса равна 0,71 диаметра. Таким образом, найдены четыре точки (1, 2, 3, 4) для построения эллипса, недостающие еще четыре откладывают по линиям, параллельным x, y, z, равные диаметру изображаемой окружности (5–6, 7–8).Слайд 22Условности изображения аксонометрии объектов
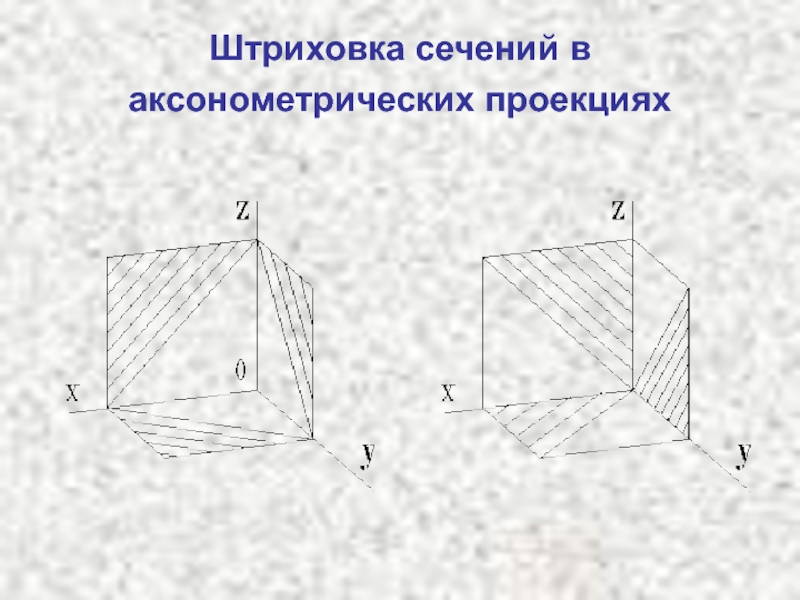
ГОСТ 2.317-69 устанавливает некоторые условности изображения аксонометрии
объектов. Например, линии штриховки сечения в аксонометрических проекциях наносят параллельно
одной из диагоналей проекций квадратов, стороны которых параллельны аксонометрическим осям; тонкостенные элементы: ребра жесткости, спицы маховиков и шкивов штрихуют (в отличие от их изображения на комплексном чертеже).Слайд 26Вопросы для самопроверки
Что называется разверткой поверхности?
Как построить развертку цилиндра?
Как построить
развертку конуса?
Изложите общий принцип построения обобщенного алгоритма для решения задачи
по определению линии пересечения поверхностей.Какие точки называют опорными?
Что называется аксонометрической проекцией?
Перечислить отличия аксонометрических проекций от ортогональных.
Привести алгоритм выполнения аксонометрических изображений объекта.