системе (очень велико)
х – микропараметр, описывающий состояние частицы
х1
Измерения
N1
х2
N2
………..
хi
Ni
1) Пусть х
– дискретная величина вероятность того, что в ходе измерения
получим величину х, равную xi
0 ≤ р(xi) ≤ 1;
- среднее значение х
[1]
[2]


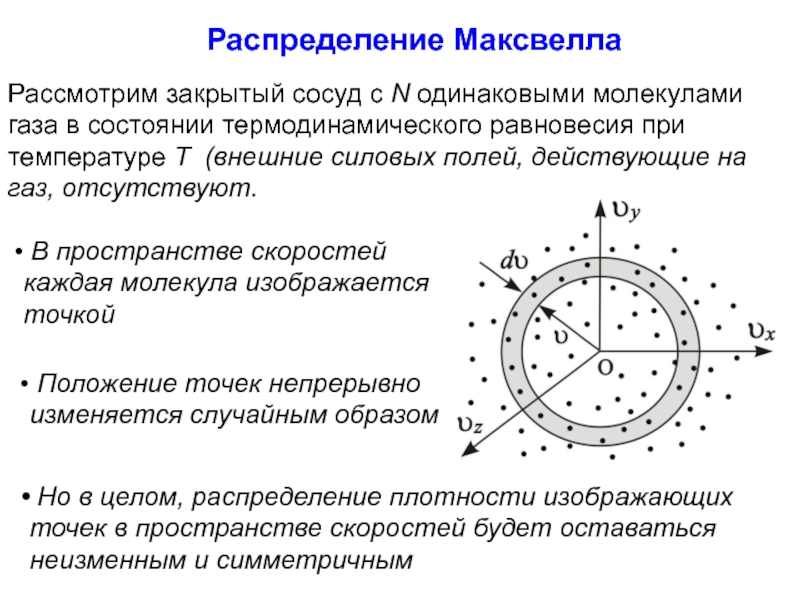

![Статистические распределения Распределение Максвелла 1859 г., Дж. Максвелл: - наиболее вероятная скорость молекул[10][11] Распределение Максвелла 1859 г., Дж. Максвелл: - наиболее вероятная скорость молекул[10][11]](/img/thumbs/924bbd5f8a75b29fa796617f71da727f-800x.jpg)
![Статистические распределения Распределение Максвелла [7][12]- средняя арифметическая скорость молекул[6]среднеквадратичная скорость молекул[13] Распределение Максвелла [7][12]- средняя арифметическая скорость молекул[6]среднеквадратичная скорость молекул[13]](/img/thumbs/560e2c3f76af78a9ee6d7149915c4528-800x.jpg)
![Статистические распределения Распределение Максвелла Зная F(υ), можно найти:(заштрихованная площадь)[9]Влияние температуры и массы молекул на вид графикаυ1υ2 Распределение Максвелла Зная F(υ), можно найти:(заштрихованная площадь)[9]Влияние температуры и массы молекул на вид графикаυ1υ2](/img/thumbs/4dcf8da68ed734b2a6e7b406c6f11a64-800x.jpg)

![Статистические распределения Барометрическая формула:Распределение Больцмана [14] Барометрическая формула:Распределение Больцмана [14]](/img/thumbs/9b74042935e0e9da6129d5b460bba320-800x.jpg)
![Статистические распределения Распределение Больцмана [14], т.к. n ~ P- потенциальная энергия молекулы в Распределение Больцмана [14], т.к. n ~ P- потенциальная энергия молекулы в поле силы тяжестиРаспределение Больцмана позволяет рассчитывать](/img/thumbs/fba6e04aea783ff1f3b16a8f553b7897-800x.jpg)