Слайд 2Нейросетевой подход:
основные положения
Процессы познания -- результат взаимодействия большого
числа простых перерабатывающих элементов, связанных друг с другом и организованных
в слои («модули»). «Переработка информации» -- определенный ответ элемента на воздействия извне.
Знания, управляющие процессом переработки, хранятся в форме весовых коэффициентов связей между элементами сети. Главное -- не элементы, а связи между ними («субсимвольный подход»).
Обучение -- процесс изменения весовых коэффициентов связей между элементами сети (приспособления их к решению определенной задачи).
Слайд 3Классы задач, решаемых современными нейросетями:
Классификация: распознавание образов, распознавание голосов,
верификация подписей, постановка диагноза, анализ экспериментальных данных и т.д.
Моделирование:
поведение системы, поставленной в определенные условия.
Прогноз: погода, ситуация на рынке ценных бумаг, бега, выборы и т.д.
Комплексные задачи:
управление
принятие решений
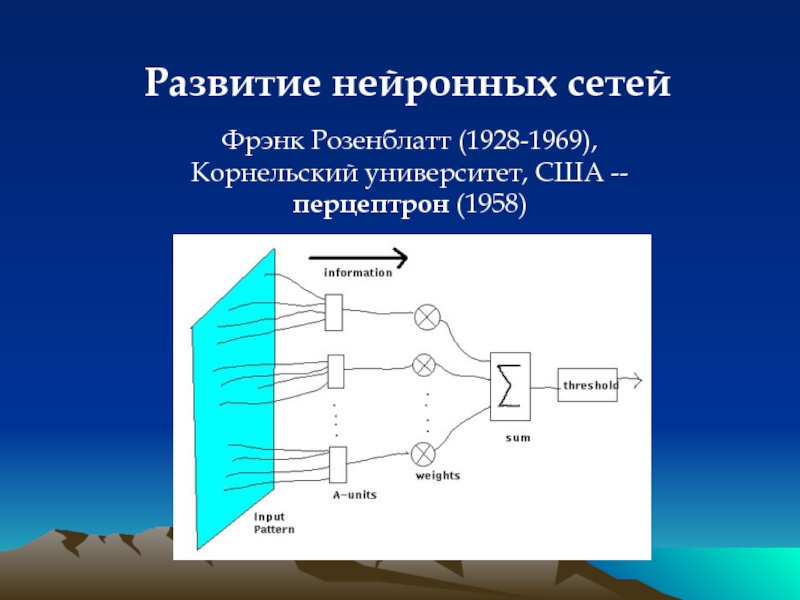
Слайд 4Развитие нейронных сетей
Фрэнк Розенблатт (1928-1969), Корнельский университет, США --
перцептрон (1958)
Слайд 5Развитие нейронных сетей
Фрэнк Розенблатт (1928-1969), Корнельский университет, США
1962 --
«Принципы нейродинамики: перцептроны и теория мозговых механизмов»:
интеграция данных компьютерного
моделирования (включая перцептрон), нейрохирургии, регистрации активности отдельных нейронов и т.д.
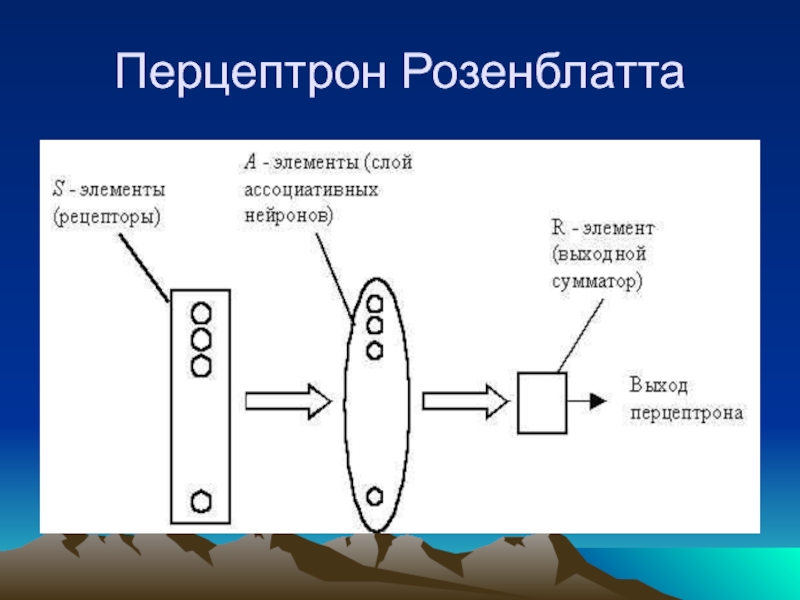
Слайд 7Перцептрон Розенблатта
Однослойный персептрон характеризуется матрицей синаптических связей ||W|| от S-
к A-элементам. Элемент матрицы отвечает связи, ведущей от i-го S-элемента
(строки) к j-му A-элементу (столбцы).
Слайд 8Обучение нейронной сети
Нейронная сеть обучается, чтобы для некоторого множества входных
сигналов давать желаемое множество выходных сигналов. Каждое множество сигналов при
этом рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал требуемый выходной вектор, используя правила, указанные выше.
Слайд 9Обучение перцептрона
Обучение классической нейронной сети состоит в подстройке весовых коэффициентов
каждого нейрона.
Пусть имеется набор пар векторов {xa, ya}, a
= 1..p, называемый обучающей выборкой, состоящей из p объектов.
Вектор {xa} характеризует систему признаков конкретного объекта a обучающей выборки, зафиксированную S-элементами.
Вектор {ya} характеризует картину возбуждения нейронов при предъявлении нейронной сети конкретного объекта a обучающей выборки:
Слайд 11Обучение перцептрона
Будем называть нейронную сеть обученной на данной обучающей выборке,
если при подаче на вход сети вектора {xa} на выходе
всегда получается соответствующий вектор {ya}, т.е. каждому набору признаков соответствуют определенные классы.
Слайд 12Обучение перцепторна
Система связей между рецепторами S и A - элементами,
так же как и пороги A - элементов выбираются некоторым
случайным, но фиксированным образом
Обучение – изменение коэффициентов ki.
Задача: разделять два класса объектов: при предъявлении объектов первого класса выход перцептрона был положителен, а при предъявлении объектов второго класса – отрицательным.
Начальные коэффициенты ki полагаем равными нулю.
Слайд 13Обучение перцептрона
Предъявляем обучающую выборку: объекты (например, круги либо квадраты) с
указанием класса, к которым они принадлежат.
Показываем перцептрону объект первого
класса. При этом некоторые A - элементы возбудятся. Значения возбуждений каждого нейрона образуют входной вектор. Коэффициенты ki , соответствующие этим возбужденным элементам, увеличиваем на 1.
Предъявляем объект второго класса и коэффициенты ki тех A - элементов, которые возбудятся при этом показе, уменьшаем на 1.
Процесс продолжим для всей обучающей выборки. В результате обучения сформируются значения весов связей ki . Значения пороговой функции – выходной вектор.
Слайд 14ОБУЧЕНИЕ НЕЙРОННОЙ СЕТИ
Дональд Олдинг Хебб
(1904-1985)
Итог -- образование «нейронного ансамбля»,
который все быстрее активируется при каждом очередном повторении входа.
Правило
Хебба (1949):
между одновременно активированными нейронами сети пороги синаптической связи снижаются.
Слайд 15Основные понятия:
«Нейрон» (unit, node) -- элемент сети, который суммирует
входные сигналы и, в случае превышения порога его активации, выдает
выходной сигнал (1 или 0) , выполняющий функцию активации или торможения в соответствии с весовым коэффициентом связи между ним и последующими нейронами.
Функция связи между элементами сети («синапса») -- умножение сигнала на весовой коэффициент.
Порог -- весовой коэффициент, связанный с постоянным входным сигналом, равным 1.
Слайд 16Алгоритм обучения (метод градиентного спуска - обратное распространение ошибки)
Выбрать очередную
пару векторов Xk и Yk из обучающей выборки.
Вычислить выход
сети Y .
Вычислить разность между выходом сети Y и требуемым выходным вектором Yk (целевым вектором обучающей пары). Т.е. определить ошибку нейронной сети.
Подкорректировать веса сети wji так, чтобы минимизировать ошибку.
Повторять шаги с 1 по 4 для каждой пары обучающей выборки до тех пор, пока ошибка не достигнет приемлемого уровня.
Слайд 17Обучение нейрона
Угол между векторами: скалярное произведение / произведение длин
Минимизация средней
квадратичной ошибки при помощи корректировки весовых коэффициентов
метод минимальных квадратов
F(x)
= mx+b
MIN SS(m,b) = Σ(yi-f(xi))2 = Σ(yi-mxi-b)2, i=1…n
Слайд 18Нейронные сети
Символьные модели
неявные правила, «интуитивные» задачи (индивидуальные знания): умозаключение
по аналогии, выделение фигуры на фоне и т.п.
явные
правила, формализуемые задачи (культурно-обусловленные общедоступные знания): например, логические и математические задачи.
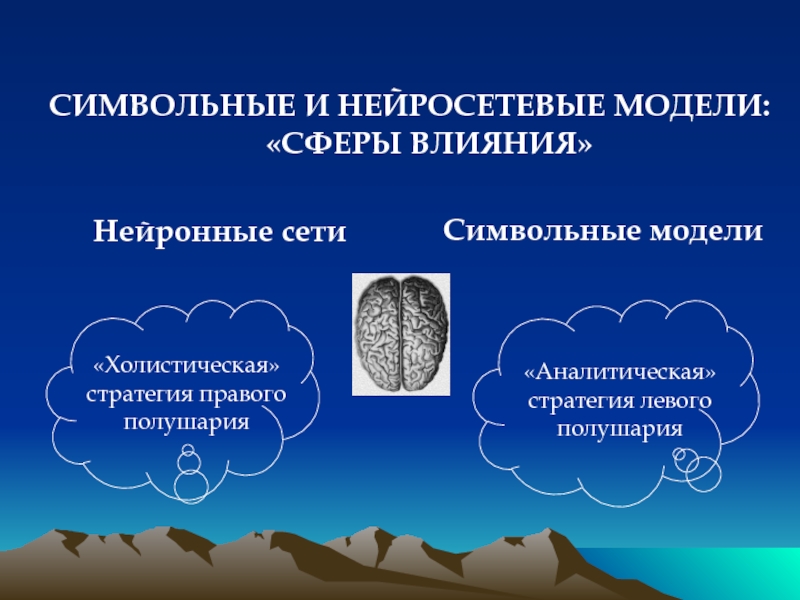
СИМВОЛЬНЫЕ И НЕЙРОСЕТЕВЫЕ МОДЕЛИ: «СФЕРЫ ВЛИЯНИЯ»
Задачи, требующие обучения.
Задачи, требующие конечного набора знаний.
Слайд 19Нейронные сети
Символьные модели
СИМВОЛЬНЫЕ И НЕЙРОСЕТЕВЫЕ МОДЕЛИ: «СФЕРЫ ВЛИЯНИЯ»
Слайд 20 Нейронная сеть
распознавание образов, быстрые ответы на запросы сложной
окружающей среды
ВОЗМОЖНОСТИ ИНТЕГРАЦИИ
НЕЙРОСЕТЕВОГО И СИМВОЛЬНОГО ПОДХОДОВ:
ЭКСПЕРТНЫЕ СИСТЕМЫ
Экспертная
система
принятие решений, логическая проверка выводов с учетом дополнительной информации
Слайд 21ВОЗМОЖНОСТИ ИНТЕГРАЦИИ
НЕЙРОСЕТЕВОГО И МОДУЛЬНОГО ПОДХОДОВ:
ПРОБЛЕМА ВРОЖДЕННОГО И ПРИОБРЕТЕННОГО В ПОЗНАНИИ
«Наследственность»
нейронной сети:
количество элементов
количество слоев
правила и параметры распространения активации и
изменения весов в разных слоях
Достаточно ли этого для развития форм познания, характерных для человека?