Решение линейных неравенств

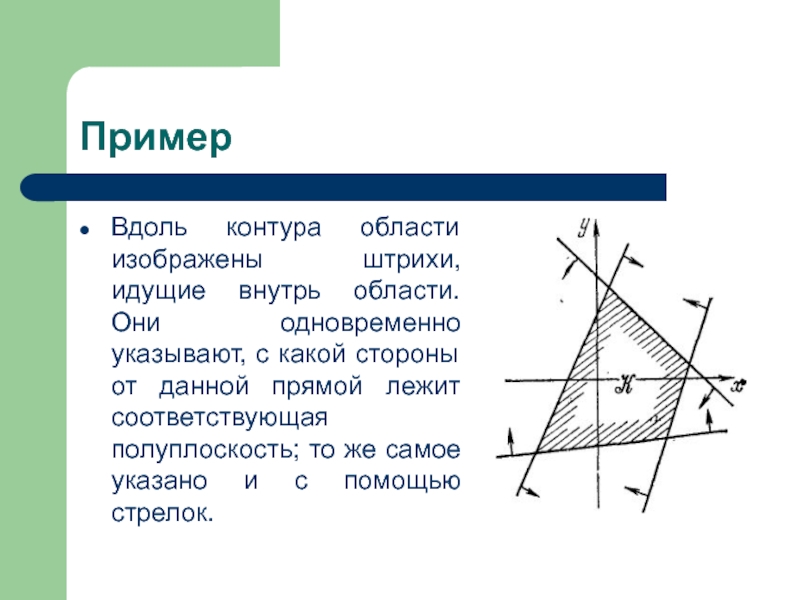
двумя или тремя неизвестными означает задание выпуклой многоугольной области на

плоскости или, соответственно, выпуклого многогранного тела в пространстве.
Начиная с середины 40-х годов этого столетия, возникла новая область прикладной математики – линейное программирование – с важными приложениями в экономике и технике. В конечном счете линейное программирование – это всего лишь один из разделов (хотя и очень важный) теории систем линейных неравенств.

с двумя неизвестными x и y
ax+by+c=0.

(1)
Истолковывая x и y как координаты точки на плоскости, можем сказать, что множество точек, определяемых уравнением (1), есть прямая линия на плоскости.

(2)
Если b≠0, то данное

неравенство приводится к одному из видов у≥kх+p или у≤kх+р.
Первому из этих неравенств удовлетворяют все точки, лежащие «выше» прямой у=kх+р или же на этой прямой, а второму – все точки, лежащие «ниже» прямой у=kх+р или на этой прямой.
Если же b=0, то неравенство приводится к одному из видов х≥h или х≤h. Первому из них удовлетворяют все точки, лежащие «правее» прямой х=h или на этой прямой, второму – все точки, лежащие «левее» прямой х=h или на этой прямой.

неизвестными х и у.
a1x+b1y+c1≥0,
a2x+b2y+c2≥0,
………….........
amx+bmy+cm≥0.

Первое неравенство системы определяет на координатной плоскости

хОу некоторую полуплоскость П1, второе – полуплоскость П2 и т.д. Если пара чисел х, у удовлетворяет всем неравенствам системы, то соответствующая точка М(х, у) принадлежит всем полуплоскостям П1,П2,...,Пm одновременно. Другими словами, точка М принадлежит пересечению (общей части) указанных полуплоскостей. Легко видеть, что пересечение конечного числа полуплоскостей есть некоторая многоугольная область.

указывают, с какой стороны от данной прямой лежит соответствующая полуплоскость;

то же самое указано и с помощью стрелок.

же отметим, что область решений не всегда бывает ограничена; в

результате пересечения нескольких полуплоскостей может возникнуть и неограниченная область.
Имея в виду то обстоятельство, что граница области К состоит из кусков прямых (или из целых прямых), мы говорим, что К есть многоугольная область решений системы.

точки, принадлежащей одновременно всем рассматриваемым полуплоскостям, т.е. когда область К

«пуста»; это означает, что система противоречива.

или в пространстве) называется выпуклым, если вместе с любыми двумя

своими точками А и В оно содержит и весь отрезок АВ.