Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Содержание
- 1. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
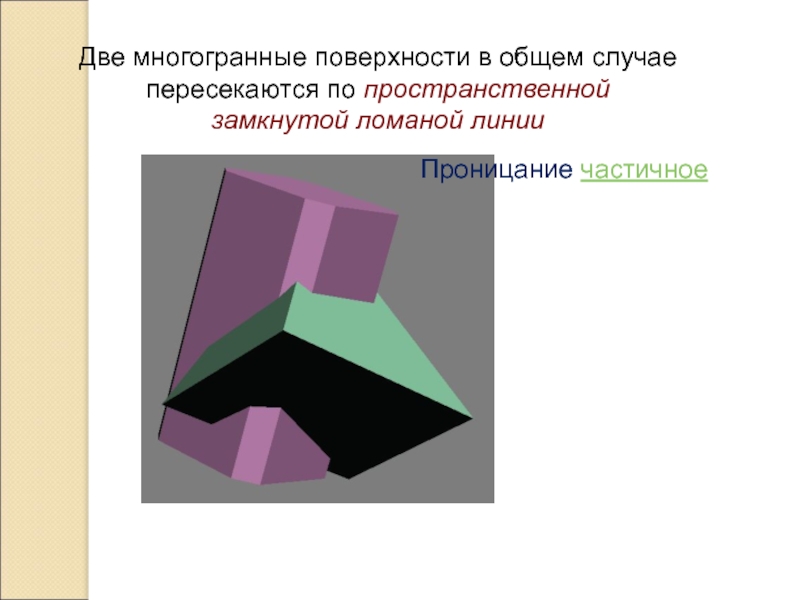
- 2. Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой ломаной линииПроницание частичное
- 3. В частных случаях эта ломаная может распадаться
- 4. Слайд 4
- 5. Перед решением задачи необходимо: 1. Определить форму
- 6. Для определения линии пересечения поверхностей находят ряд
- 7. Общим способом нахождения точек линии пересечения являются
- 8. Когда одна или обе пересекающиеся поверхности проецирующие
- 9. Общее правило построения линии пересечения поверхностей:1. Выбирают
- 10. При построении точек линии пересечения поверхностей в
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
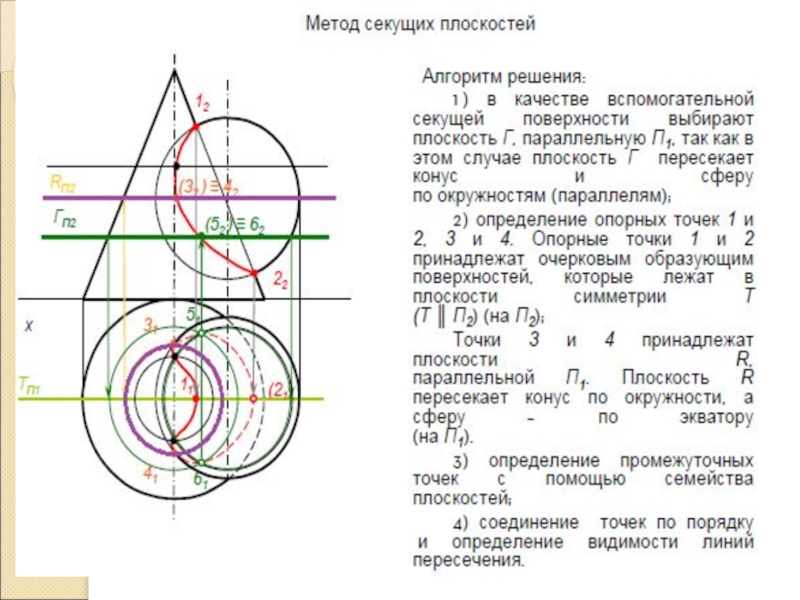
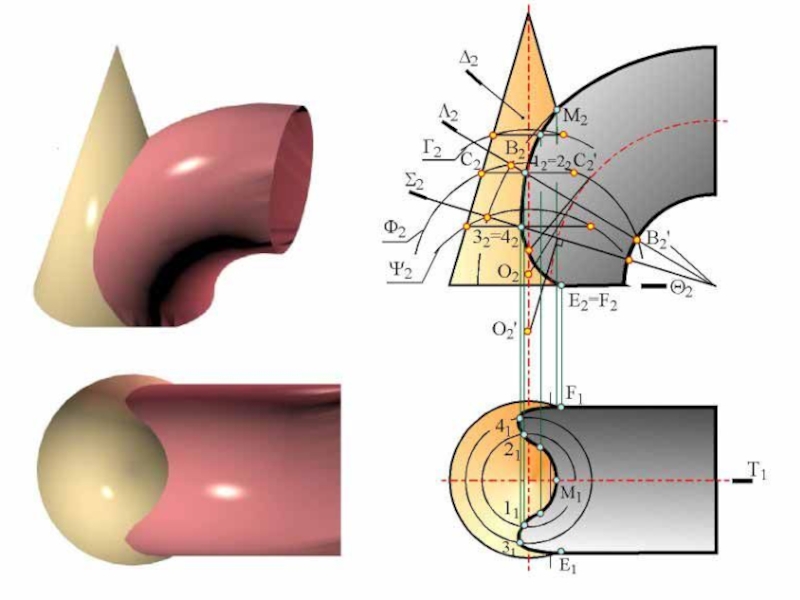
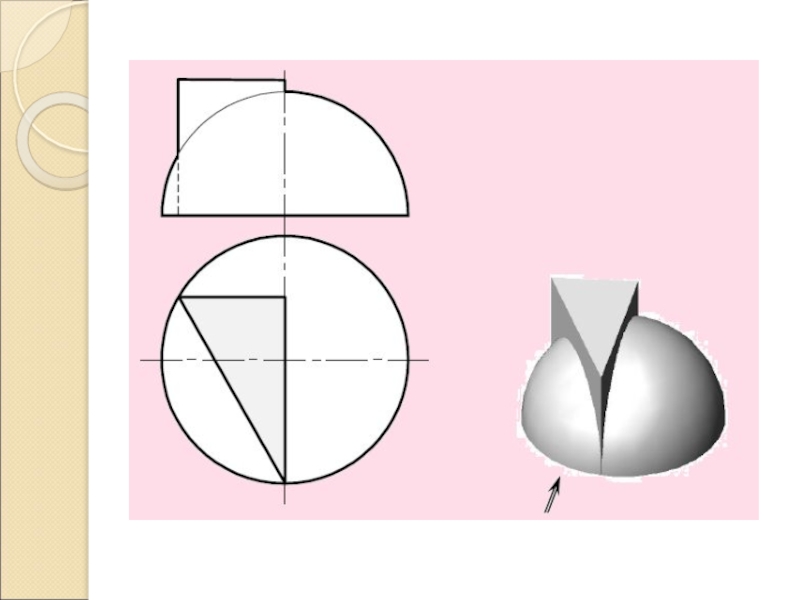
- 15. Пересечение многогранной поверхности с криволинейнойСпособ секущих плоскостей
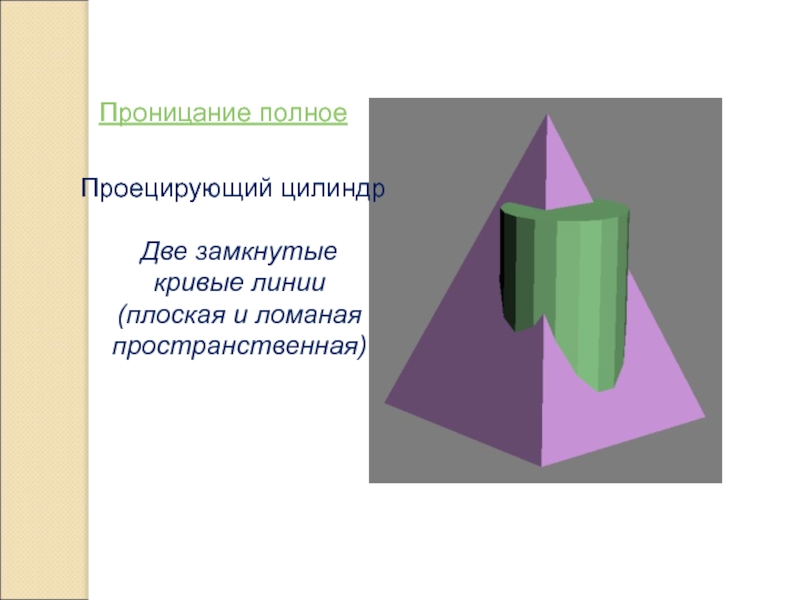
- 16. Проницание полноеДве замкнутые кривые линии (плоская и ломаная пространственная)Проецирующий цилиндр
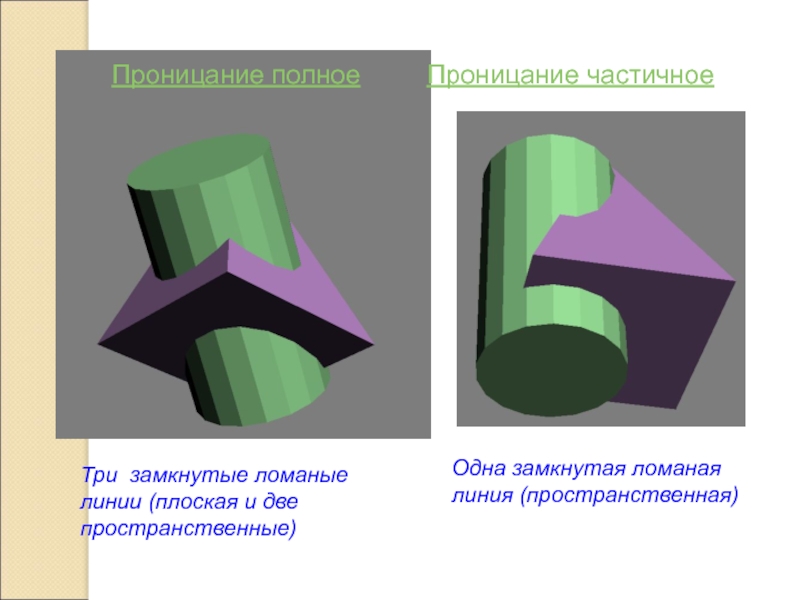
- 17. Проницание полноеТри замкнутые ломаные линии (плоская и две пространственные)Проницание частичноеОдна замкнутая ломаная линия (пространственная)
- 18. S2S1f1t1g1g2t2f2ВТ1 ЗадачаДве замкнутые линии
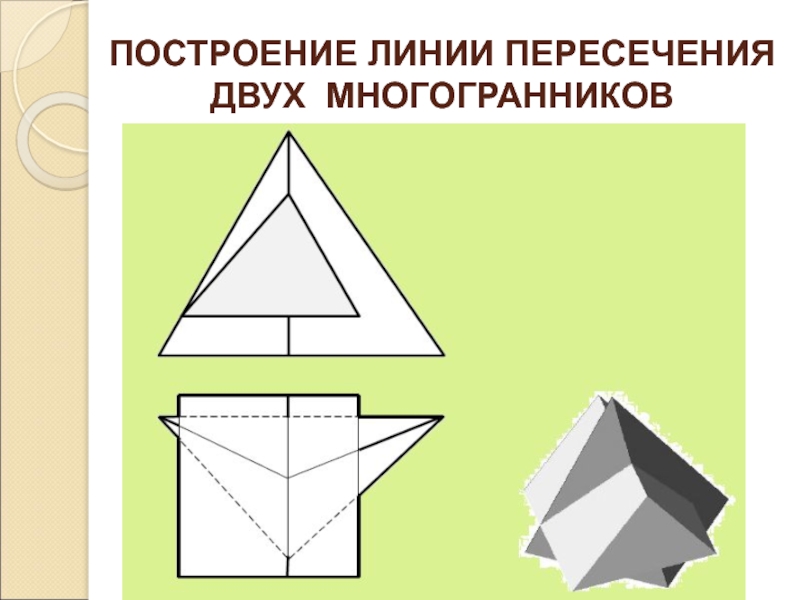
- 19. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ МНОГОГРАННИКОВ
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
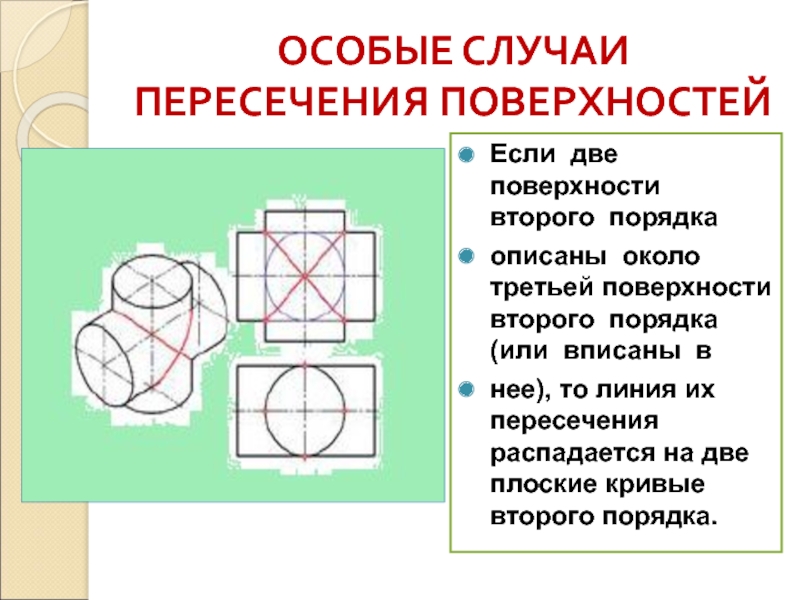
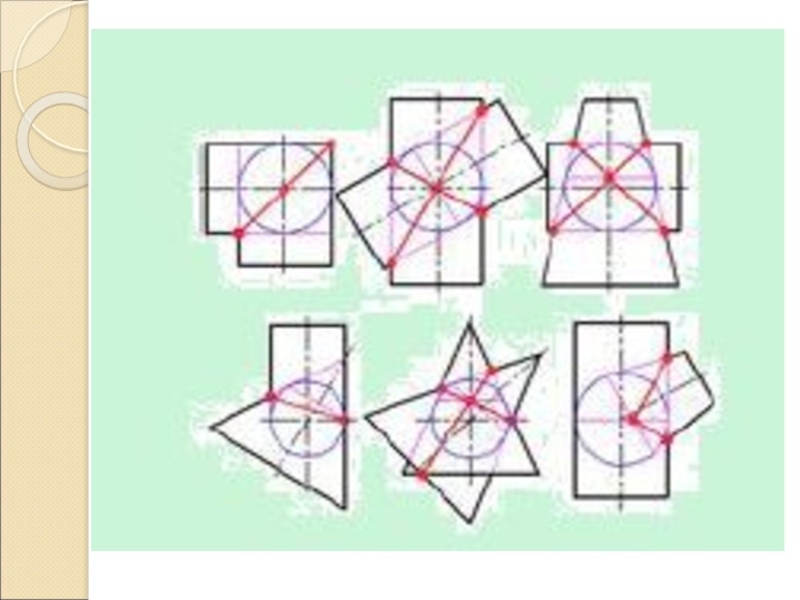
- 23. ОСОБЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙЕсли две поверхности второго
- 24. Слайд 24
- 25. Скачать презентанцию
Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой ломаной линииПроницание частичное
Слайды и текст этой презентации
Слайд 2Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой
ломаной линии
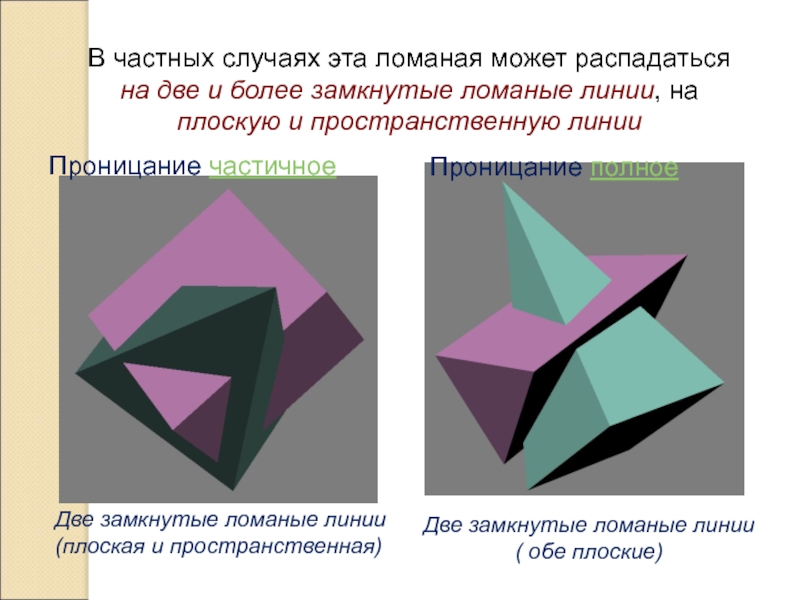
Слайд 3В частных случаях эта ломаная может распадаться на две и
более замкнутые ломаные линии, на плоскую и пространственную линии
Проницание полное
Две
замкнутые ломаные линии (плоская и пространственная)Две замкнутые ломаные линии ( обе плоские)
Проницание частичное
Слайд 4
Линия пересечения распадается
на две отдельные кривые
Полное (проницание) – все образующие одной поверхности
пересекаются со второй поверхностью. Частичное (врезание)– часть образующих одной поверхности пересекается частью образующих другой. Линия пересечения –замкнутая пространственная кривая
Слайд 5
Перед решением задачи необходимо:
1. Определить форму пересекающихся поверхностей.
2. Определить
взаимное расположение поверхностей.
3. Определить расположение этих поверхностей относительно плоскостей проекций.
Слайд 6
Для определения линии пересечения поверхностей находят ряд точек, принадлежащих одновременно
обеим поверхностям, и затем эти точки соединяют в определенной последовательности,
соблюдая видимость.
Слайд 7
Общим способом нахождения точек линии пересечения являются введение вспомогательных секущих
посредников. Вспомогательные секущие посредники выбираются таким образом, чтобы линии, по
которым они пересекают заданные поверхности, получались простыми и удобными для построения (прямые, окружности).
Слайд 8
Когда одна или обе пересекающиеся поверхности проецирующие
(прямая призма, прямой
цилиндр), вводить вспомогательные секущие посредники не требуется, так как уже
имеется одна или две проекции искомой линии пересечения.
Слайд 9Общее правило построения линии пересечения поверхностей:
1. Выбирают вид вспомогательных посредников.
2.
Строят линии пересечения вспомогательных секущих посредников с заданными поверхностями.
3. Находят
точки пересечения построенных линий и соединяют между собой.
Слайд 10При построении точек линии пересечения поверхностей в первую
очередь находят
характерные (опорные) точки – самые высокие и самые низкие точки
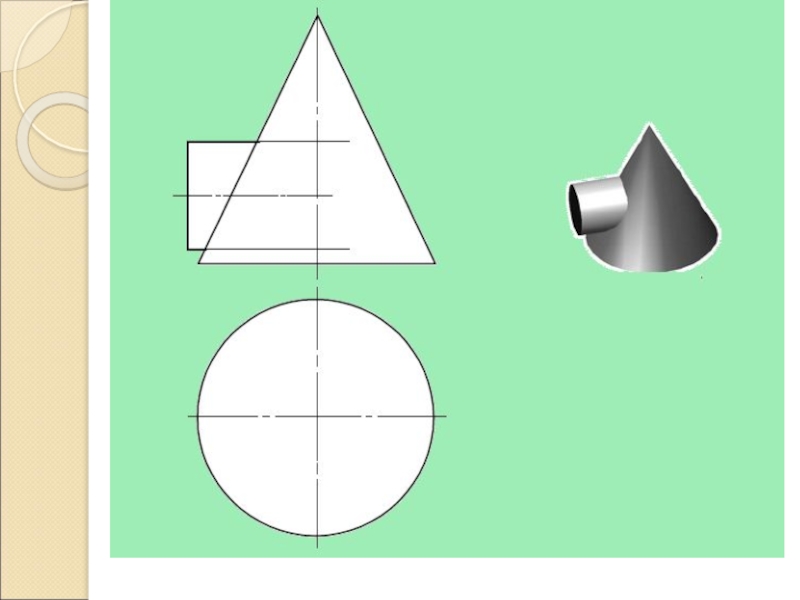
по отношению к плоскости П1; ближайшие и наиболее удаленные по отношению к плоскости П2; точки на очерковых линиях поверхности – точки отделяющие видимую часть проекции линии от невидимой.
Слайд 16Проницание полное
Две замкнутые кривые линии (плоская и ломаная пространственная)
Проецирующий цилиндр
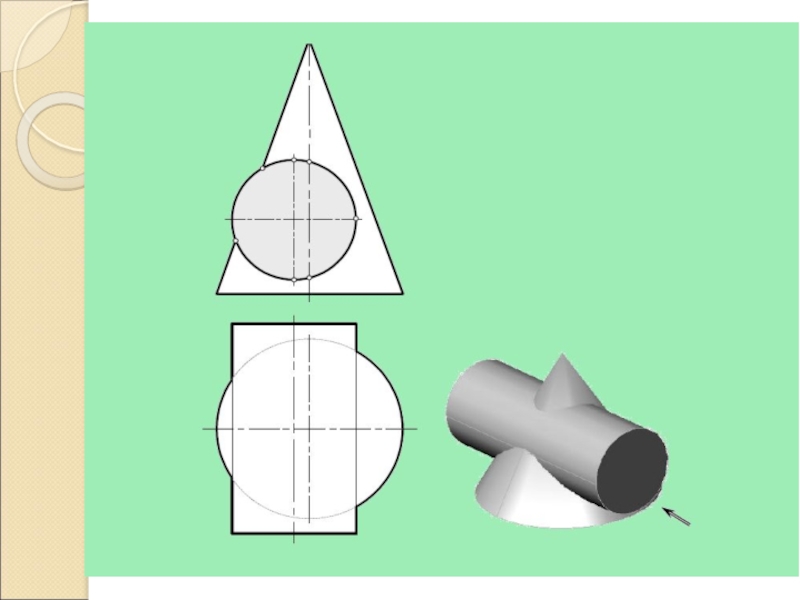
Слайд 17Проницание полное
Три замкнутые ломаные линии (плоская и две пространственные)
Проницание частичное
Одна
замкнутая ломаная линия (пространственная)
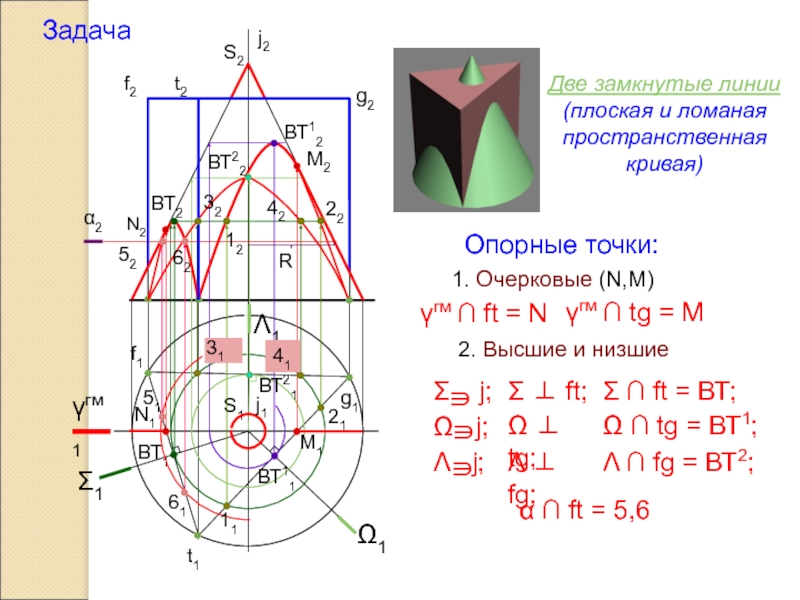
Слайд 18
S2
S1
f1
t1
g1
g2
t2
f2
ВТ1
Задача
Две замкнутые линии (плоская и ломаная
пространственная кривая)
Опорные точки:
2. Высшие и низшие
1. Очерковые (N,M)
γгм1
N1
M1
M2
N2
γгм ∩ ft = N
γгм ∩ tg = M
Σ1
j1
j2
Σ j;
∈
Σ ⊥ ft;
Σ ∩ ft = ВТ;
Ω j;
∈
Ω ⊥ tg;
Ω ∩ tg = ВТ1;
Λ j;
∈
Λ ⊥ fg;
Λ ∩ fg = ВТ2;
Ω1
Λ1
ВТ2
ВТ11
ВТ12
ВТ21
ВТ22
11
21
12
22
31
41
32
42
51
61
52
62
α2
R
α ∩ ft = 5,6
Слайд 23ОСОБЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
Если две поверхности второго порядка
описаны около
третьей поверхности второго порядка (или вписаны в
нее), то линия
их пересечения распадается на две плоские кривые второго порядка.
