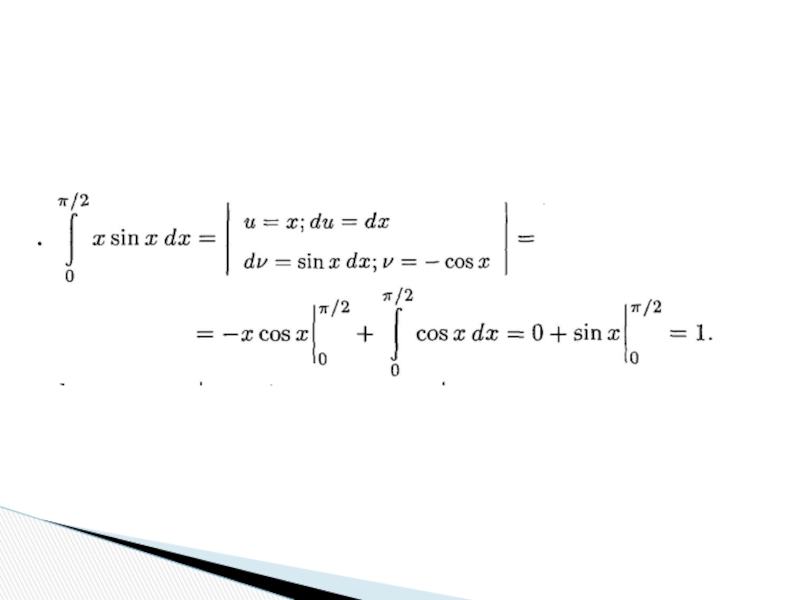Определенный интеграл

Содержание

1. Определенный интеграл
2. Рассмотрим некоторую непрерывную на конечном отрезке [a,b]
3. Слайд 3
4. Из точек деления восставим перпендикуляры к оси
5. На каждом из отрезков [x0, x1], [x1,
6. Составим сумму произведений значений функции y=f (x)
7. или, в сокращенной записи
8. где символ означает суммирование по индексу i , последовательно изменяющемуся от 1 до n включительно.
9. Сумма In называется интегральной суммой функции y=f(x) на отрезке [a,b].
10. Определение: Если существует конечный предел интегральной суммы
11. Слайд 11
12. Процесс вычисления определенного интеграла называется интегрированием.Функция f(x)
13. Если функция f(x) непрерывна в замкнутом интервале
14. Основное отличие определенного интеграла от неопределенного:Неопределенный интеграл – это семейство первообразных функций;Определенный интеграл – число!
15. Определенный интеграл равен площади криволинейной трапеции, т.е.
16. Слайд 16
17. Слайд 17
18. 2. Свойства определенного интеграла
19. Слайд 19
20. Слайд 20
21. Слайд 21
22. Слайд 22
23. Слайд 23
24. 3. Формула Ньютона-Лейбница
25. Слайд 25
26. а) Метод разложения (непосредственного интегрирования)4. Основные методы вычисления определенных интегралов.
27. б) Метод замены переменной (подстановки)
28. в) Метод интегрирования по частям
29. Слайд 29
30. Физический смысл определенного интеграла – работа переменной силы.5. Физический смысл определенного интеграла
31. Скачать презентанцию

Рассмотрим некоторую непрерывную на конечном отрезке [a,b] функцию y=f(x).Разделим отрезок [a,b] на n частей (необязательно равных) и обозначим абсциссы точек деления A0, A1, A2, …, An-2, An-1, An в порядке возрастания

Главная
Разное
Определенный интеграл

Слайды и текст этой презентации

Слайд 1ЛЕКЦИЯ № 4

по дисциплине «Математика»
на тему: «Определенный интеграл»

для курсантов I

курса по военной специальности «Фармация»

ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ имени С.М. Кирова Кафедра биологической и

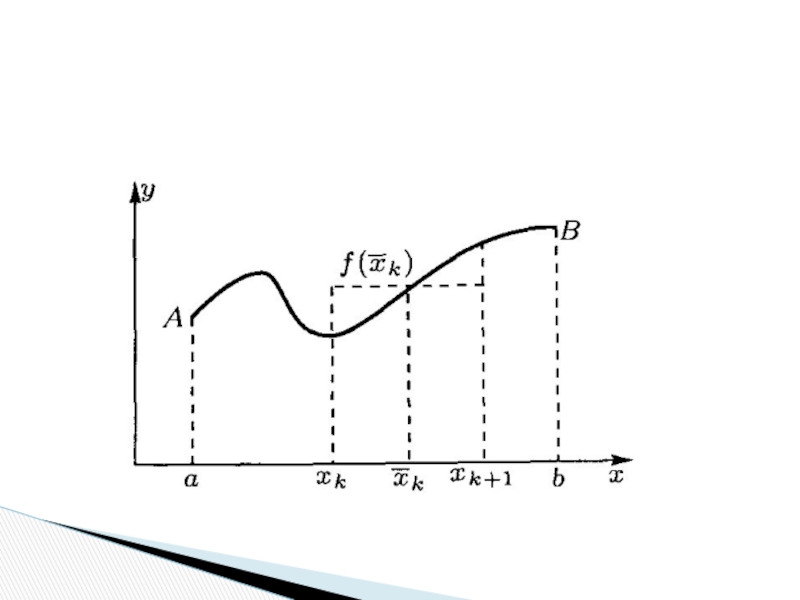
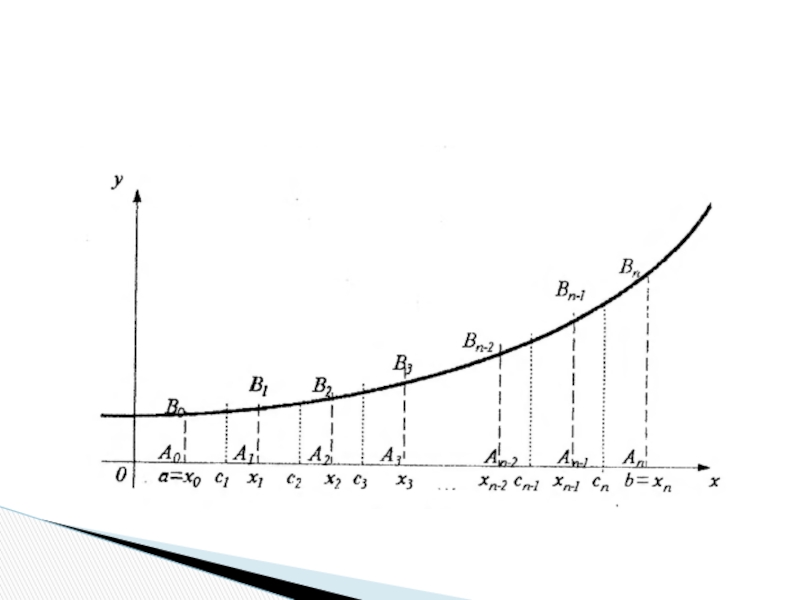
медицинской физики

ЛЕКЦИЯ № 4по дисциплине «Математика»на тему: «Определенный интеграл» для курсантов I курса по военной специальности «Фармация»ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ имени

Слайд 2Рассмотрим некоторую непрерывную на конечном отрезке [a,b] функцию y=f(x).
Разделим отрезок

[a,b] на n частей (необязательно равных) и обозначим абсциссы точек

деления A0, A1, A2, …, An-2, An-1, An в порядке возрастания следующим образом:
x0=a, x1, x2, x3, …, xn-2, xn-1, xn=b

1. Определенный интеграл. Теорема существования.

Рассмотрим некоторую непрерывную на конечном отрезке [a,b] функцию y=f(x).Разделим отрезок [a,b] на n частей (необязательно равных) и

Слайд 3

Слайд 4

Из точек деления восставим перпендикуляры к оси абсцисс до их

пересечения с графиком функции в точках, соответственно:
B0, B1, B2, …,

Bn-2, Bn-1, Bn

Из точек деления восставим перпендикуляры к оси абсцисс до их пересечения с графиком функции в точках, соответственно:B0,

Слайд 5
На каждом из отрезков [x0, x1], [x1, x2], [x2, x3],

…, [xn-2, xn-1], [xn-1, xn] (эти отрезки в отличие от

всего отрезка [a,b] называют частичными отрезками) выберем по одной точке (необязательно в центре отрезка), обозначив их, соответственно, с1, с2, с3, …, сn-2, сn-1, сn.
Из этих точек также восставим перпендикуляры к оси абсцисс до их пересечения с графиком функции.

На каждом из отрезков [x0, x1], [x1, x2], [x2, x3], …, [xn-2, xn-1], [xn-1, xn] (эти отрезки

Слайд 6Составим сумму произведений значений функции y=f (x) в точках ci

, где индекс i – номер частичного отрезка (1, 2,

3, …, n), на величины Δxi=xi-xi-1 соответствующих отрезков:

Составим сумму произведений значений функции y=f (x) в точках ci , где индекс i – номер частичного

Слайд 7

или, в сокращенной записи

Слайд 8
где символ

означает суммирование по индексу i , последовательно изменяющемуся от

1 до n включительно.

Слайд 9

Сумма In называется интегральной суммой функции y=f(x) на отрезке [a,b].

Слайд 10Определение: Если существует конечный предел интегральной суммы функции y=f(x) на

отрезке [a,b] при стремлении к 0 величины максимального из частичных

отрезков, не зависящий от способа разделения данного отрезка на частичные отрезки и выбора на них точек ci , то такой предел называют определенным интегралом от этой функции на данном отрезке и обозначают следующим образом:

Определение: Если существует конечный предел интегральной суммы функции y=f(x) на отрезке [a,b] при стремлении к 0 величины

Слайд 11

Слайд 12
Процесс вычисления определенного интеграла называется интегрированием.
Функция f(x) – подынтегральная функция,
x

– переменная интегрирования.
Числа a и b (границы отрезка [a,b]) называют,

соответственно, нижним и верхним пределами интегрирования.

Процесс вычисления определенного интеграла называется интегрированием.Функция f(x) – подынтегральная функция,x – переменная интегрирования.Числа a и b (границы

Слайд 13Если функция f(x) непрерывна в замкнутом интервале [a,b], то ее

n-ная интегральная сумма стремится к пределу при стремлении к нулю

наибольшего частичного интервала. Этот предел не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.

Теорема существования определенного интеграла:

Если функция f(x) непрерывна в замкнутом интервале [a,b], то ее n-ная интегральная сумма стремится к пределу при

Слайд 14Основное отличие определенного интеграла от неопределенного:
Неопределенный интеграл – это семейство

первообразных функций;
Определенный интеграл – число!

Основное отличие определенного интеграла от неопределенного:Неопределенный интеграл – это семейство первообразных функций;Определенный интеграл – число!

Слайд 15
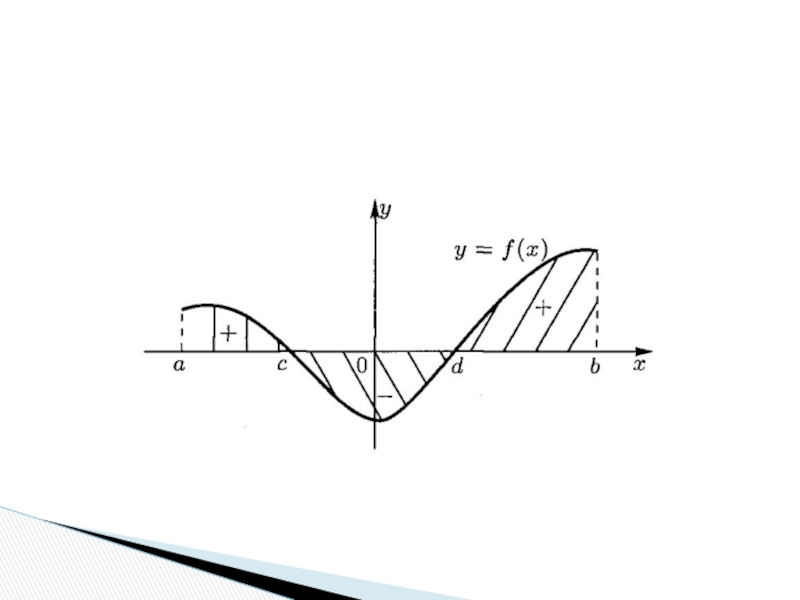
Определенный интеграл равен площади криволинейной трапеции, т.е. плоской фигуры, ограниченной

сверху графиком непрерывной функции у= f(x) , снизу – осью

абсцисс, слева – прямой линией x=a, справа – прямой линией x=b.

Геометрический смысл определенного интеграла:

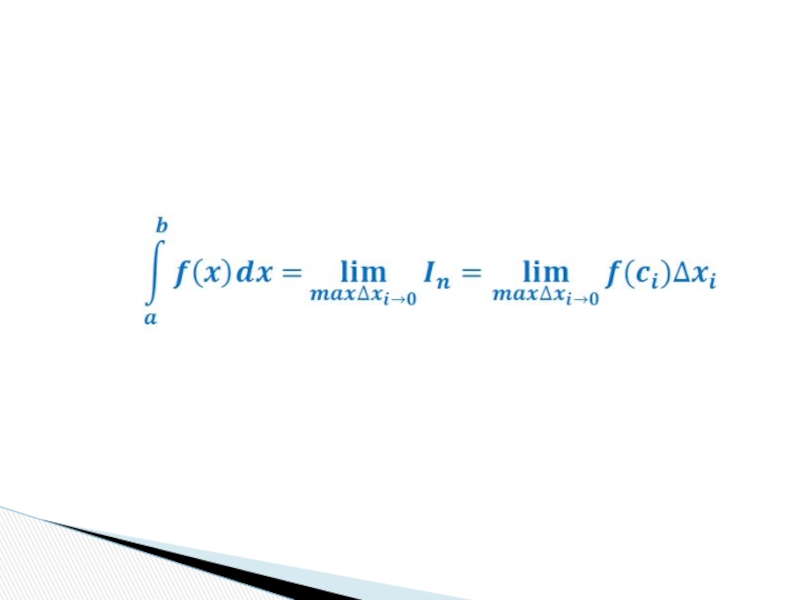
Определенный интеграл равен площади криволинейной трапеции, т.е. плоской фигуры, ограниченной сверху графиком непрерывной функции у= f(x) ,

Слайд 16

Слайд 17

Слайд 182. Свойства определенного интеграла

Слайд 243. Формула Ньютона-Лейбница

Слайд 25

Слайд 26а) Метод разложения (непосредственного интегрирования)

4. Основные методы вычисления определенных интегралов.

Слайд 27б) Метод замены переменной (подстановки)

Слайд 28в) Метод интегрирования по частям

Слайд 29

Слайд 30

Физический смысл определенного интеграла – работа переменной силы.

5. Физический смысл

определенного интеграла

Скачать презентацию

Разделы презентаций

Определенный интеграл

Содержание

Слайды и текст этой презентации

Слайд 1ЛЕКЦИЯ № 4по дисциплине «Математика»на тему: «Определенный интеграл» для курсантов I

курса по военной специальности «Фармация»ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ имени С.М. Кирова Кафедра биологической и

Слайд 2Рассмотрим некоторую непрерывную на конечном отрезке [a,b] функцию y=f(x).Разделим отрезок

[a,b] на n частей (необязательно равных) и обозначим абсциссы точек

Слайд 4Из точек деления восставим перпендикуляры к оси абсцисс до их

пересечения с графиком функции в точках, соответственно:B0, B1, B2, …,

Слайд 5На каждом из отрезков [x0, x1], [x1, x2], [x2, x3],

…, [xn-2, xn-1], [xn-1, xn] (эти отрезки в отличие от

Слайд 6Составим сумму произведений значений функции y=f (x) в точках ci

, где индекс i – номер частичного отрезка (1, 2,

Слайд 7или, в сокращенной записи

Слайд 8где символ означает суммирование по индексу i , последовательно изменяющемуся от