Логические основы ЭВМ

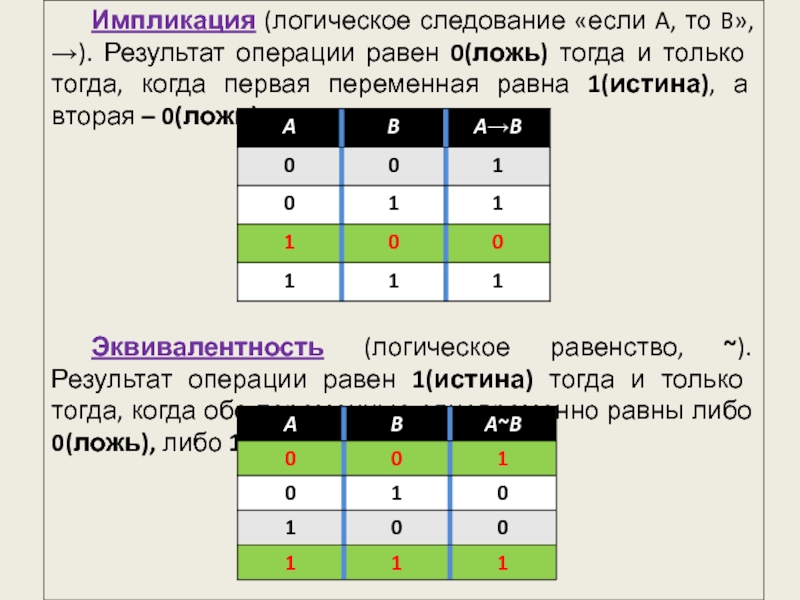
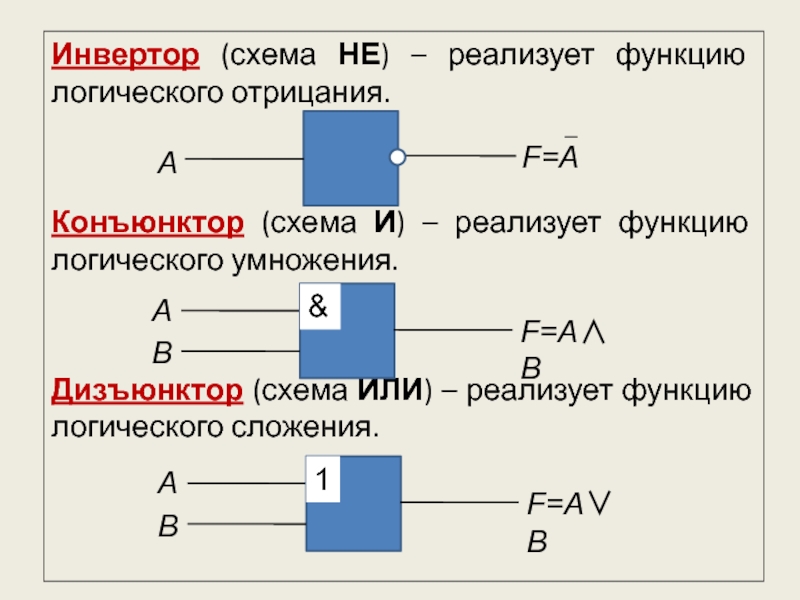
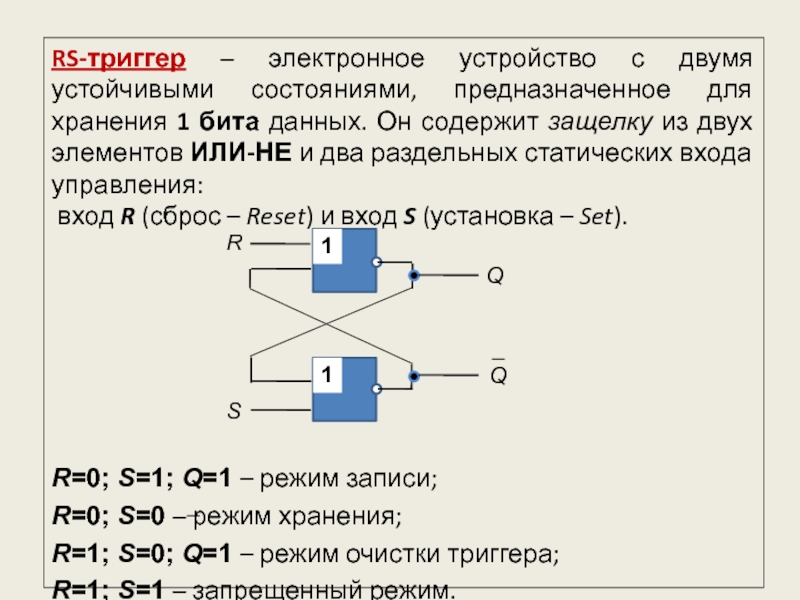
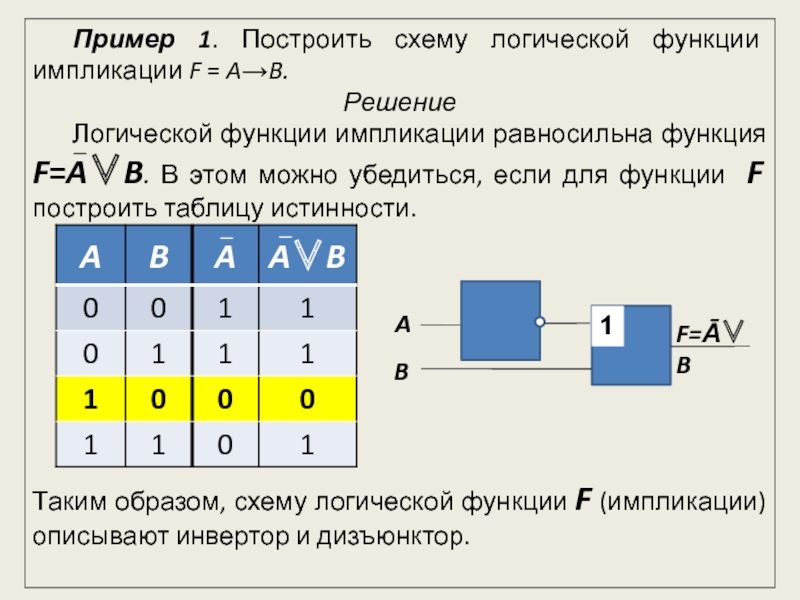
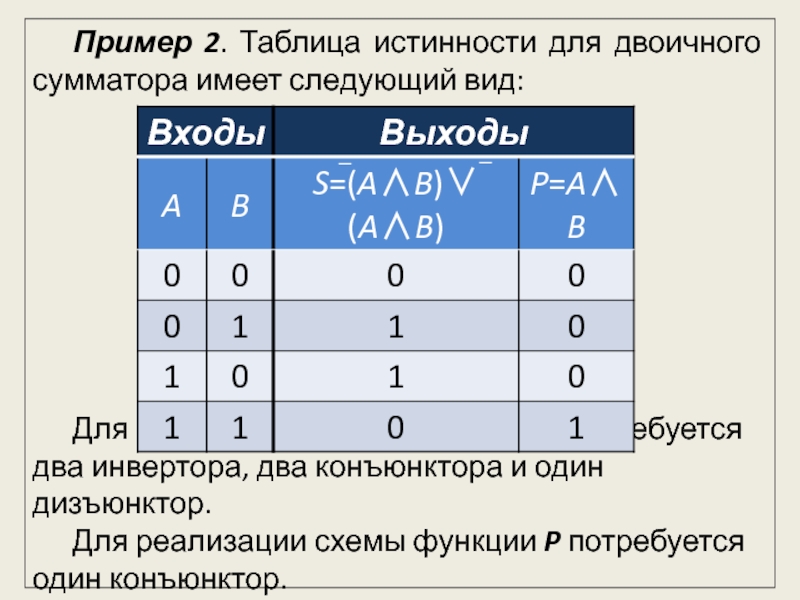
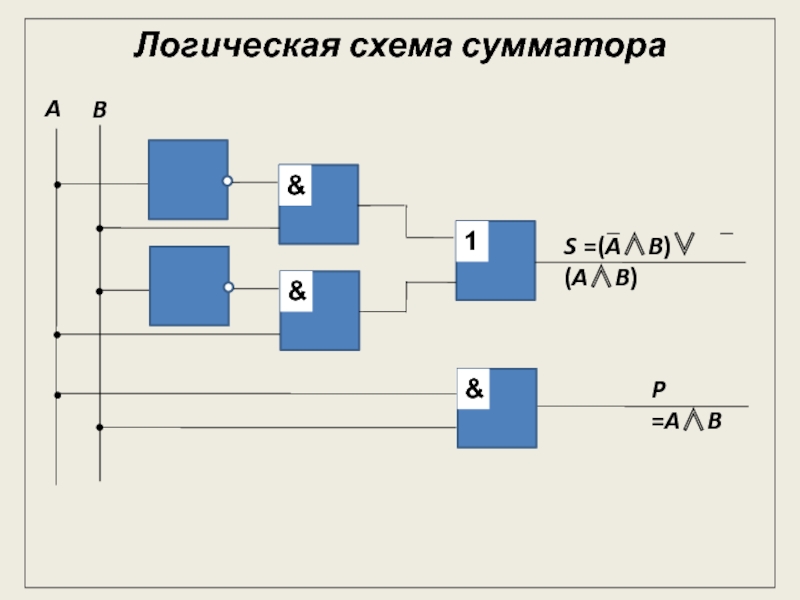
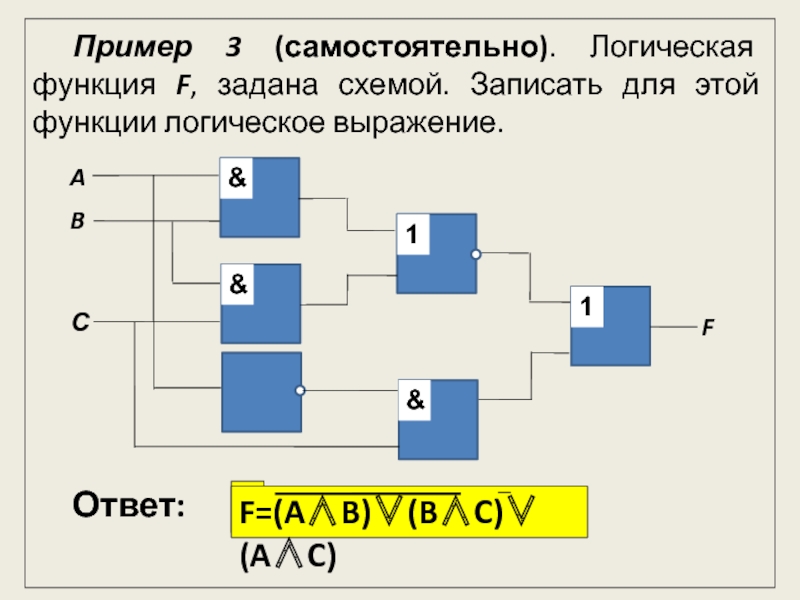
представляет собой электронную схему, состоящую из простых логических элементов, работа

которых базируется на законах и правилах алгебры логики.
Алгебра логики (булева алгебра) – раздел дискретной математики, изучающий высказывания и логические операции над ними.
Высказывание – связное повествовательное предложение, о котором можно сказать, истинно оно или ложно.

значения (Истина или Ложь), логические переменные, логические функции и логические

операции.
Логические операции
В алгебре логики имеются три базовые операции:
логическое отрицание (инверсия, НЕ, NOT, ¬, ⎯);
логическое умножение (конъюнкция, И, AND, &, ∧);
логическое сложение (дизъюнкция, ИЛИ, OR, |, ∨, +).
Другие логические операции путем логических преобразований могут быть сведены к трем базовым операциям.

сочетания логических значений операндов вместе со значением результата операции для

каждого из этих сочетаний.
Инверсия. Результат операции логического отрицания равен 1(истина), если значение переменной равно 0(ложь) и, наоборот, результат равен 0(ложь), если переменная равна 1(истина).

равны 1(истина).





Дизъюнкция. Результат операции равен 0(ложь) только тогда, когда обе

переменные равны 0(ложь).

равен 0(ложь) тогда и только тогда, когда первая переменная равна

1(истина), а вторая – 0(ложь).




Эквивалентность (логическое равенство, ~). Результат операции равен 1(истина) тогда и только тогда, когда обе переменные одновременно равны либо 0(ложь), либо 1(истина).

формул следующие:
1) инверсия;
2) конъюнкция;
3) дизъюнкция;
4) импликация;

5) эквивалентность.

Для преобразования логических формул с целью их упрощения используются законы алгебры логики.

= B∧A;
ассоциативные (сочетательные):
A∨(B∨C) = (A∨B) ∨C; A∧(B∧C) = (A∧B) ∧C;

отрицание:
A∨A = 1; A∧A= 0; A = A;
двойственность (правило де Моргана):
A∨B = A ∧ B; A∧B = A∨B;
дистрибутивные (распределительные):
A∨(B∧C) = (A∨B) ∧ (A∨C); A∧(B∨C) = (A∧B) ∨(A∧C);
поглощение:
A∨(A∧B) = A ; A∧(A∨B) = A.

=

_

_

_

_

_

_

∧ B = (A∧A)∧(B∧B) = 0


(A∧B) ∨A∨B ∨A =

(A∧B) ∨(A∧B) ∨A = = A∧(B∨B) ∨A = (A∧1)∨A = A∨A = 1

A∧B ∨B ∨C = A∨B∨(B ∧C) = A∨B∨(B ∧C) = = A∨B

_

_

_

_

_

_

_

0

B

_

∧

_

_

_

_

_

_

1

_

_

_

_

_

_

_

_

_

_

_

_

_

B

_

A

_

A∧B∨(A∧B)
Указать, при каких значениях переменных A и B логическая

функция F = 0?







Ответ: логическая функция F = 0 при A = 1 и B = 1.

_

_

_

_

элементарную логическую функцию.
На входы логического элемента поступают сигналы – значения

аргументов, на выходе появляется сигнал – значение функции. Входные и выходные сигналы логических элементов могут иметь одно из двух логических состояний: 1 (истина) или 0 (ложь).
К базовым логическим элементам относятся электронные схемы: НЕ, И, ИЛИ, И–НЕ, ИЛИ–НЕ, а также триггер.

– реализует функцию логического умножения.


Дизъюнктор (схема ИЛИ) – реализует функцию

логического сложения.

F=A

_

F=A∧B

B

A

&

A

F=A∨B

B

A

1

ИЛИ-НЕ – реализует функцию логического отрицания результата схемы ИЛИ.




F=A∨B
B
A
1

F=A∧B
B
A
&

хранения 1 бита данных. Он содержит защелку из двух элементов

ИЛИ-НЕ и два раздельных статических входа управления: вход R (сброс – Reset) и вход S (установка – Set).






R=0; S=1; Q=1 – режим записи;
R=0; S=0 – режим хранения;
R=1; S=0; Q=1 – режим очистки триггера;
R=1; S=1 – запрещенный режим.

Q

S

R

1

Q

1

_

_

функции импликации равносильна функция F=A∨B. В этом можно убедиться, если

для функции F построить таблицу истинности.








Таким образом, схему логической функции F (импликации) описывают инвертор и дизъюнктор.

_

_

_

1

A

B

F=Ā∨B

реализации схемы функции S потребуется два инвертора, два конъюнктора и

один дизъюнктор.
Для реализации схемы функции P потребуется один конъюнктор.

_

_

этой функции логическое выражение.










Ответ:


&
A
B



&

1

&

1
С
F
?
F=(A∧B)∨(B∧C)∨(A∧C)
_