Матрицы

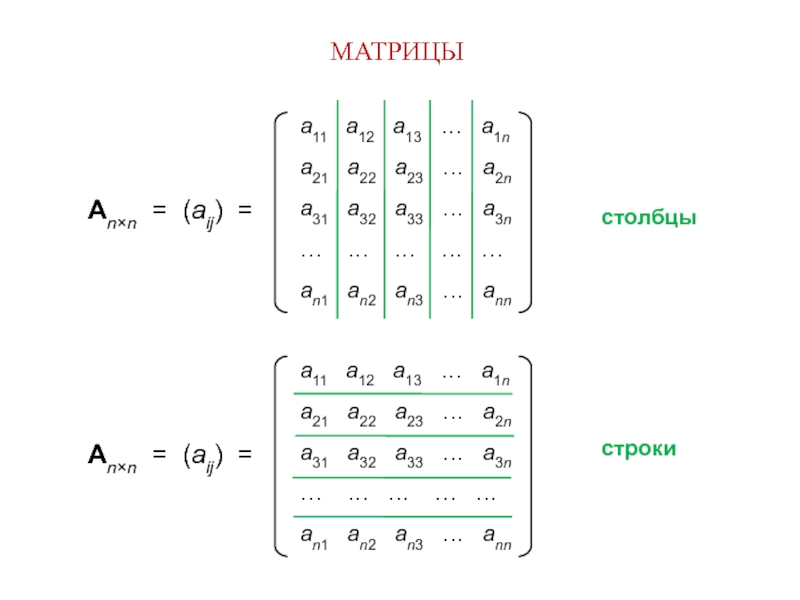
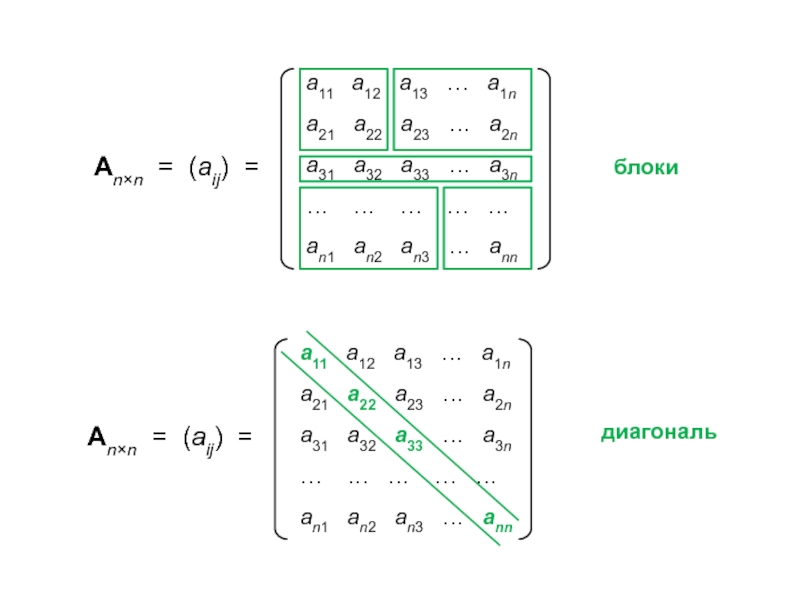
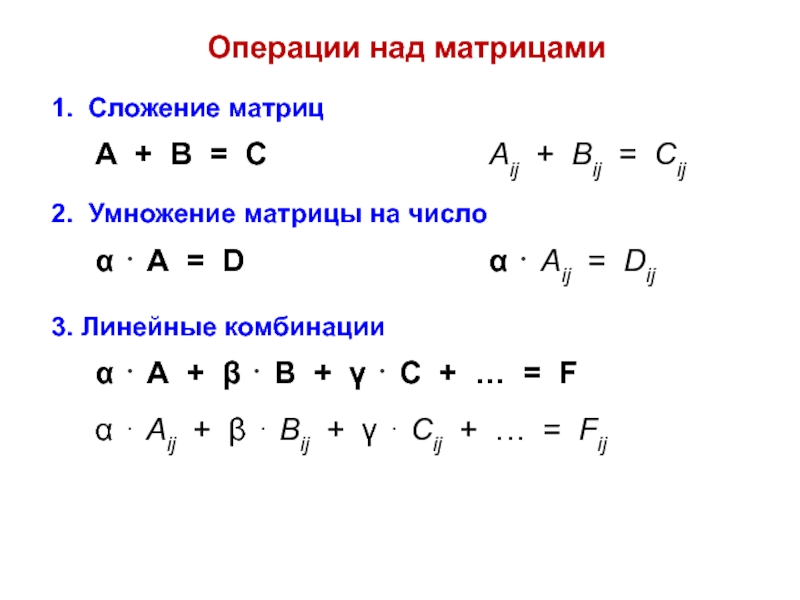
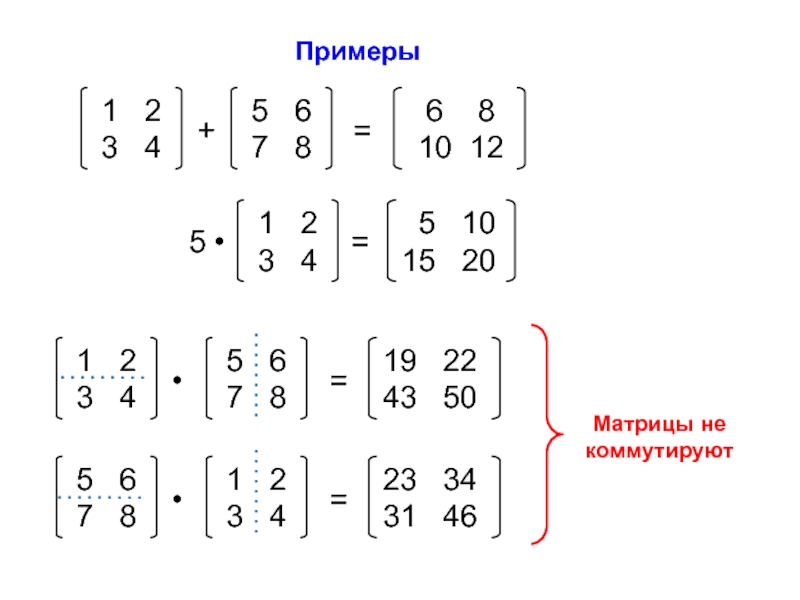
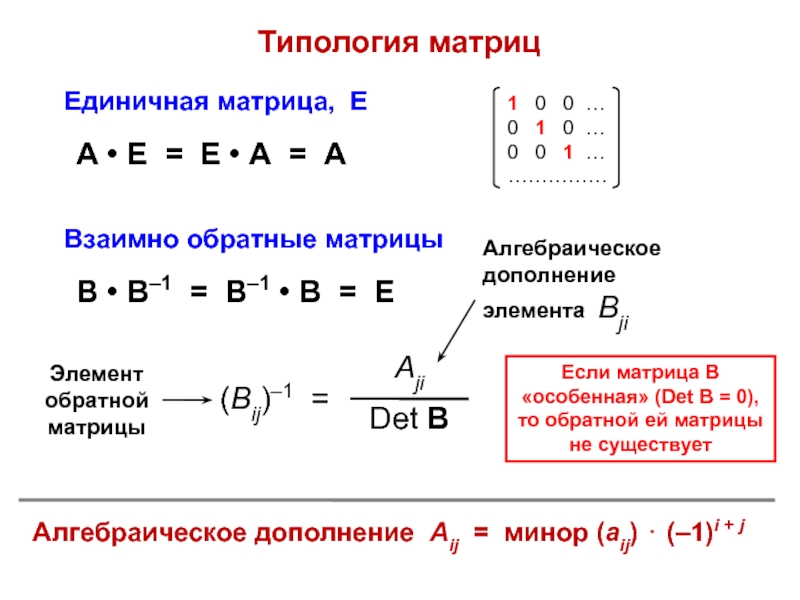
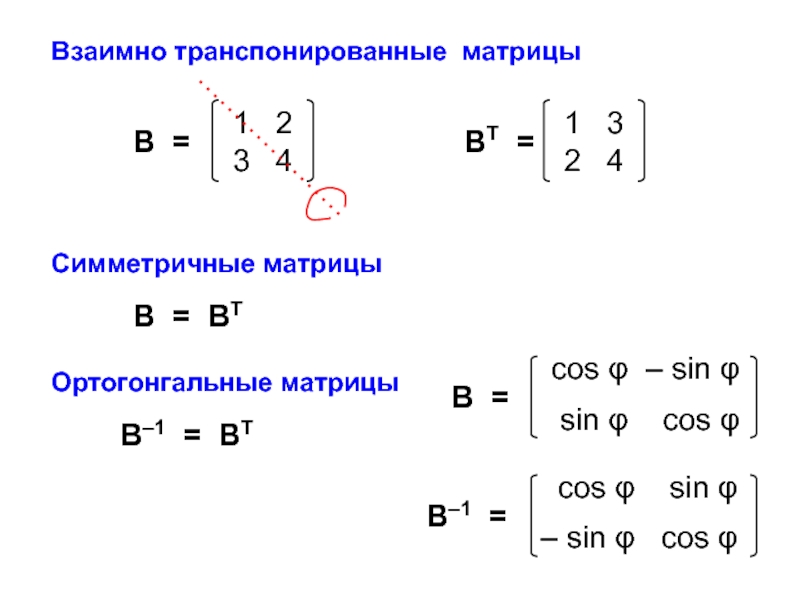
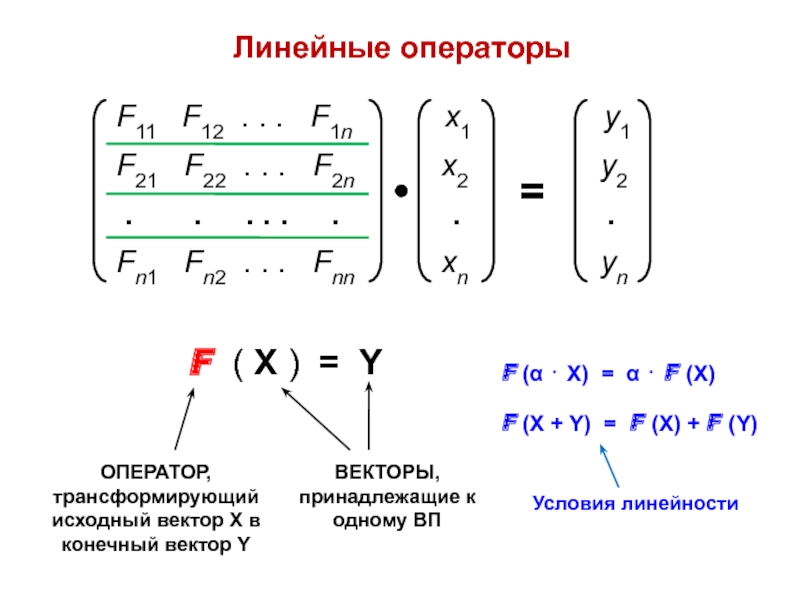
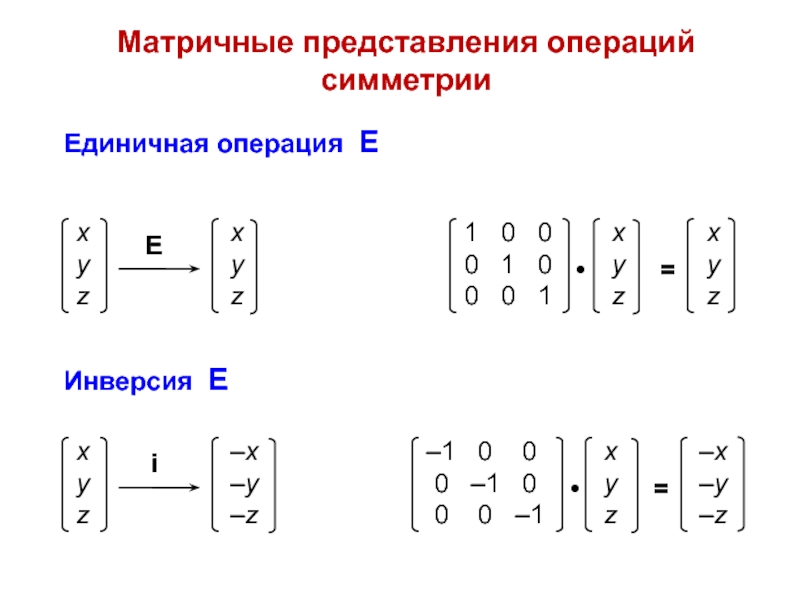
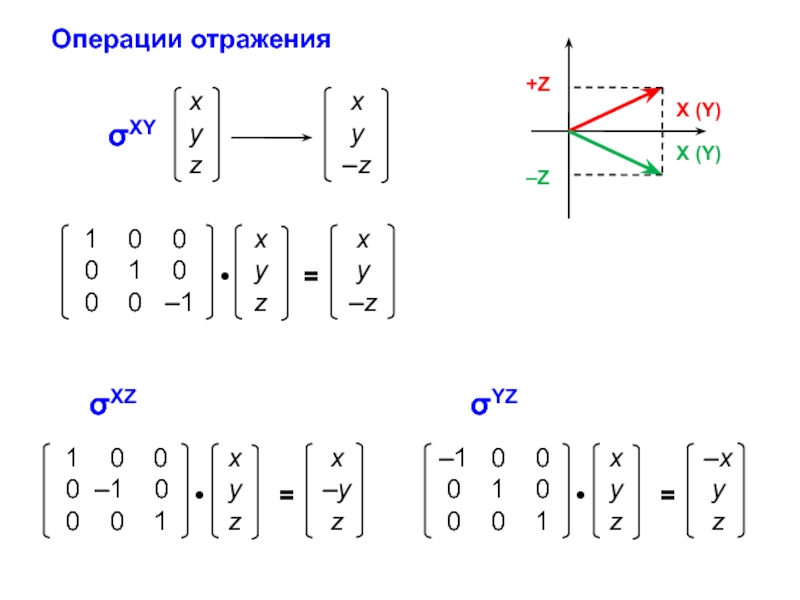
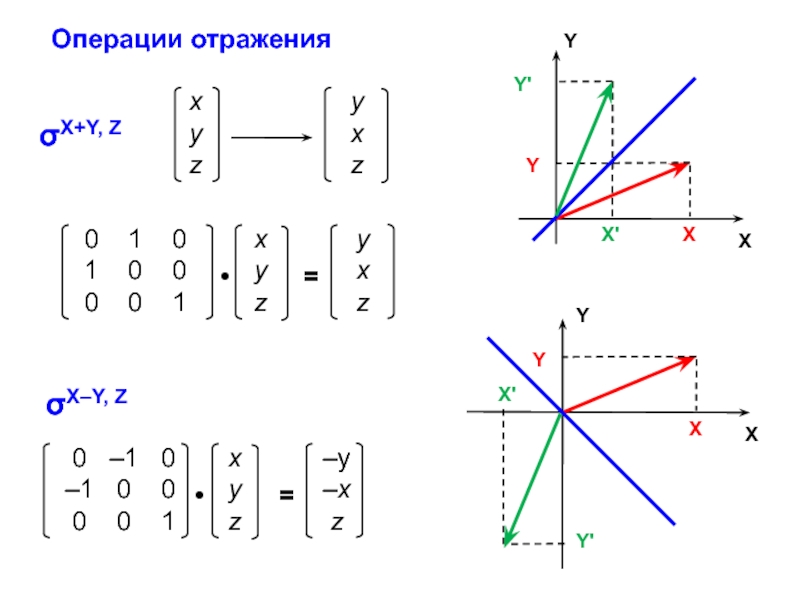
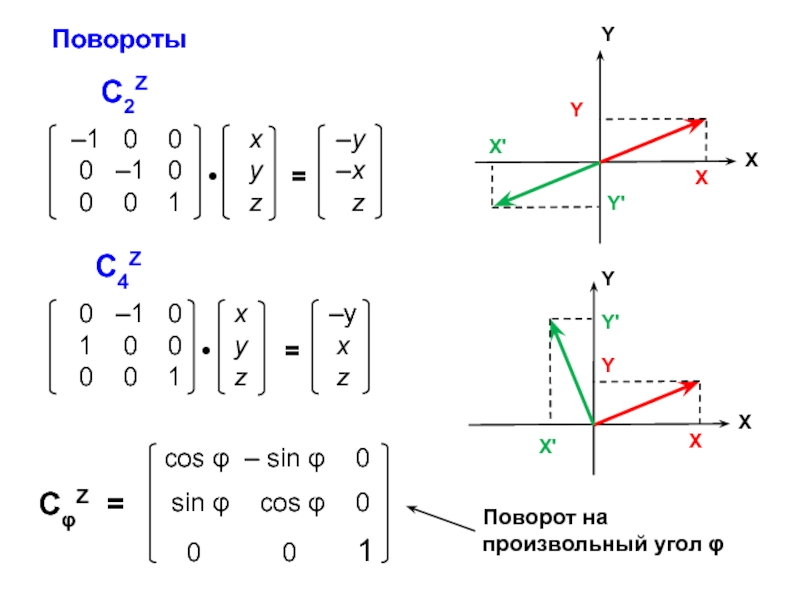
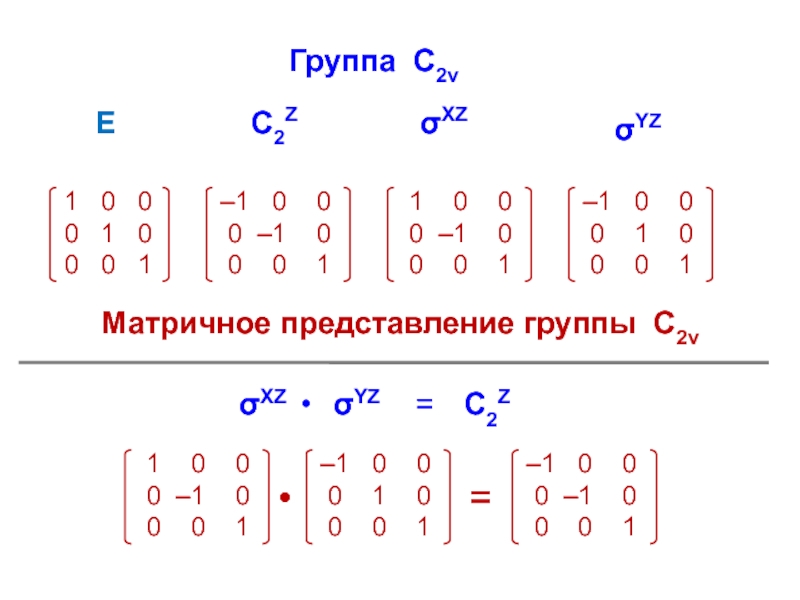
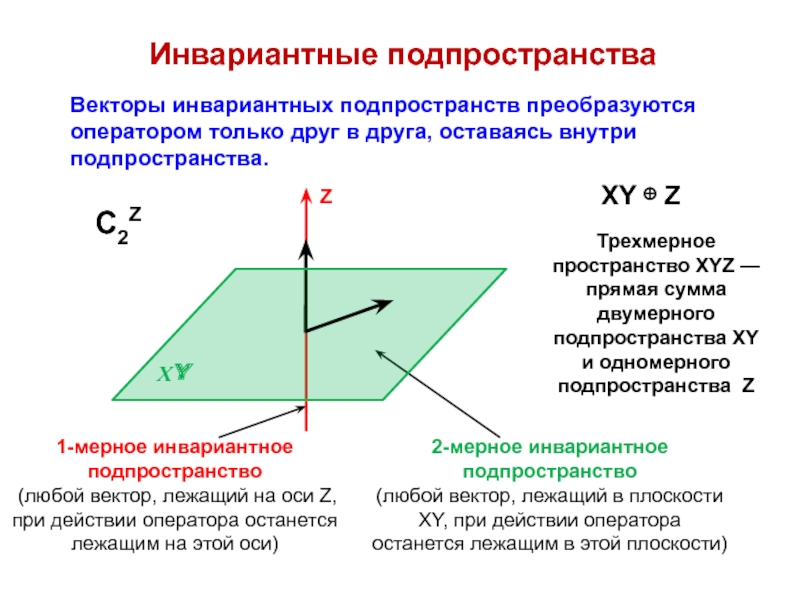
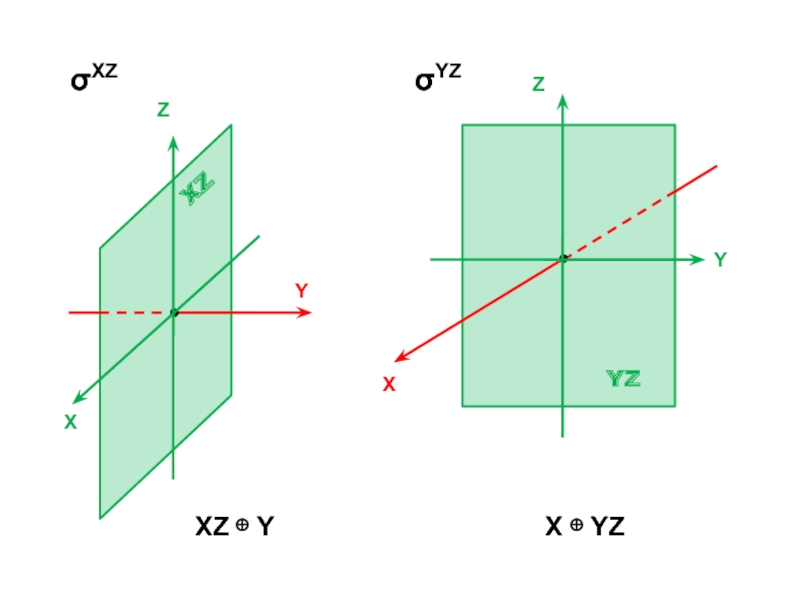
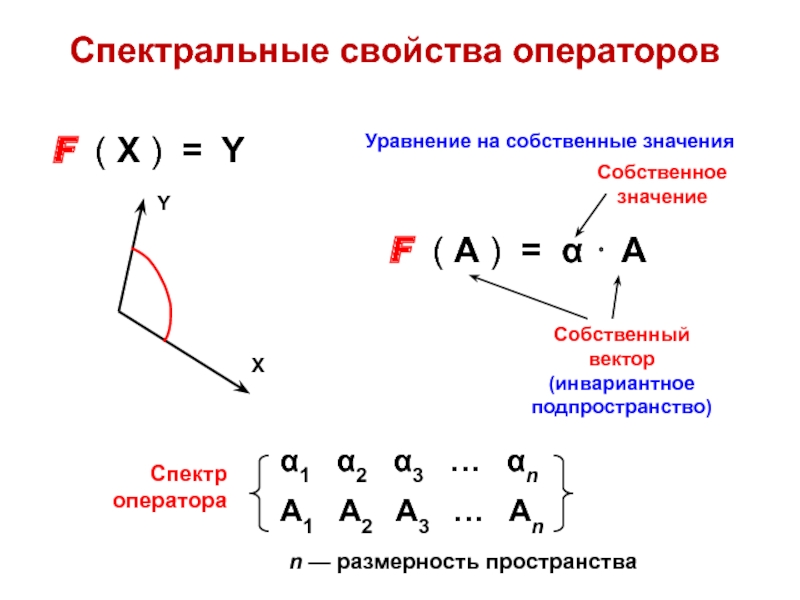
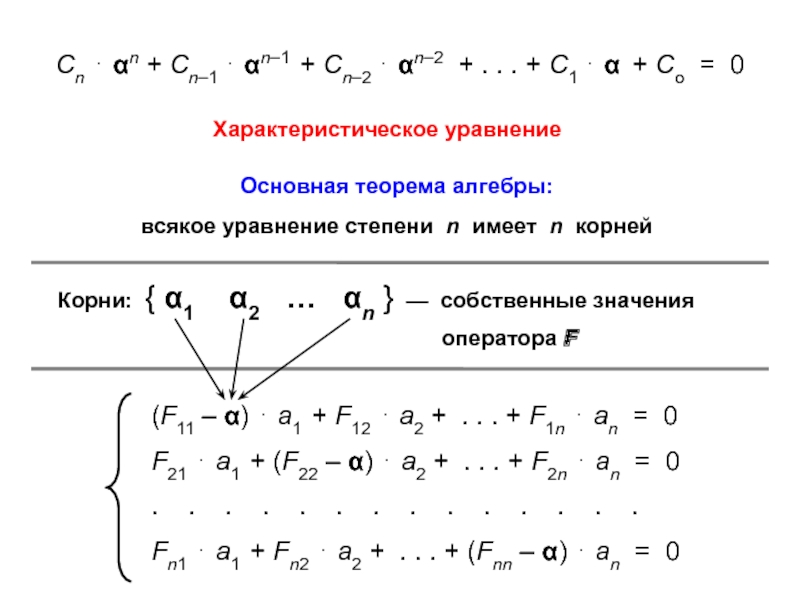
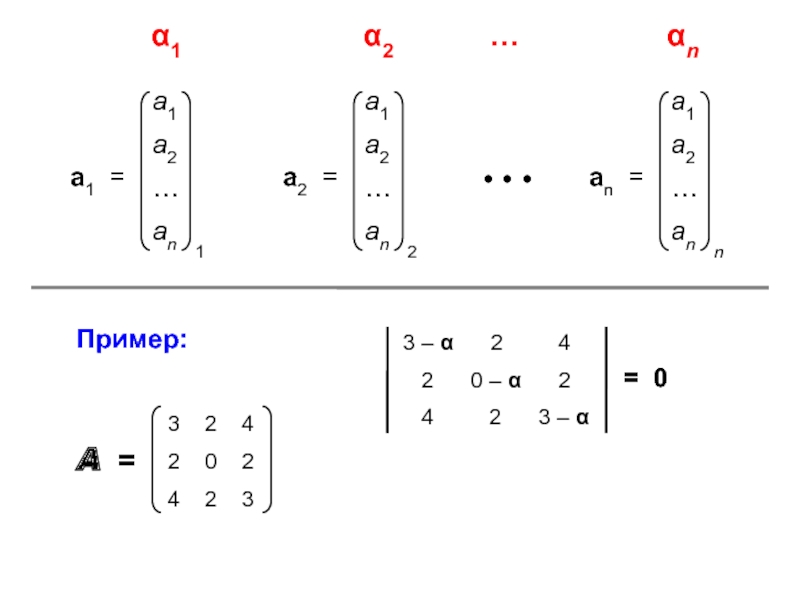
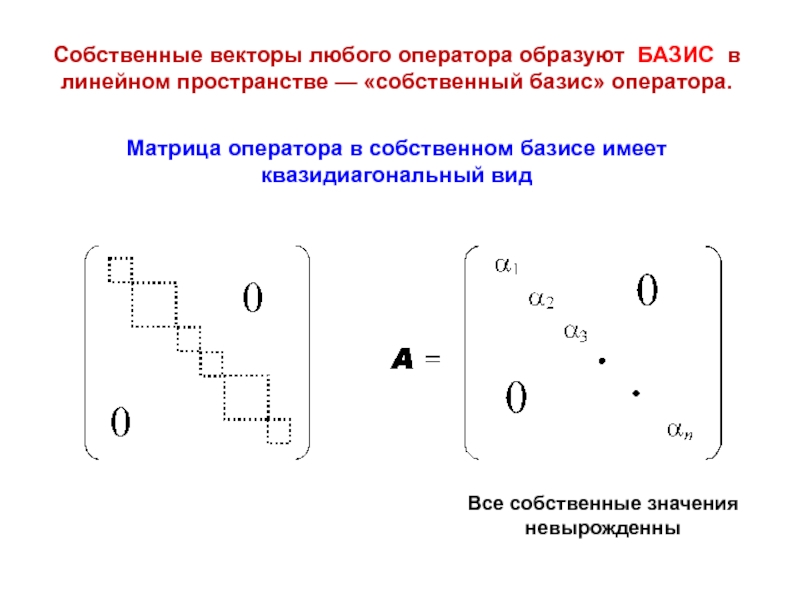
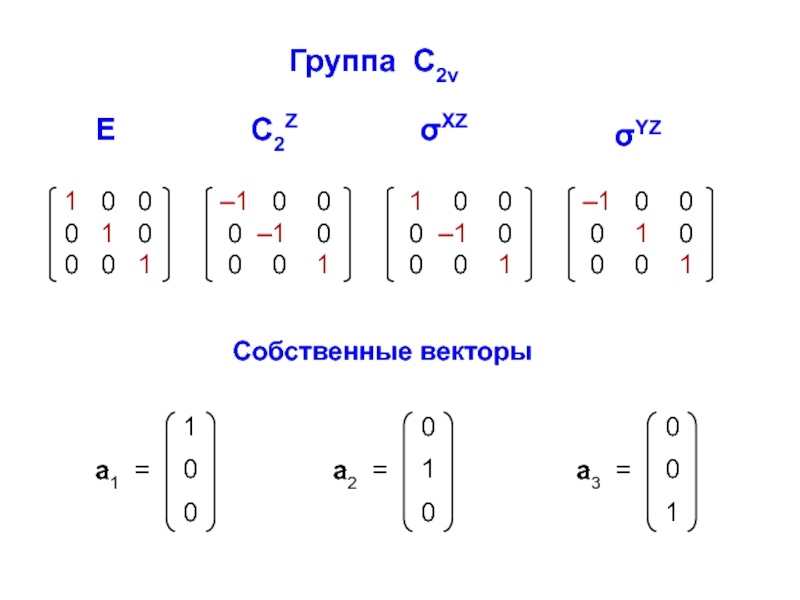
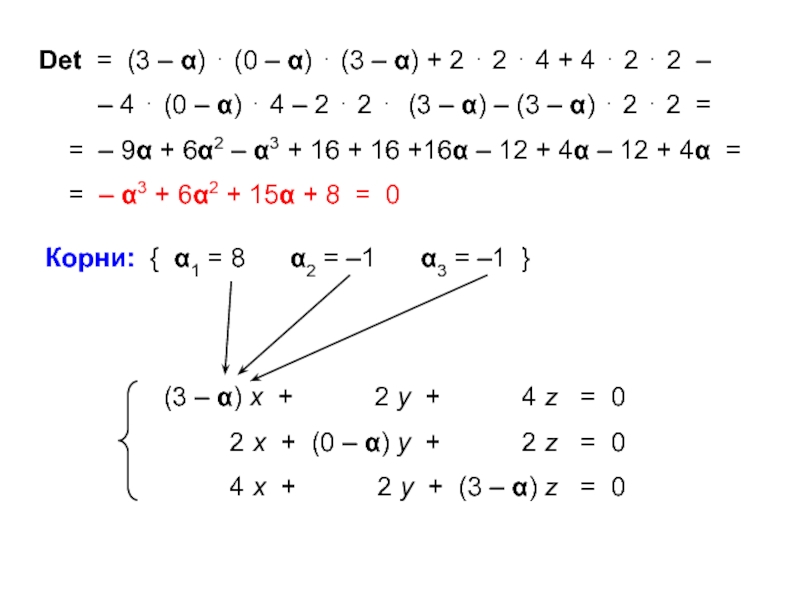ann = ∑ aii
2. Определитель (детерминант)
Метод разложения по элементам строки

1) выбрать в матрице некоторую строку (обычно выбирается та строка, которая содержит наибольшее количество нулей);

2) записать первый элемент выбранной строки и умножить его на вспомогательную матрицу (минор), которая получается из исходной посредством вычеркивания строки и столбца, на пересечении которых стоит выписанный элемент;

j — индексы элемента выделенной строки.

– 1), в результате чего каждый из них превратится в

1) – 4 ⋅ (3 ⋅ 5 – 7 ⋅

= 2 ⋅ (25 – 7) – 4 ⋅ (15 – 28) + 8 ⋅ (3 – 20) =
= 2 ⋅ (18) – 4 ⋅ (–13) + 8 ⋅ (–17) = 36 + 52 – 136 = – 48

Det A = –48

3. Перманент (плюс-определитель)

Метод вычисления тот же самый, что и для определителя, но вместо дополнительного множителя (–1)i+j используется множитель (+1)i+j

1) + 4 ⋅ (3 ⋅ 5 + 7 ⋅

= 2 ⋅ (25 + 7) + 4 ⋅ (15 + 28) + 8 ⋅ (3 + 20) =
= 2 ⋅ (32) + 4 ⋅ (43) + 8 ⋅ (23) = 64 + 172 + 184 = 420

Per A = 420

матрицы на число
α ⋅ А = D
3. Линейные комбинации
α ⋅

= Е
Если матрица В «особенная» (Det В = 0), то

Алгебраическое дополнение элемента Вji

Элемент обратной матрицы

+4/–2 = –2
(В12)–1 = –2/–2 = +1
(В21)–1 = –3/–2 =

Det B = –2

Проверка: В • В–1 = Е

В+
Унитарные матрицы
Аналоги симметричных матриц
Аналоги ортогональных матриц

оператор может быть изображен в виде квадратной матрицы
Единичный оператор
Оператор растяжения
Оператор

симметрии, найти коммутатор.
1) найти матричные представления операций F1 и F2;

оставаясь внутри подпространства.
C2Z
2-мерное инвариантное подпространство
(любой вектор, лежащий в

XY ⊕ Z

Трехмерное пространство XYZ — прямая сумма двумерного подпространства XY и одномерного подпространства Z

) = α ⋅ А
Собственный вектор (инвариантное подпространство)
Собственное значение
Уравнение на

Спектр оператора

n — размерность пространства

+ F12 ⋅ а2 + . . . + F1n

. . . + F1n ⋅ аn = 0
F21 ⋅

Однородная система линейных уравнений

Условие разрешимости: Det = 0

αn–2 + . . . + С1 ⋅ α +

Характеристическое уравнение

Основная теорема алгебры:
всякое уравнение степени n имеет n корней

Корни: { α1 α2 … αn } — собственные значения оператора F

(F11 – α) ⋅ а1 + F12 ⋅ а2 + . . . + F1n ⋅ аn = 0
F21 ⋅ а1 + (F22 – α) ⋅ а2 + . . . + F2n ⋅ аn = 0
. . . . . . . . . . . . . .
Fn1 ⋅ а1 + Fn2 ⋅ а2 + . . . + (Fnn – α) ⋅ аn = 0

α2

• • •

Пример:

(3 – α) + 2 ⋅ 2 ⋅ 4 +

Корни: { α1 = 8 α2 = –1 α3 = –1 }

9z = 0 или x = z
Подставим

Решение:

= 0
2 x + 1 y + 2 z =

Видно, что все три уравнения одинаковы и задают только одно соотношение между тремя неизвестными. Поэтому мы можем произвольно выбрать значения двух неизвестных, а третье уже выразить через эти два.

Уравнение 2x + 1y + 2z = 0 определяет некоторую плоскость (двумерное инвариантное подпространство) в трехмерном пространстве. Любой вектор, лежащий на этой плоскости является решением нашей системы и, следовательно, будет собственным для нашего оператора.

Экономный способ задать все эти векторы заключается в выборе базиса — двух ортогональных векторов на плоскости.

0 и у = 1. Тогда из уравнения плоскости
2x +

Второй базисный вектор должен удовлетворять как уравнению плоскости (2x + 1y + 2z = 0), так и условию ортогональности:

Решая совместно эти два уравнения, получим: у = –2/5 х и z = –4/5 х.

Проверка

= = (+8) ⋅

А (а1) = α1 ⋅ а1

«собственный базис» оператора.
Матрица оператора в собственном базисе имеет квазидиагональный вид


Все

собственные векторы:
α1 = ?

(все собственные значения являются целыми числами)