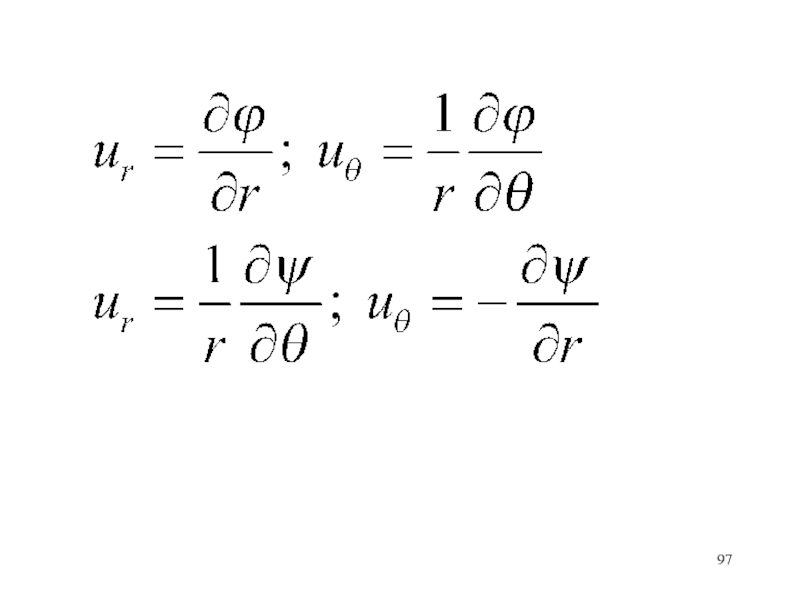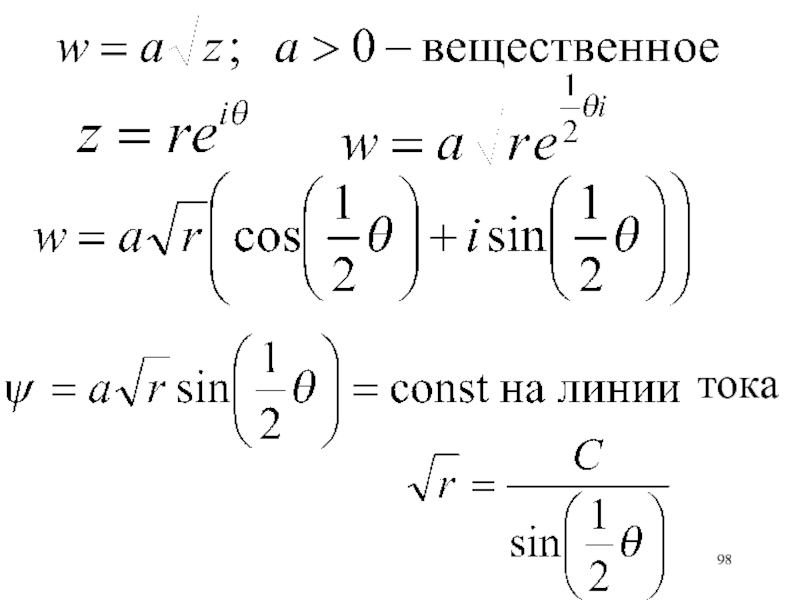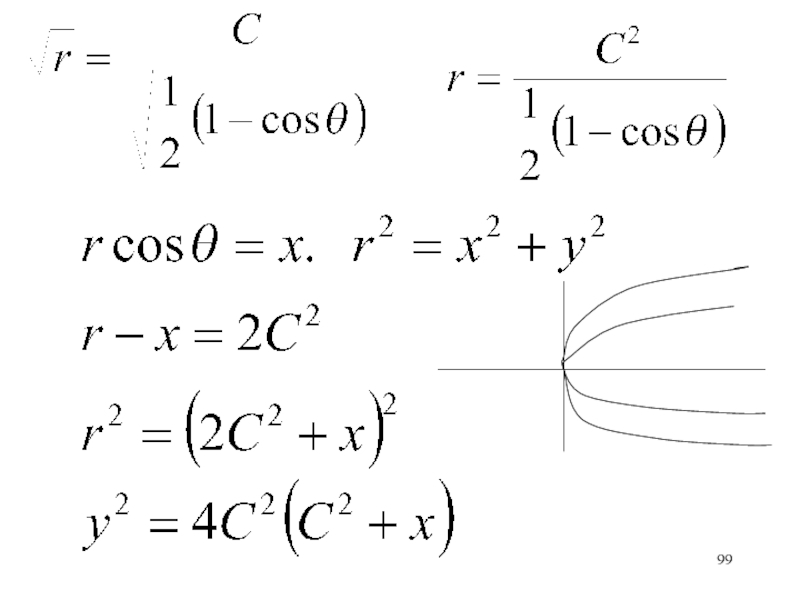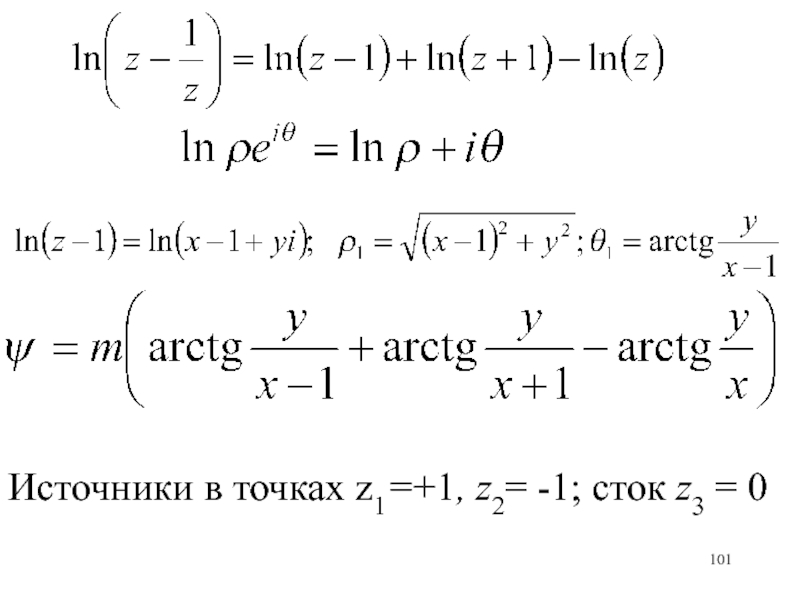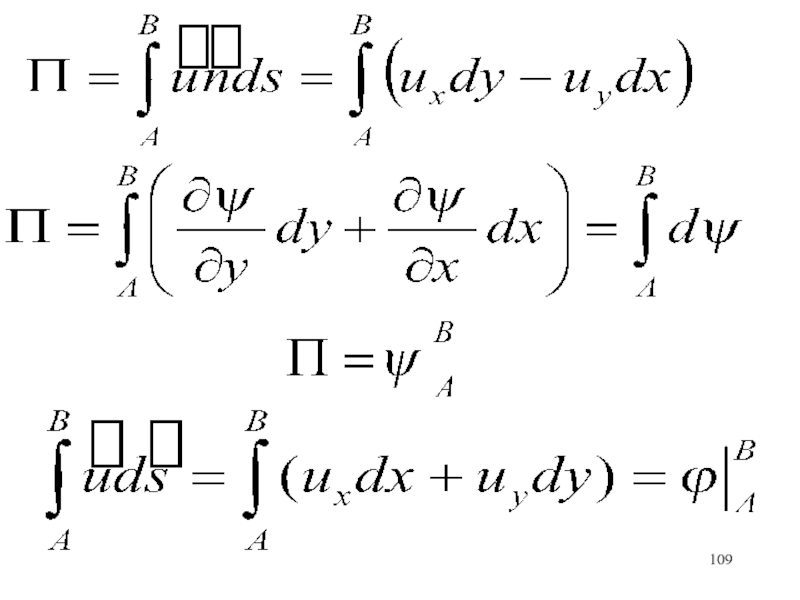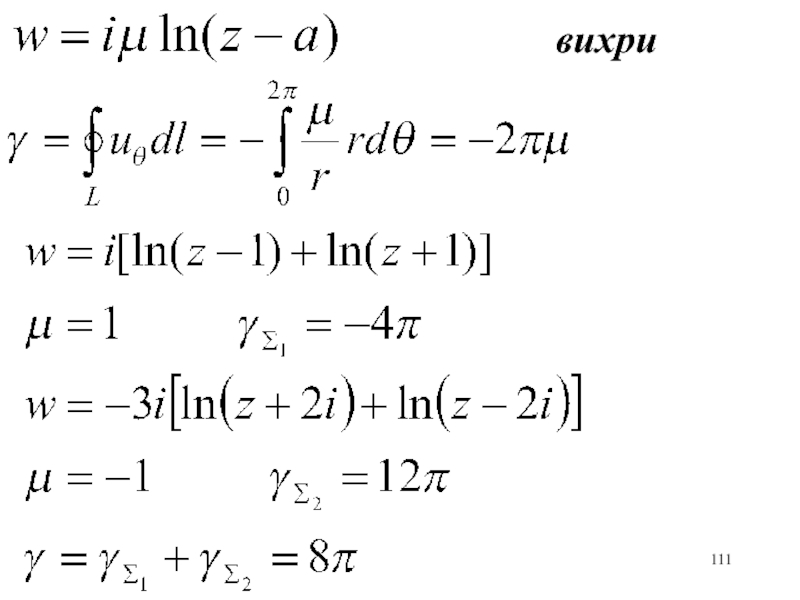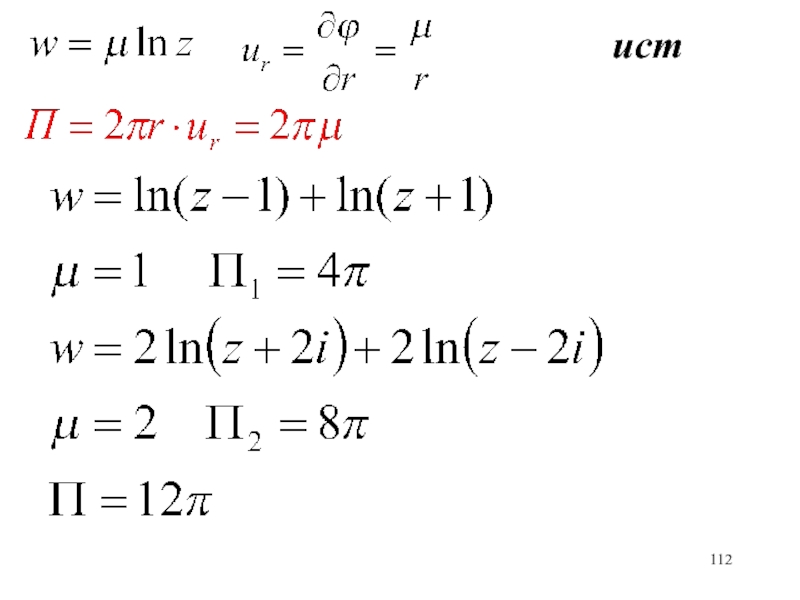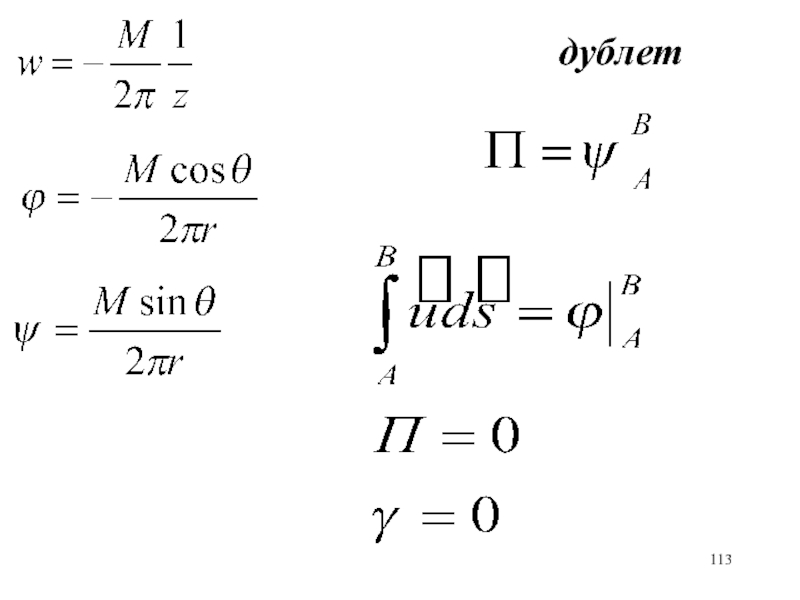Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Эйлер, Ляпунов, Навье и Стокс
Содержание
- 1. 1 Эйлер, Ляпунов, Навье и Стокс
- 2. На участке трубы постоянного диаметра длиной 2м
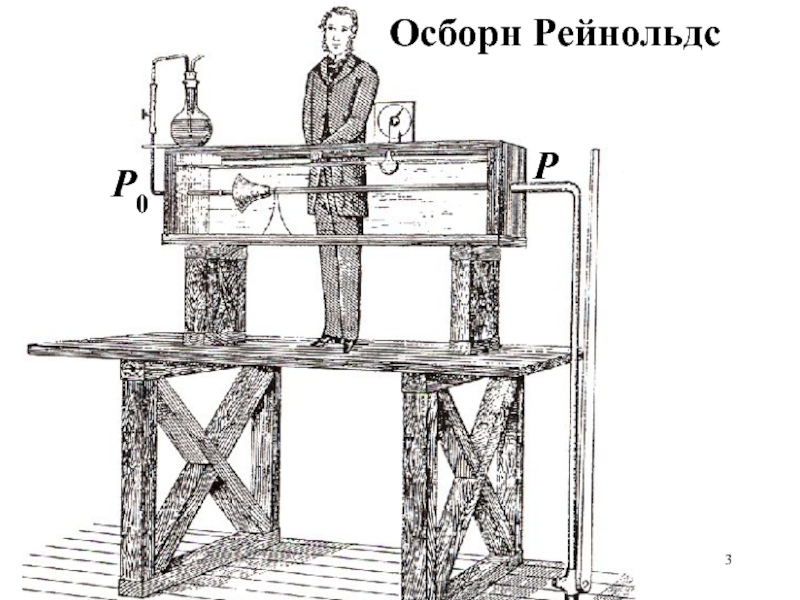
- 3. Осборн РейнольдсP0P
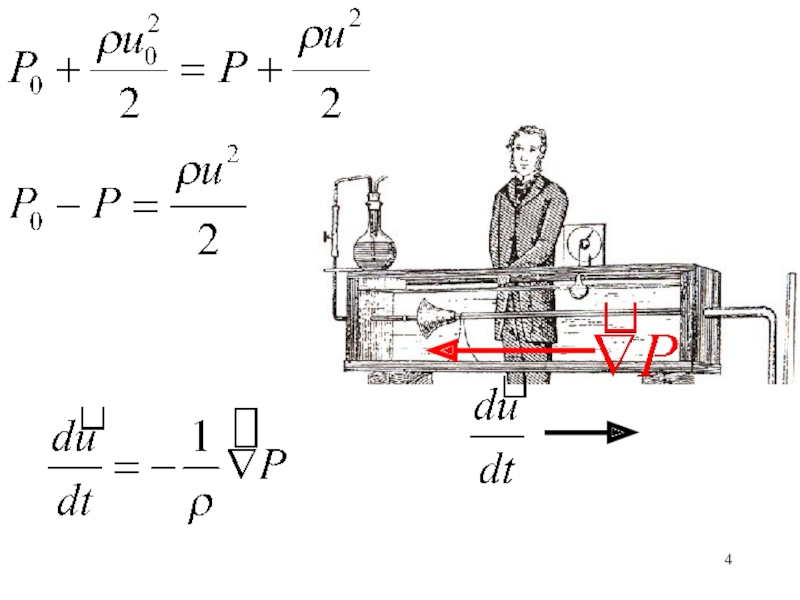
- 4. Слайд 4
- 5. Пример №7Найти потенциал скорости и функцию тока
- 6. Пример №7Найти линии тока и линии равного потенциала
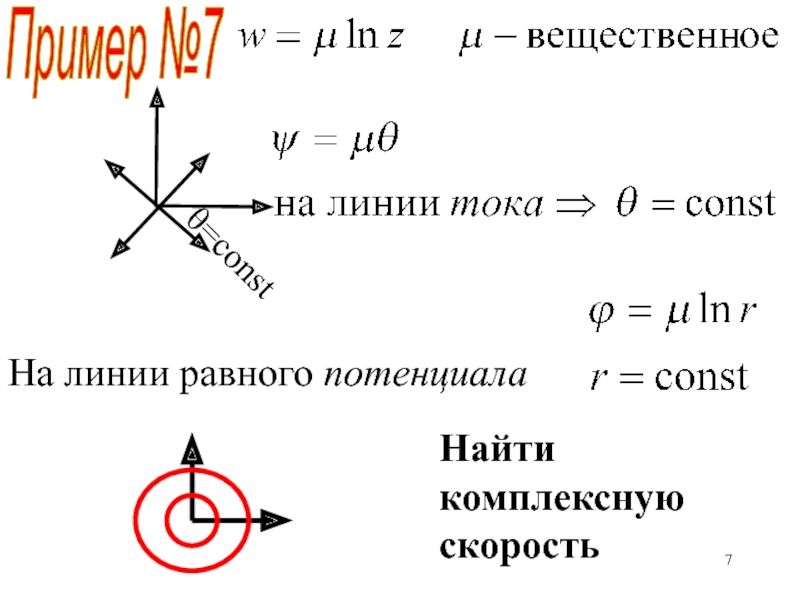
- 7. =constНа линии равного потенциалаПример №7Найти комплексную скорость
- 8. В начале координат особая точка для скорости
- 9. Линии равной скоростиконцентрические окружности. В начале
- 10. Источник из начала координат. Определить поток массы в единицу времени через окружность радиуса r.=constГидродинамическое истолкование потенциала
- 11. Мощность источника 2Поток массы (мощность источника), проходящий
- 12. Если в точках плоскости z = a1,
- 13. xaiyw(z)?
- 14. Точка на комплексной плоскости полностью определяется радиус-вектором
- 15. хх1х2у1у2Чему равен угол θ?
- 16. Слайд 16
- 17. aДва источника мощностью 2 находятся в точках
- 18. aa1iy
- 19. -aa2iy
- 20. a-а i
- 21. a2iy
- 22. a1iy
- 23. Слайд 23
- 24. az = -а iМнимая ось – линия тока
- 25. Два источника мощностью 2 находятся в точках
- 26. Слайд 26
- 27. Определить поток скорости и ротор скорости по
- 28. систочник мощностью 2 находится в точке (с).
- 29. Стенку заменяем линией тока. Для этого помещаем
- 30. zс-сОпределяем функцию тока в точке
- 31. а iz=bc-cПоловина всего потока массыОпределяем функцию тока в точке
- 32. систочник мощностью 2 находится в точке (с),
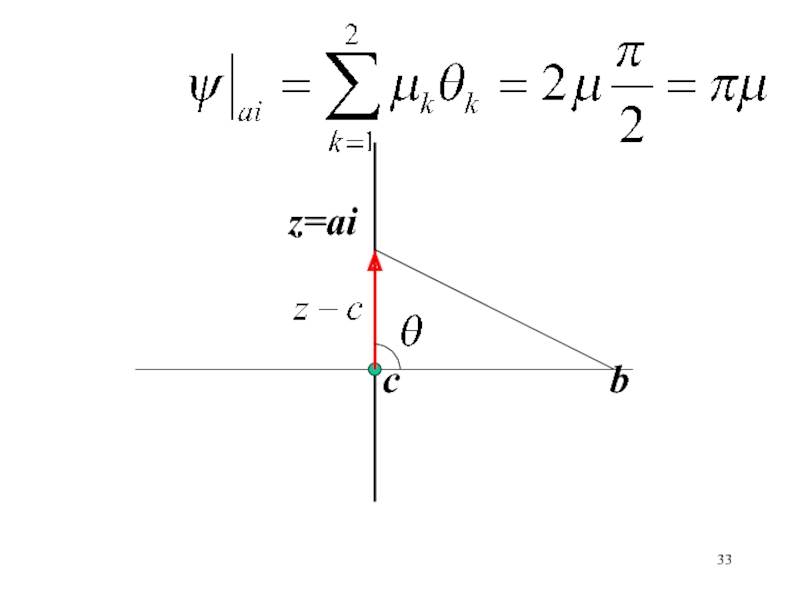
- 33. сz=aib
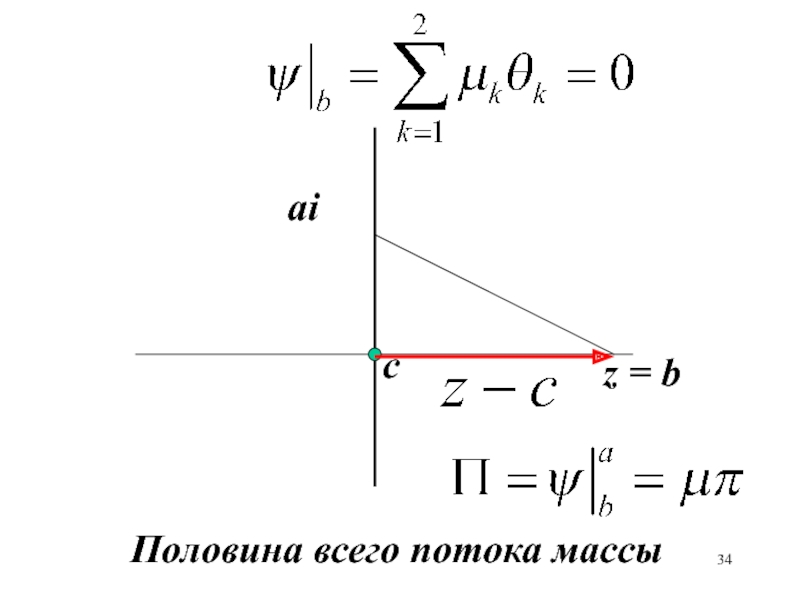
- 34. сaiz = bПоловина всего потока массы
- 35. В начале координат помещен источник интенсивности 2
- 36. Слайд 36
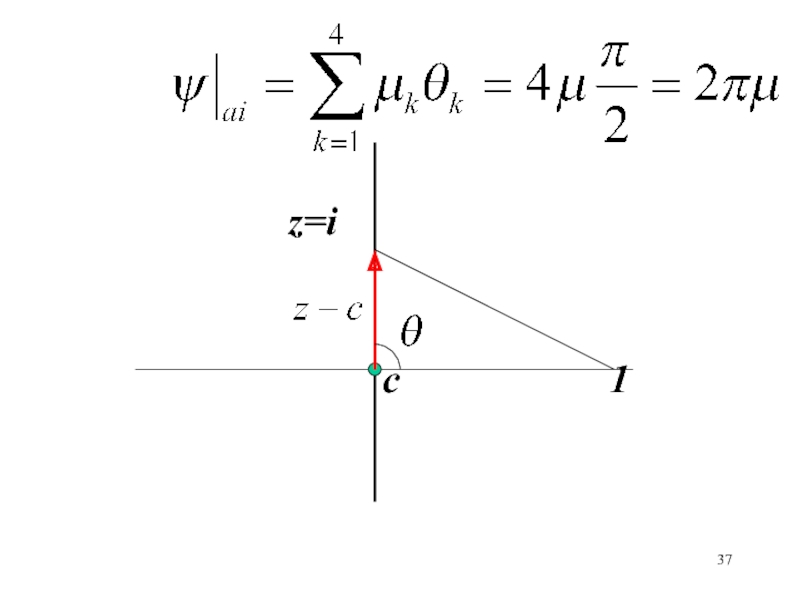
- 37. сz=i1
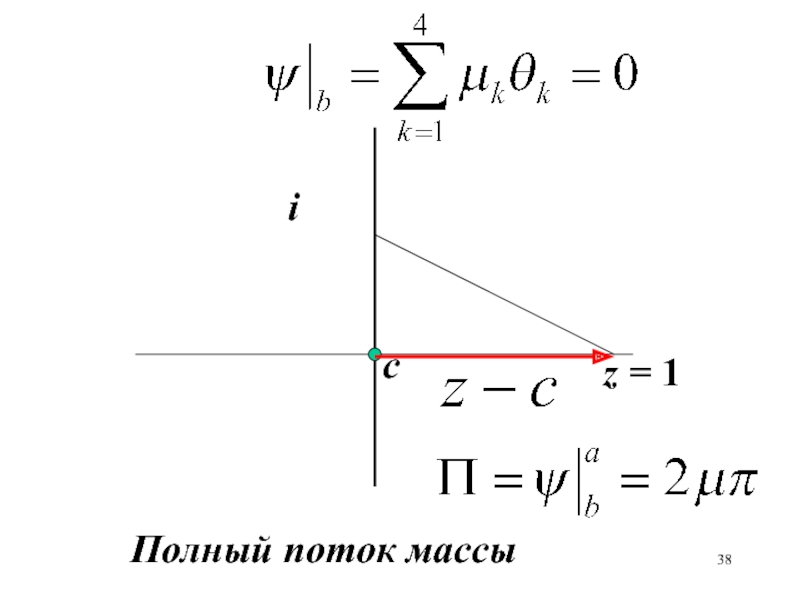
- 38. сiz = 1Полный поток массы
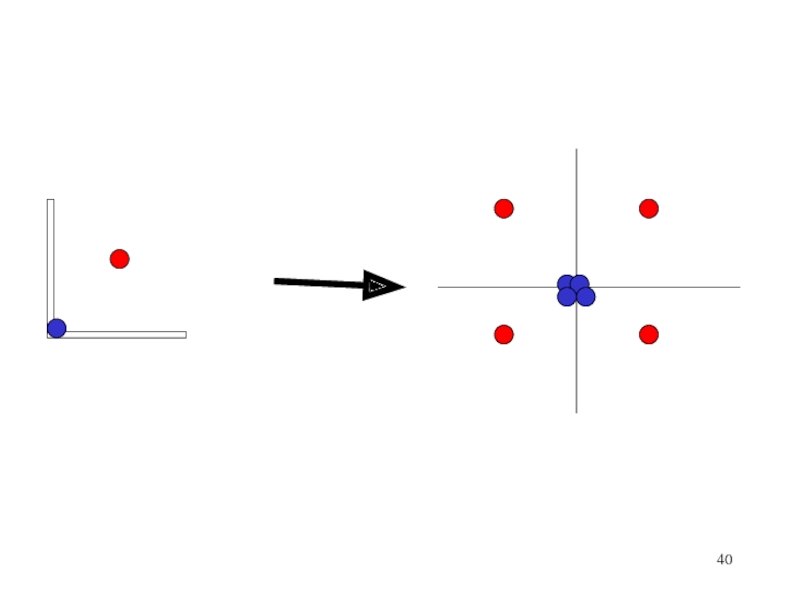
- 39. В точке z=1+i имеeтся источник интенсивности 2
- 40. Слайд 40
- 41. Слайд 41
- 42. z=1Найти линии тока
- 43. Слайд 43
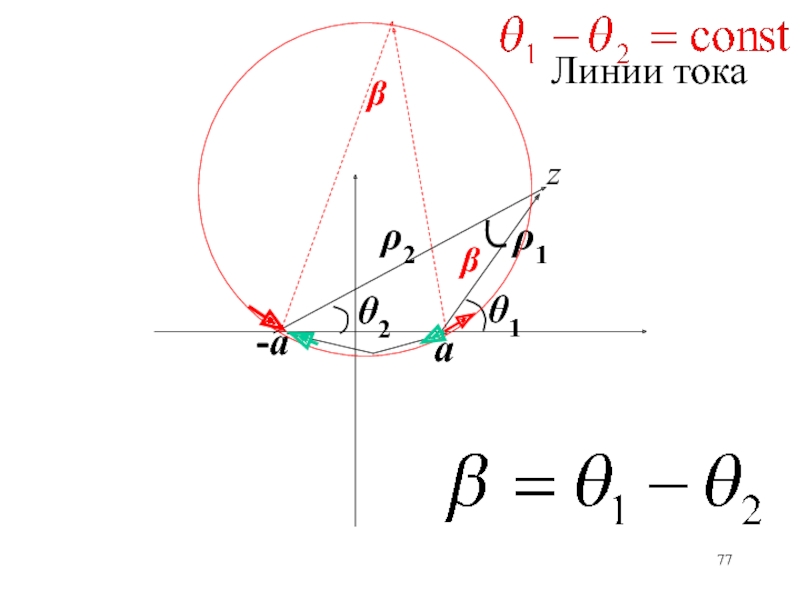
- 44. Линии тока
- 45. Вихревые точки
- 46. Найти линии тока и линии равного потенциала
- 47. Слайд 47
- 48. Линии тока r = const концентрические окружности.Определить компоненты скорости
- 49. Является ли это движение потенциальным? Чтобы узнать это надо определить ротор скорости
- 50. Движение безвихревое везде, кроме начала координат где, Эту точку назовем вихревой.
- 51. Вычислить потенциал скорости для = 0 = 2
- 52. Потенциал скорости - неоднозначная функция координат на
- 53. Определить циркуляцию скорости
- 54. Скорость:Циркуляция скорости по замкнутому контуру L:Циркуляцию скорости назовем интенсивностью вихревой точкиrdL
- 55. Вихревая точка, расположенная в начале координат z = 0 создает плоское движение, определяемое комплексным потенциалом
- 56. Комплексный потенциалгруппывихревых точек
- 57. Если вихревая точка не в начале координат,
- 58. 1-1iДве вихревые точкиКакой интенсивностью должны обладать точки, чтобы вертикальная ось совпадала с линией тока?
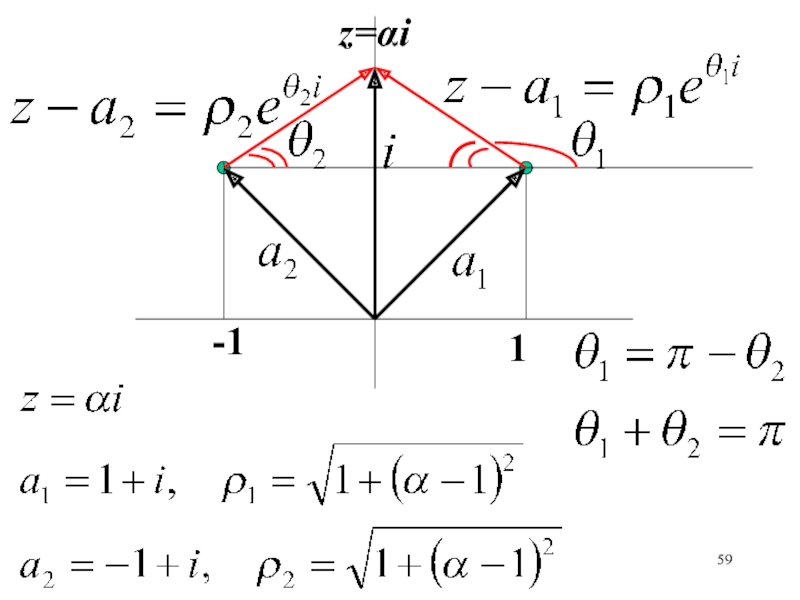
- 59. 1-1z=i
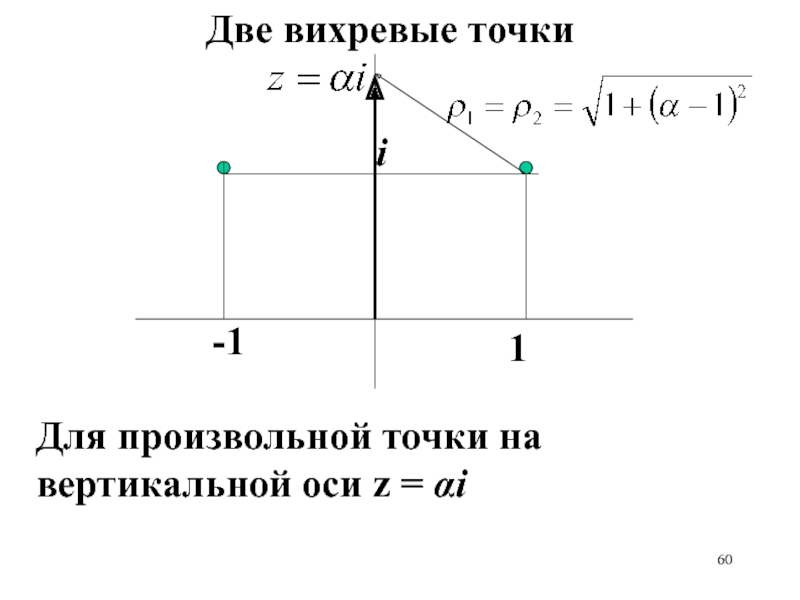
- 60. 1-1iДве вихревые точкиДля произвольной точки на вертикальной оси z = αi
- 61. Слайд 61
- 62. Для любых , т.е. для любых
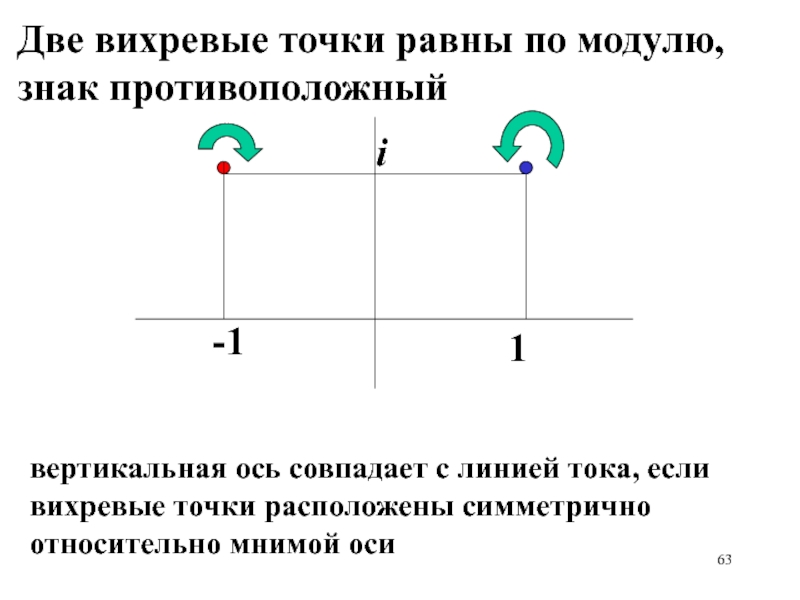
- 63. 1-1iДве вихревые точки равны по модулю, знак
- 64. Исследовать течение жидкости, которое описывается комплексным потенциалом
- 65. Начало координат представляет собой особенность - совокупность вихревой точки интенсивности и источника мощностью m =(2)Вихреисточник
- 66. На линии тока = const:линия тока
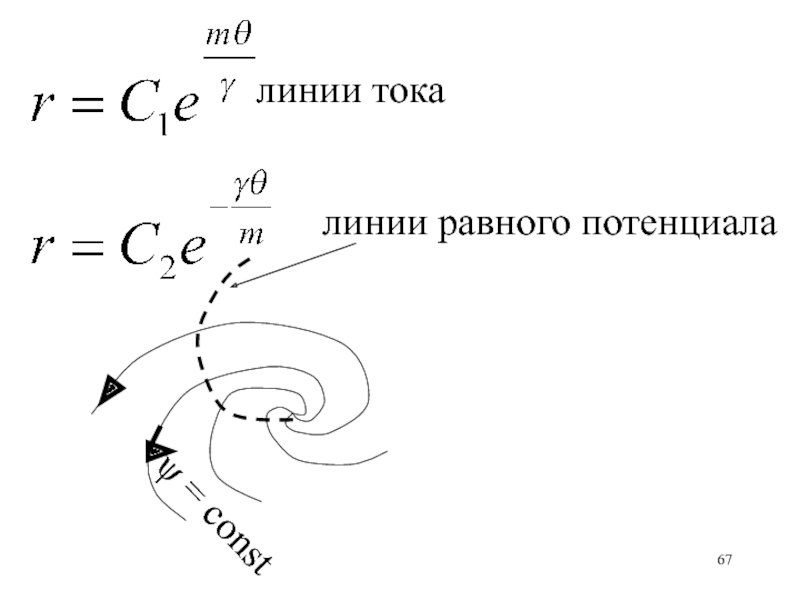
- 67. линии тока линии равного потенциала = const
- 68. Вычеты комплексной скороти,циркуляция и поток скорости
- 69. Структура аналитической функции w(z) вполне определяется распределением
- 70. Если простые полюсы функции U*лежат в точках
- 71. Циркуляция скорости по контуру LПоток скорости через контур L
- 72. Выделим действительную и мнимую часть каждого вычетаТогда получаем
- 73. Какое течение определяет комплексный потенциал?
- 74. Слайд 74
- 75. а-аz2 121
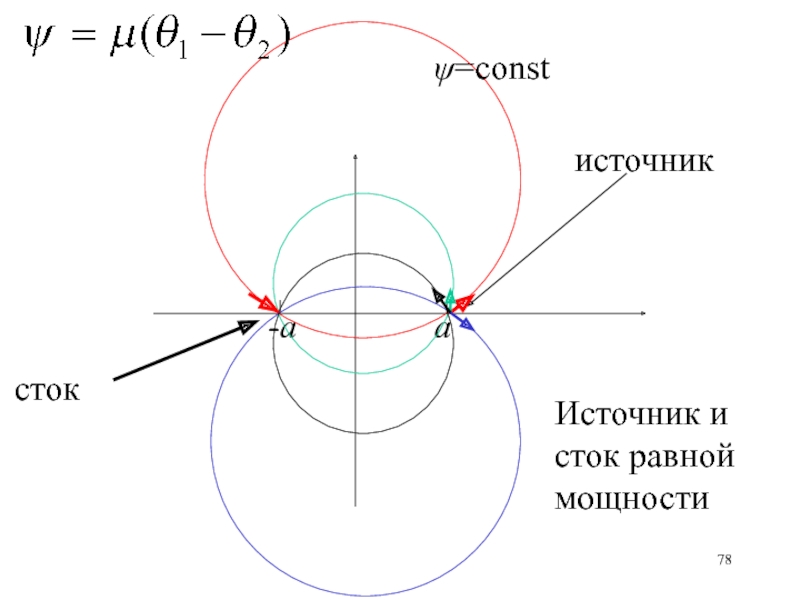
- 76. = const на линии тока
- 77. а-аz2121Линии тока
- 78. а-а=constисточникстокИсточник и сток равной мощности
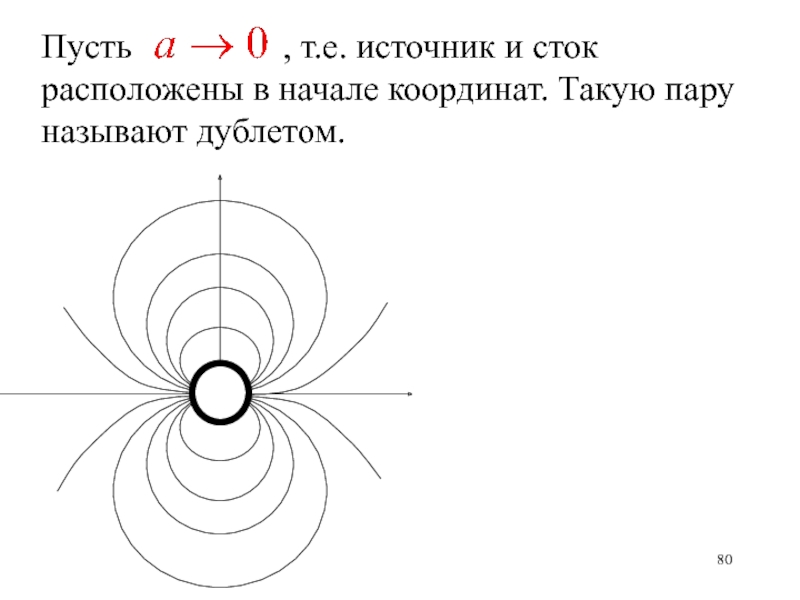
- 79. ДУБЛЕТ
- 80. Пусть
- 81. Пусть малое расстояние между источником и стоком
- 82. Разлагаем в рядПри s 0 получаем для потенциала скоростиДля сопряженной функции тока по формулеОтветЗаписать комплексный потенциал
- 83. Для комплексного потенциала получаемЕсли ось дублета s
- 84. Если на плоскости 0ху в точках z
- 85. Дублет находится в точке z = a,
- 86. i0
- 87. Слайд 87
- 88. Определить поток жидкости через отрезок [-a+i, a+i]Какое течение определяет комплексный потенциал?
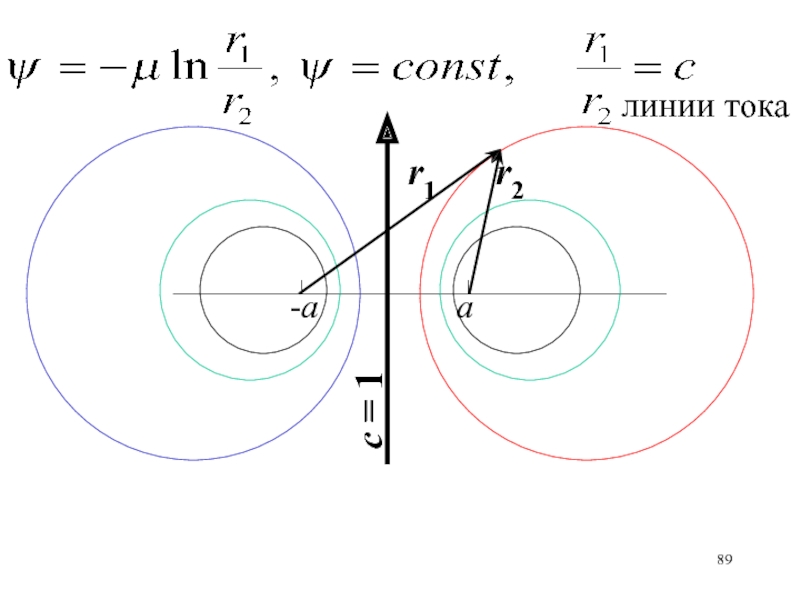
- 89. а-аr1r2с = 1линии тока
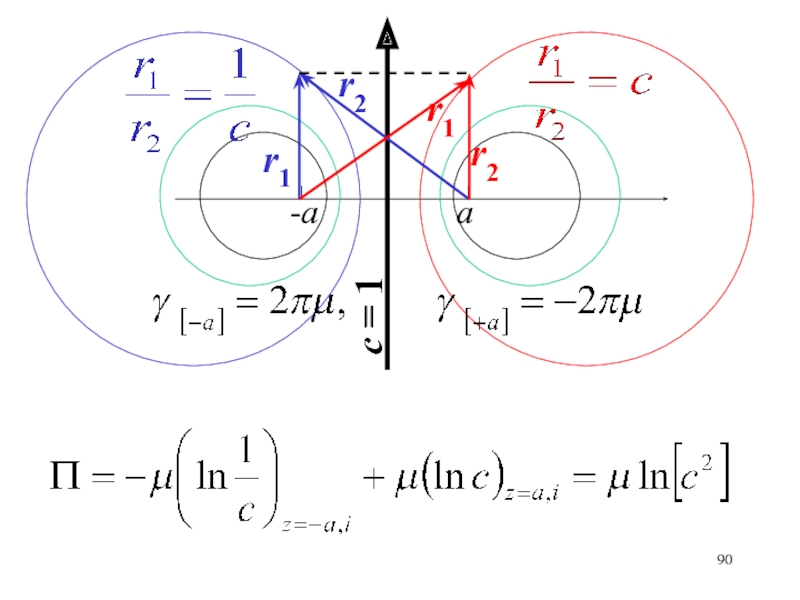
- 90. а-аr1r2с = 1r1r2
- 91. Исследовать течение жидкости (плоское, безвихревое), которое описывается
- 92. Сопряженную функцию тока определяем по формуле
- 93. Слайд 93
- 94. =0=0
- 95. [z1=0, z2=1+i]11хуz1z2
- 96. ЗАДАЧА 1Найти линии тока, получить проекции скорости,
- 97. Слайд 97
- 98. тока
- 99. Слайд 99
- 100. Найти функцию тока. В каких точках находятся
- 101. Источники в точках z1=+1, z2= -1; сток z3 = 0
- 102. Уравнение линий токаЛиниями тока, в частности, являются оси координат и окружность
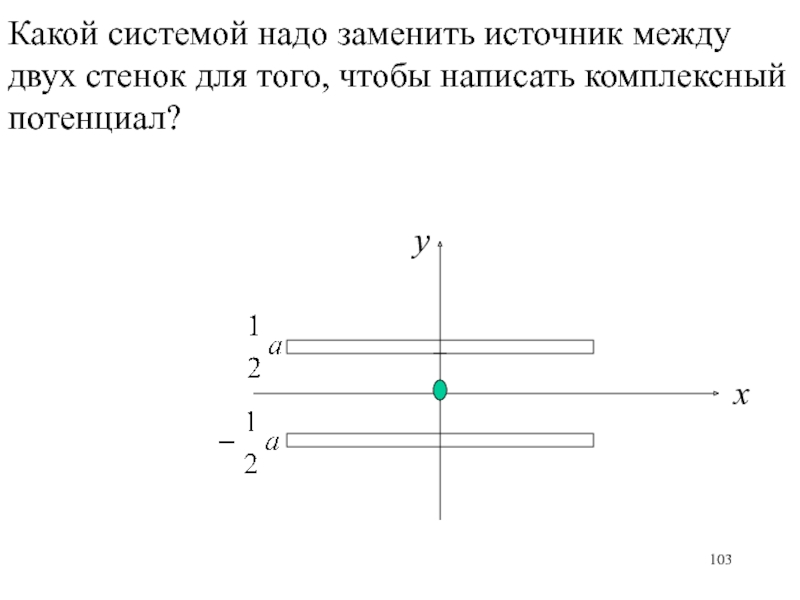
- 103. Какой системой надо заменить источник между двух стенок для того, чтобы написать комплексный потенциал? хy
- 104. Источники одинаковой мощности на равном расстоянии
- 105. Эти же формулы имеют место для источника,
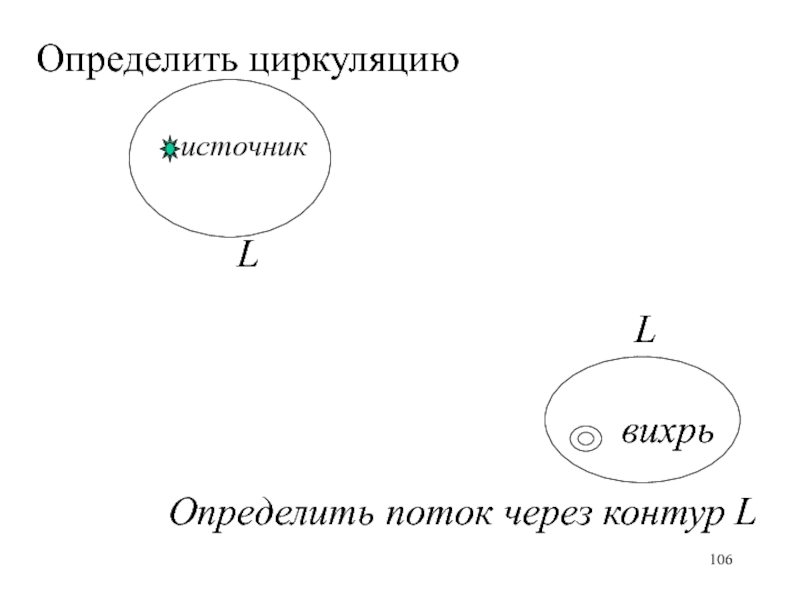
- 106. источникОпределить циркуляциюLLвихрьОпределить поток через контур L
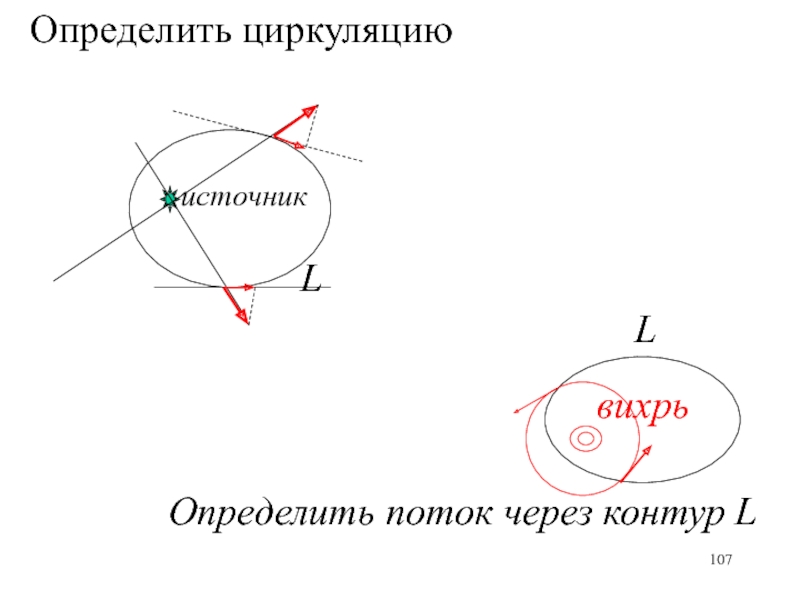
- 107. источникОпределить циркуляциюLLвихрьОпределить поток через контур L
- 108. ЗадачаТечение определяется потенциаломНайти поток жидкости через окружностьИ циркуляцию скорости по этой окружности
- 109. Слайд 109
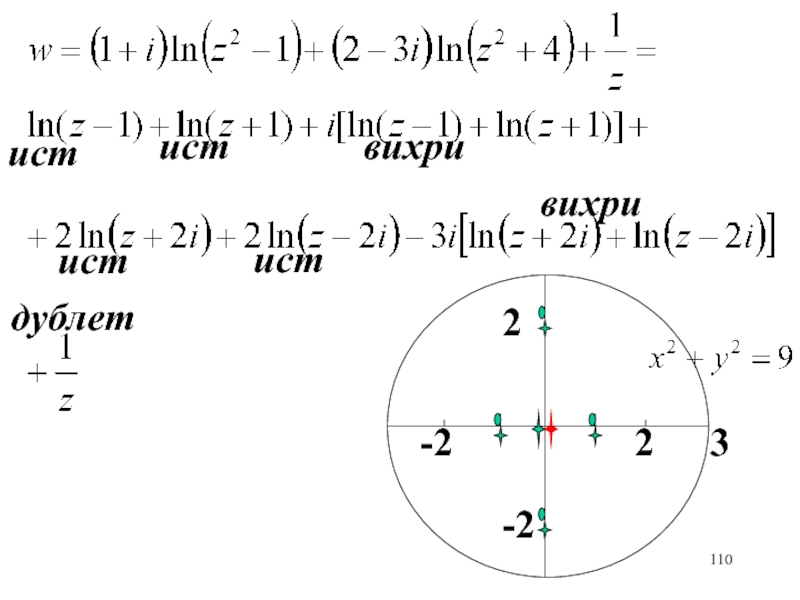
- 110. 2-23-22истистистиствихривихридублет
- 111. вихри
- 112. ист
- 113. дублет
- 114. Слайд 114
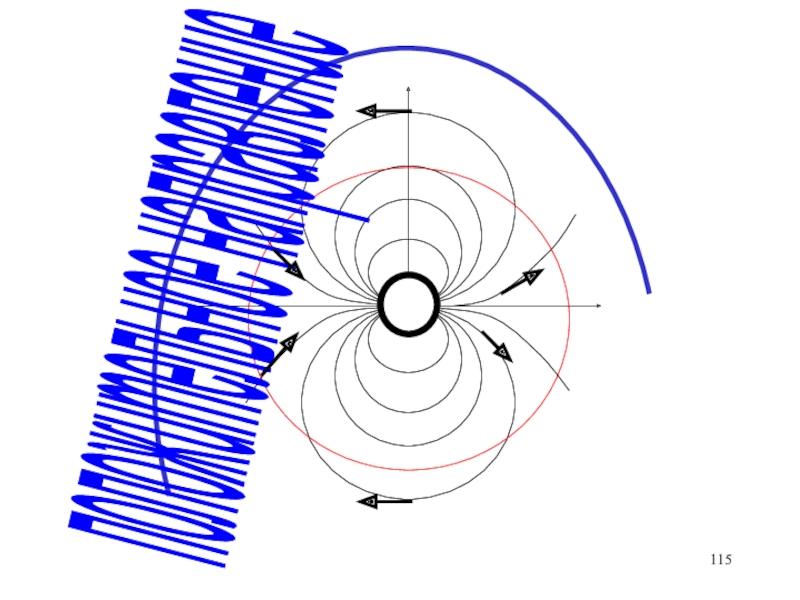
- 115. положительное направление
- 116. Мощность источника 2Поток массы (мощность источника), проходящий
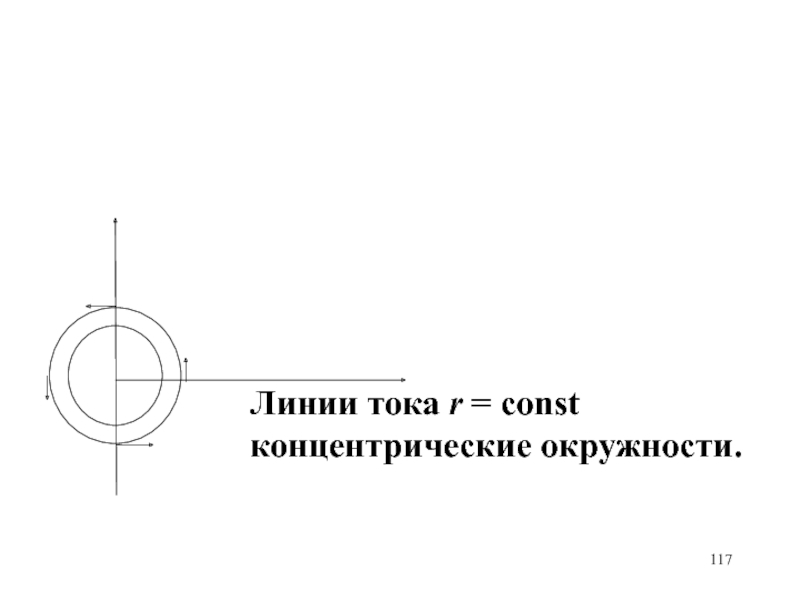
- 117. Линии тока r = const концентрические окружности.
- 118. Скорость:Циркуляция скорости по замкнутому контуру L:Циркуляцию скорости назовем интенсивностью вихревой точкиrLdLПример №9
- 119. ЗАДАЧА 3В верхней полуплоскости имеются 2 источника
- 120. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2На участке трубы постоянного диаметра длиной 2м приложен градиент давления
(линейная зависимость от продольной координаты).
участке, если скорость воды возрастает от 0 до 1 м/с, а движение идеальной жидкости. Куда направлен градиент давления?Слайд 8В начале координат особая точка для скорости и комплексного потенциала.
Исключаем эту точку, окружив произвольной замкнутой линией.
Пример №7
Записать компоненты
скорости. Построить линии равной скоростиСлайд 9Линии равной скорости
концентрические окружности. В начале координат - особая
точка.
Поле скорости непрерывно и конечно во всех точках кроме одной.
Начало должно быть исключено с помощью описанной вокруг него замкнутой кривой.Пример №7
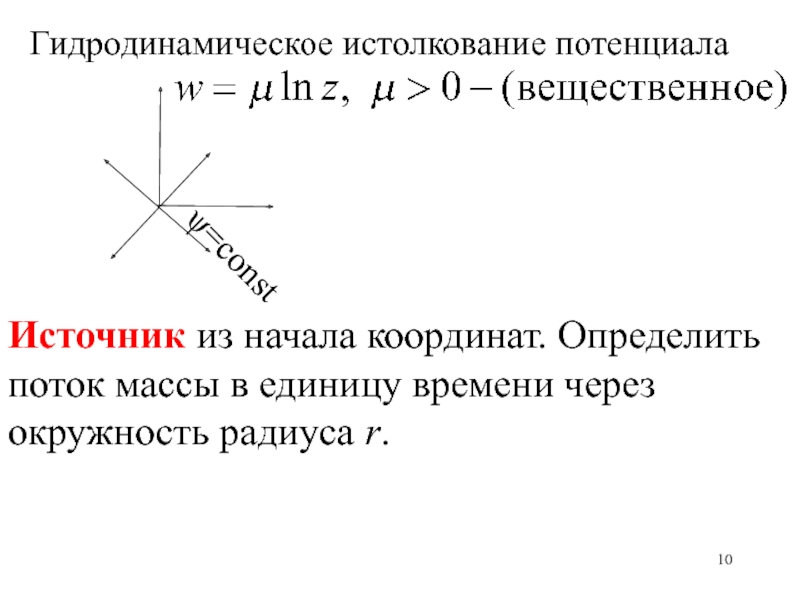
Слайд 10Источник из начала координат. Определить поток массы в единицу времени
через окружность радиуса r.
=const
Гидродинамическое истолкование потенциала
Слайд 11Мощность источника 2
Поток массы (мощность источника), проходящий через окружность радиуса
r в единицу времени, определяется произведением радиальной скорости на длину
окружностине зависит от радиуса (сохранение массы). Если <0, то определяет сток.
Слайд 12Если в точках плоскости z = a1, a2,…an находятся источники
или стоки мощностью 21, 22, …, 2n
k – модуль, k
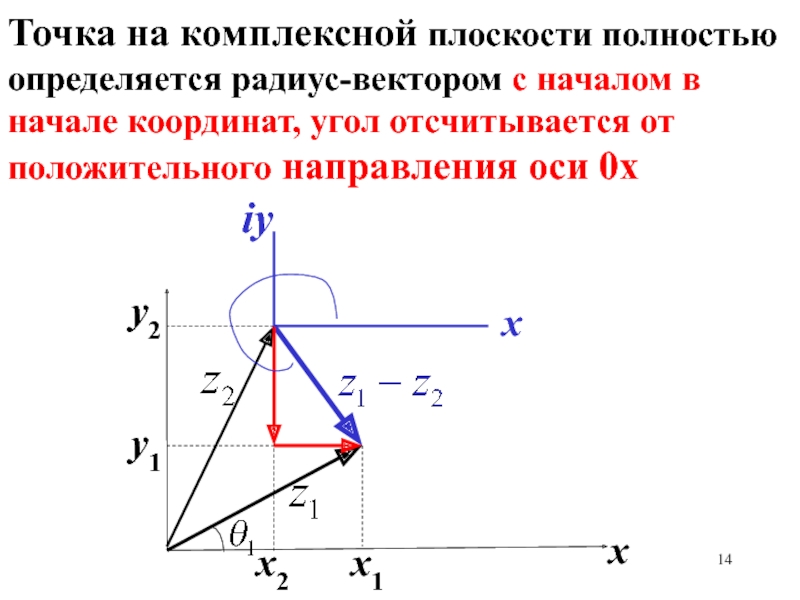
– аргумент числа (z – ak)Слайд 14Точка на комплексной плоскости полностью определяется радиус-вектором с началом в
начале координат, угол отсчитывается от положительного направления оси 0х
х
х1
х2
у1
у2
х
iy
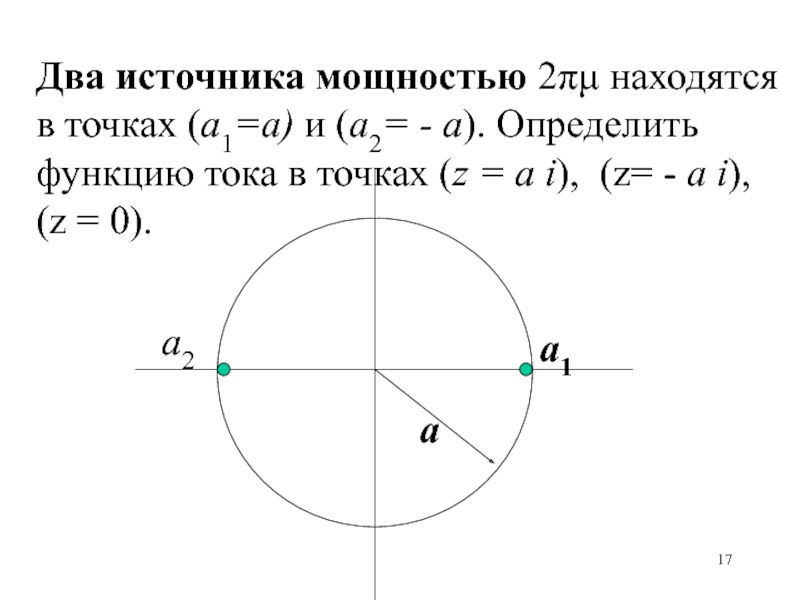
Слайд 17a
Два источника мощностью 2 находятся в точках (а1=а) и (а2=
- а). Определить функцию тока в точках (z = а
i), (z= - а i), (z = 0).a1
a2
Слайд 25Два источника мощностью 2 находятся в точках (а1=а+i) и (а2=
- а+i).
a1
a2
Найти комплексный потенциал и комплексную скорость в точке z
= (1,0)Слайд 27Определить поток скорости и ротор скорости по окружности радиуса R,
в центре которой помещен сток мощностью μ
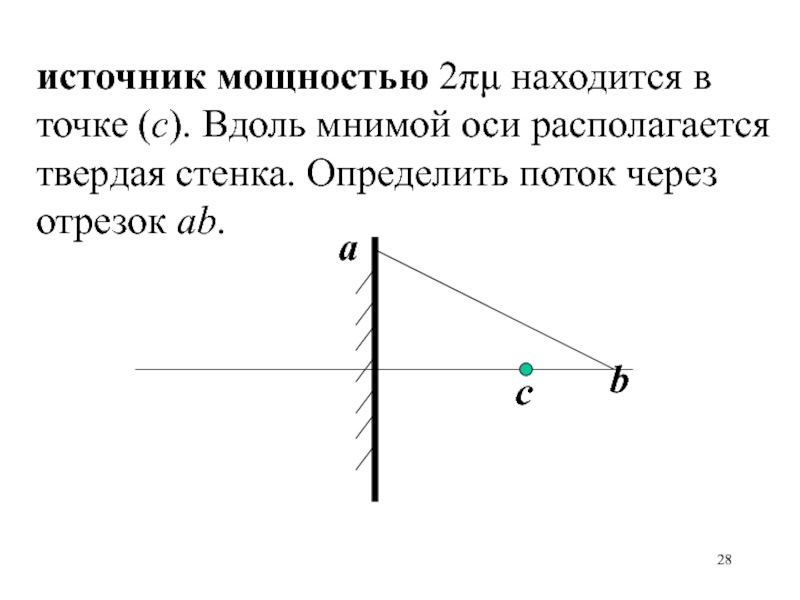
Слайд 28с
источник мощностью 2 находится в точке (с). Вдоль мнимой оси
располагается твердая стенка. Определить поток через отрезок ab.
a
b
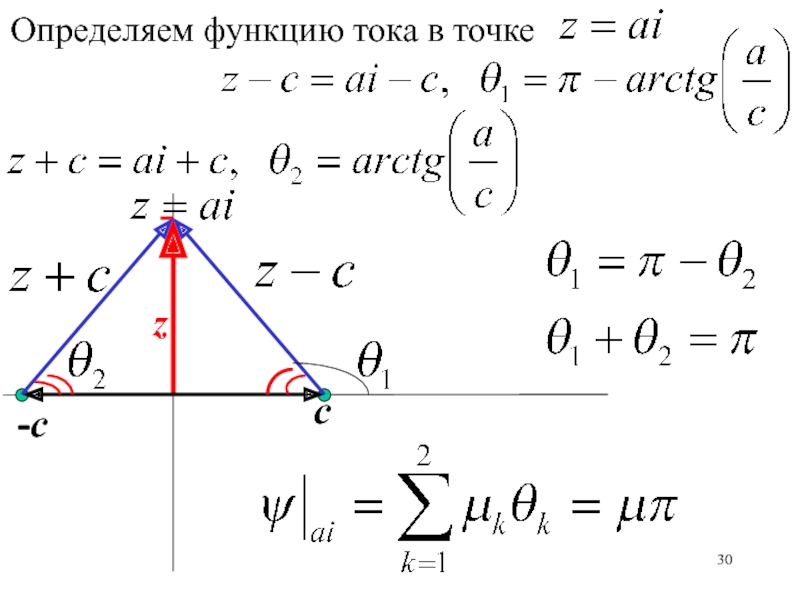
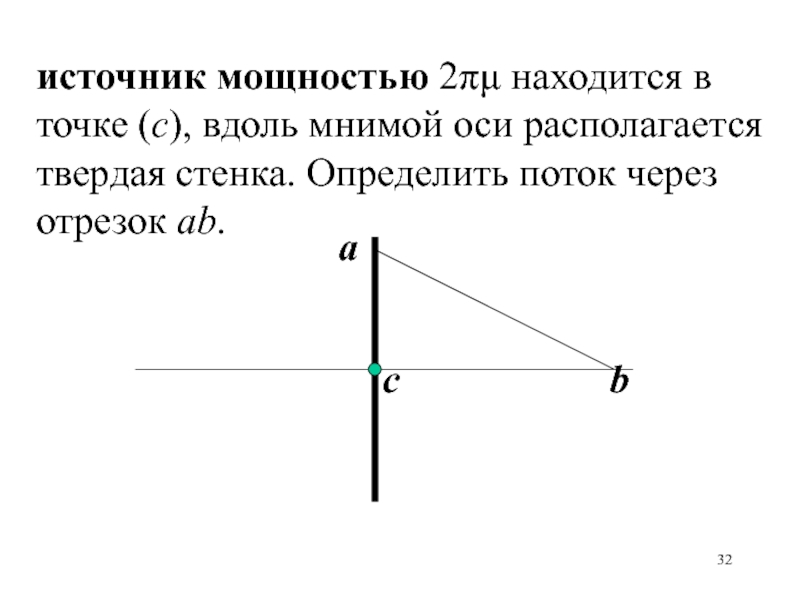
Слайд 32с
источник мощностью 2 находится в точке (с), вдоль мнимой оси
располагается твердая стенка. Определить поток через отрезок ab.
a
b
Слайд 35В начале координат помещен источник интенсивности 2 , вдоль оси
х и оси у установлены стенки, образующие прямой угол. Определить
поток через отрезок [z1=(1,0) z2=(0,i)]. Определить комлексные потенциал и скорость в точке z1=(1,0).Слайд 39В точке z=1+i имеeтся источник интенсивности 2 , а в
начале координат сток интенсивности -2 . Вдоль оси х и
вдоль оси у установлены стенки, образующие прямой угол.Определить комплексный потенциал, линии тока и скорость в точке z=1.
Слайд 52Потенциал скорости - неоднозначная функция координат на плоскости ОХУ .
При обходе вокруг начала координат величина потенциала меняется на
.=const
=0
= - 2
Слайд 54Скорость:
Циркуляция скорости по замкнутому контуру L:
Циркуляцию скорости назовем интенсивностью вихревой
точки
r
d
L
Слайд 55Вихревая точка, расположенная в начале координат z = 0 создает
плоское движение, определяемое комплексным потенциалом
Слайд 57Если вихревая точка не в начале координат, а в точке
z = a, то
Для n точек с интенсивностями 1,…, n
Слайд 581
-1
i
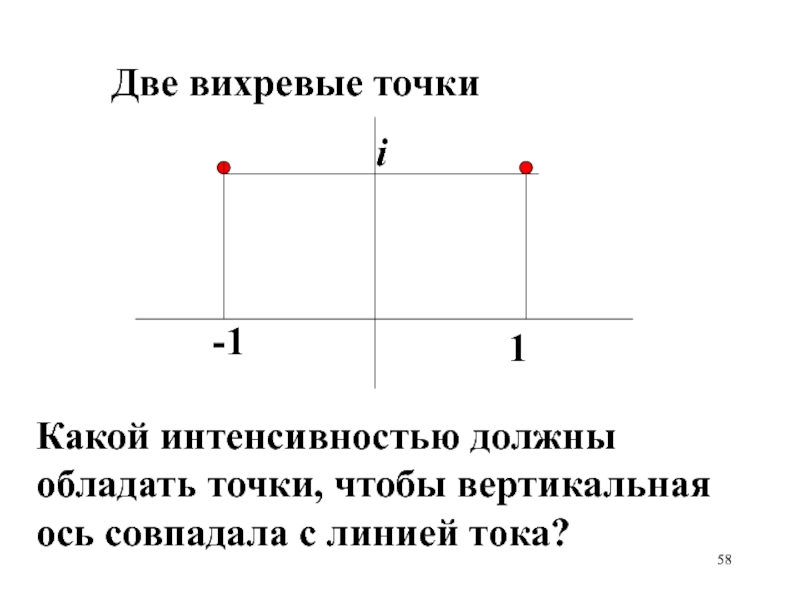
Две вихревые точки
Какой интенсивностью должны обладать точки, чтобы вертикальная ось
совпадала с линией тока?
Слайд 631
-1
i
Две вихревые точки равны по модулю, знак противоположный
вертикальная ось совпадает
с линией тока, если вихревые точки расположены симметрично относительно мнимой
осиСлайд 64Исследовать течение жидкости, которое описывается комплексным потенциалом
a,
b - вещественныеПотенциал скорости, функция тока, комплексная скорость, линии тока
Слайд 65
Начало координат представляет собой особенность - совокупность вихревой точки интенсивности
и источника мощностью m =(2)
Вихреисточник
Слайд 69Структура аналитической функции w(z) вполне определяется распределением на плоскости z
особых точек функции и их характером.
Теория вычетов позволяет выразить циркуляцию
и поток скорости по любому контуру, если для комплексной скоростиизвестны распределения простых полюсов и им соответствующие вычеты
Слайд 70Если простые полюсы функции U*
лежат в точках z=a1, z=a2,…z=an и
вычеты им соответствующие есть А1, А2,…Аn, то линейный интеграл от
функции U* по замкнутому контуру L , заключающему полюсы в точках z=a1, z=a2,…z=an , даетСлайд 81Пусть малое расстояние между источником и стоком будет обозначено s
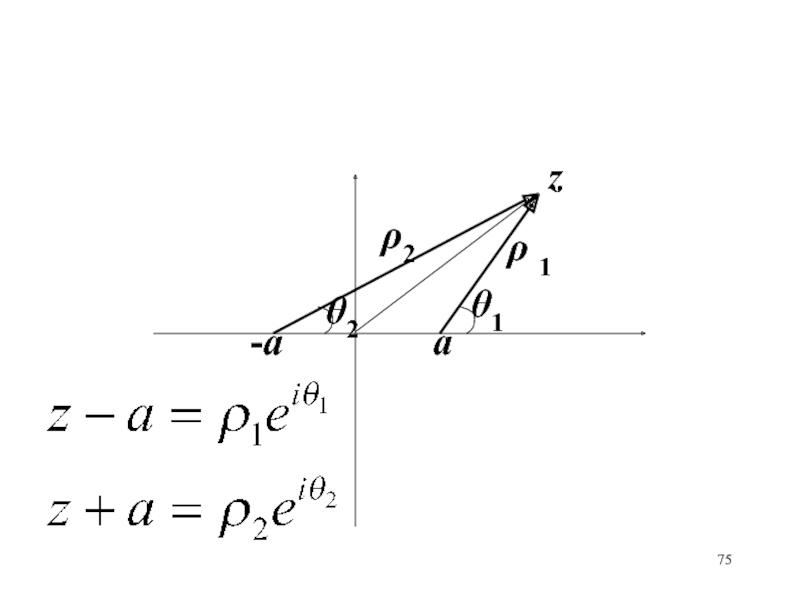
z
r1
r2
1
2
s
С
точностью до малых величин второго порядка малости
Слайд 82Разлагаем в ряд
При s 0 получаем для потенциала скорости
Для сопряженной
функции тока по формуле
Ответ
Записать комплексный потенциал
Слайд 83Для комплексного потенциала получаем
Если ось дублета s составляет угол
с 0х
Записать потенциал скорости и функцию тока
Слайд 84Если на плоскости 0ху в точках z = an помещены
дублеты моменты которых равны Mn , а оси дублетов составляет
угол n с вещественной осью 0х, то комплексный потенциал определяется:Слайд 85Дублет находится в точке z = a, где а >
0, вещественное. Определить поток жидкости через отрезок [z = 0,
z = i]Определить горизонтальную составляющу скорости в точке z = i
а
i
Слайд 88Определить поток жидкости через отрезок [-a+i, a+i]
Какое течение определяет комплексный
потенциал?
Слайд 91Исследовать течение жидкости (плоское, безвихревое), которое описывается потенциалом скорости
, с > 0 - вещественное
Контрольная работа
Какой объем жидкости протекает в единицу времени через отрезок z2 z1 [z1=0, z2=1+i]?
Указать 2 линии тока
Слайд 96ЗАДАЧА 1
Найти линии тока, получить проекции скорости, посчитать поток через
отрезок [z = 0, z = 1+31/2i]
Слайд 100Найти функцию тока. В каких точках находятся источники и стоки?
Найти уравнение линий тока. Показать, что линиями тока являются оси
координат и окружность r = 1.Какой объем жидкости протекает в единицу времени через отрезок [z1=i, z2=1/2]?
ЗАДАЧА 2
Слайд 103Какой системой надо заменить источник между двух стенок для того,
чтобы написать комплексный потенциал?
х
y
Слайд 105Эти же формулы имеют место для источника, помещенного на одинаковом
расстоянии от двух параллельных твердых стенок, имеющих координаты
Слайд 108Задача
Течение определяется потенциалом
Найти поток жидкости через окружность
И циркуляцию скорости по
этой окружности
Слайд 116Мощность источника 2
Поток массы (мощность источника), проходящий через окружность радиуса
r в единицу времени, определяется произведением радиальной скорости на длину
окружностине зависит от радиуса (сохранение массы). Если <0, то определяет сток.



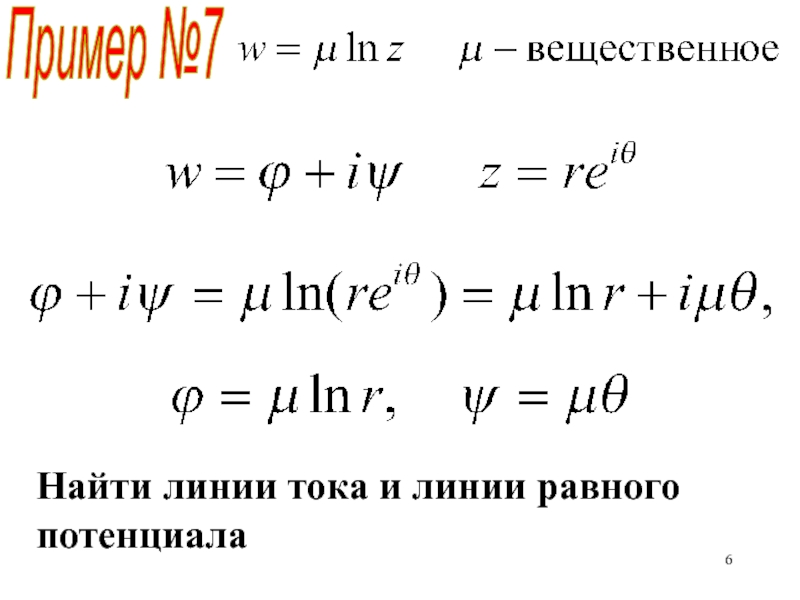




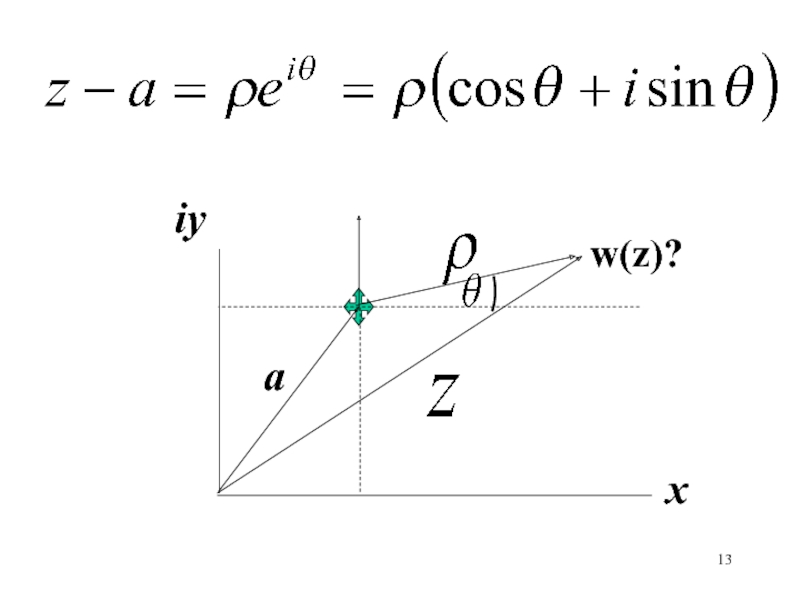
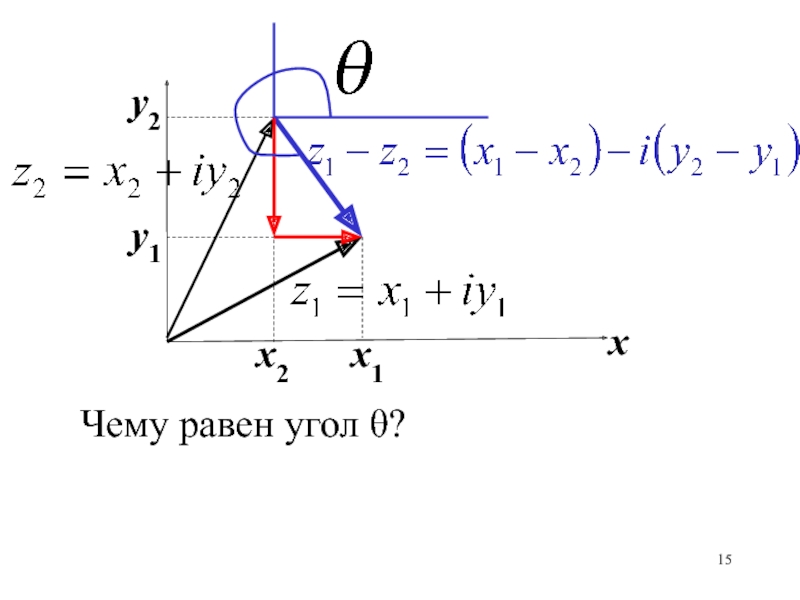
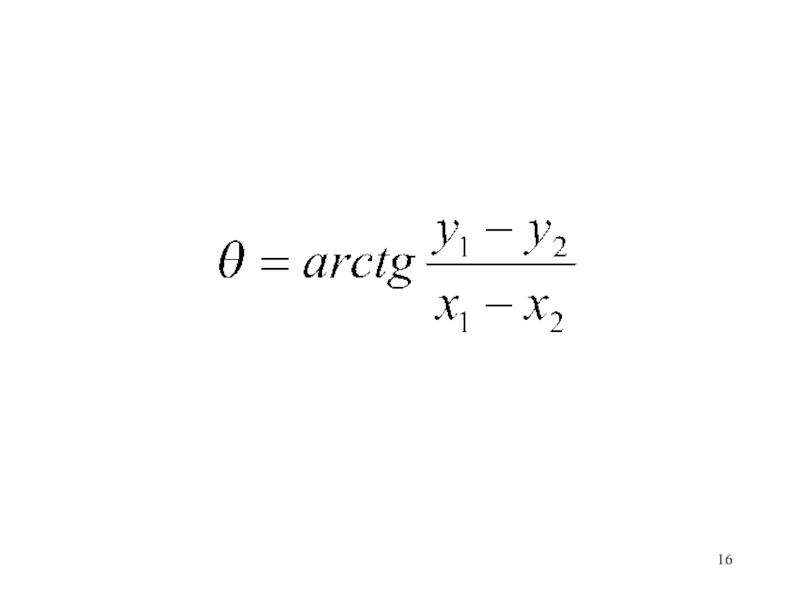
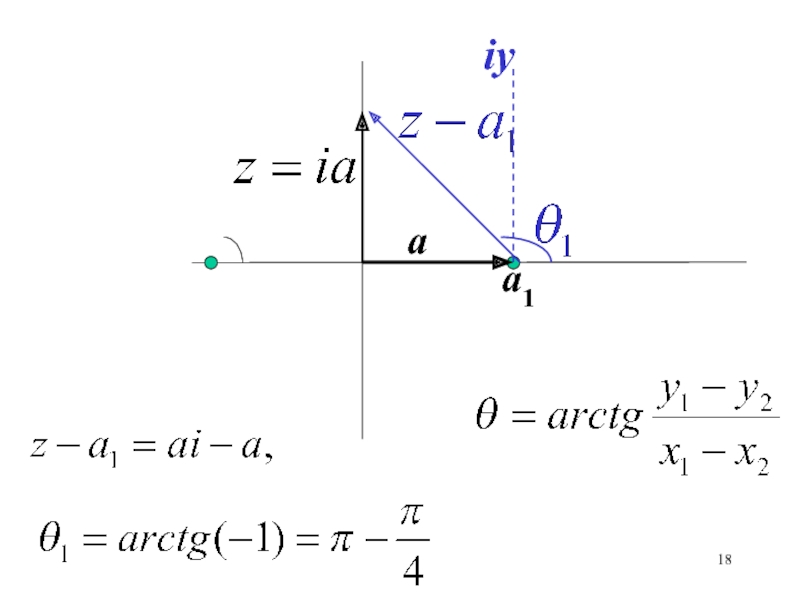
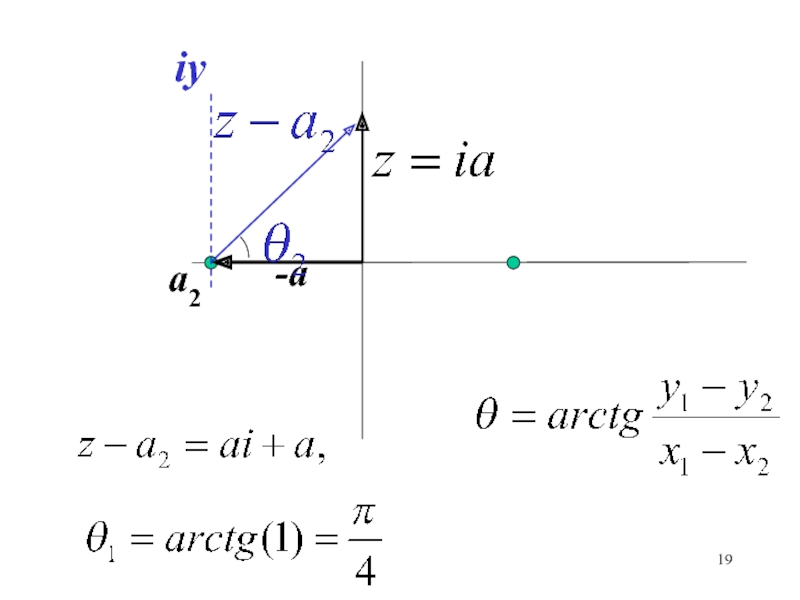
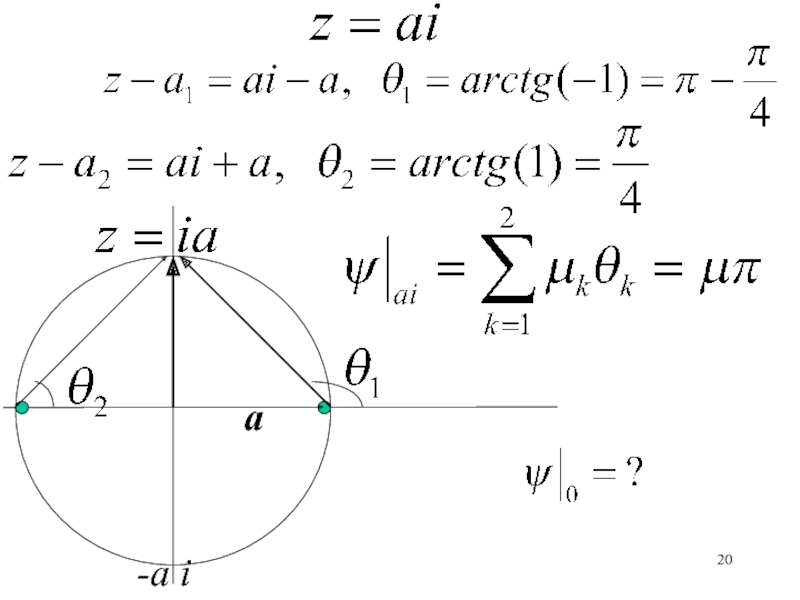
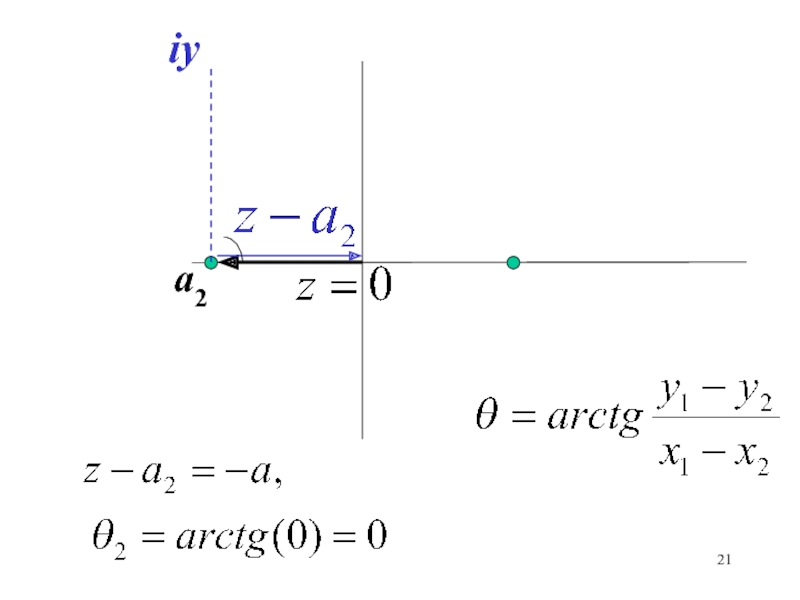
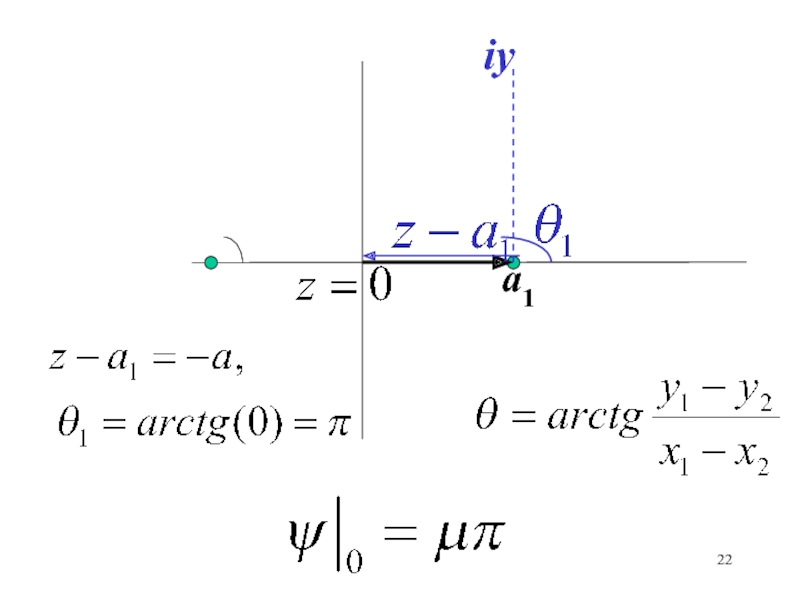
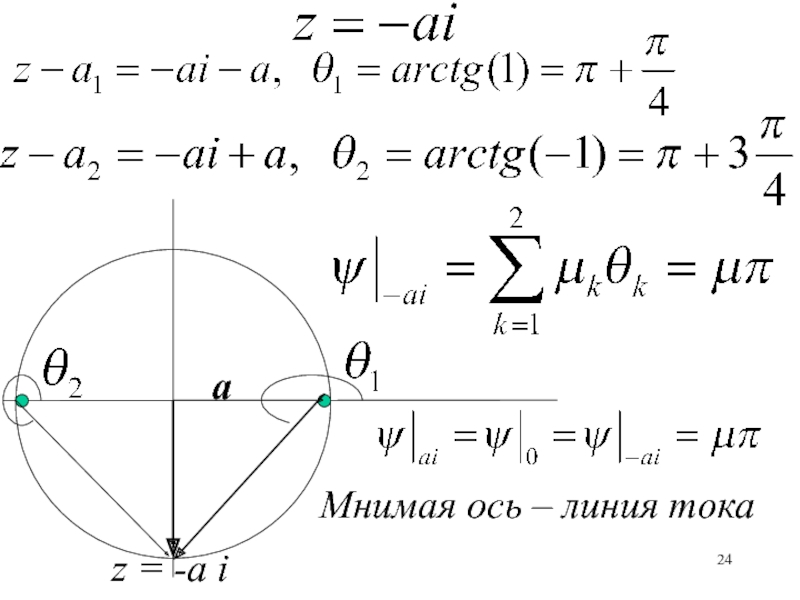

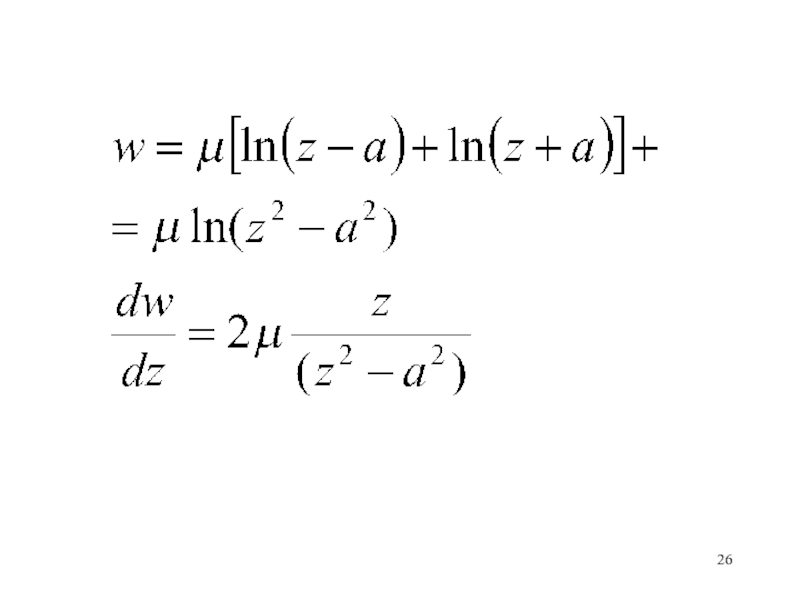




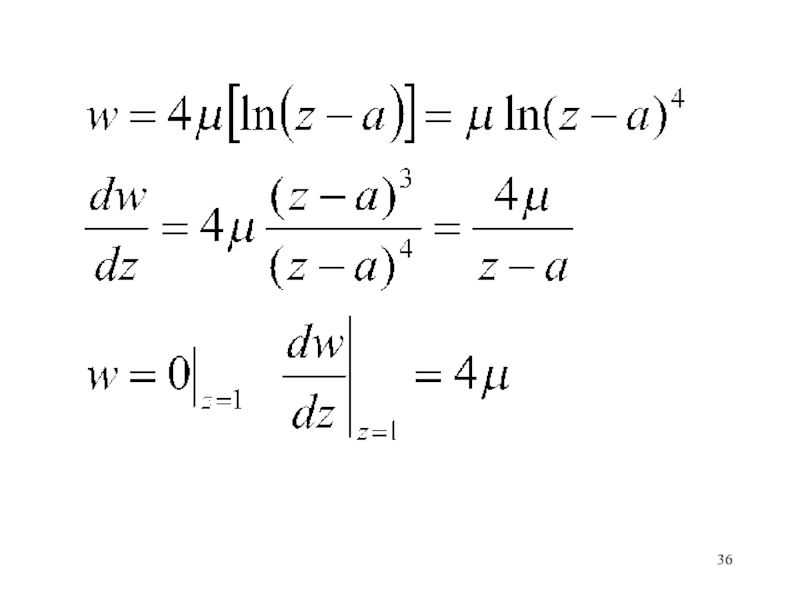

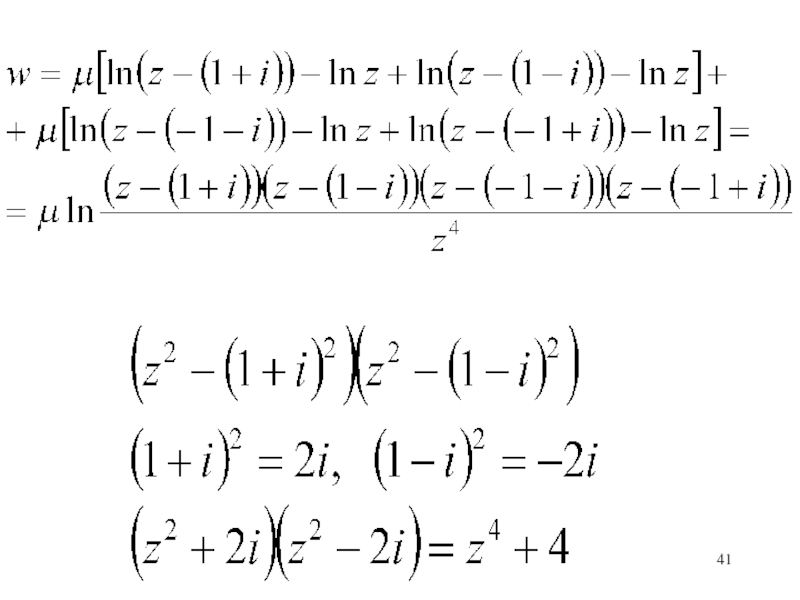
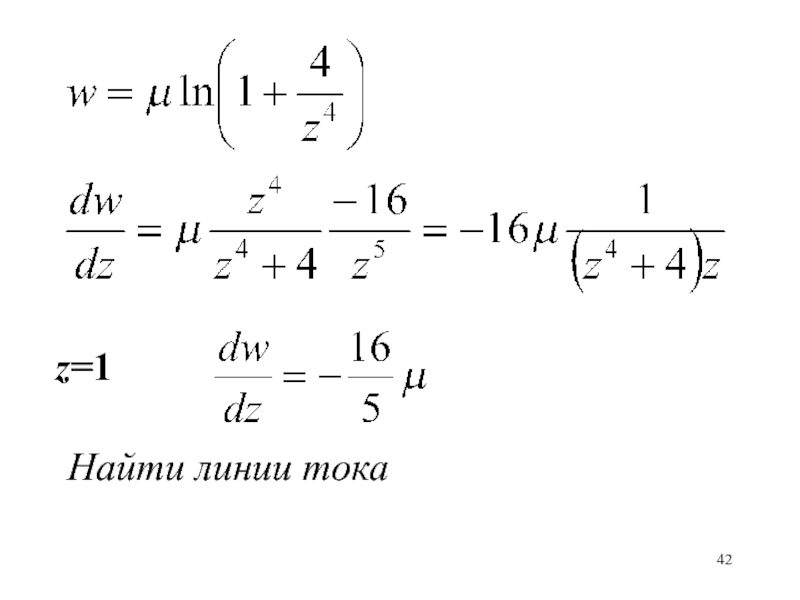
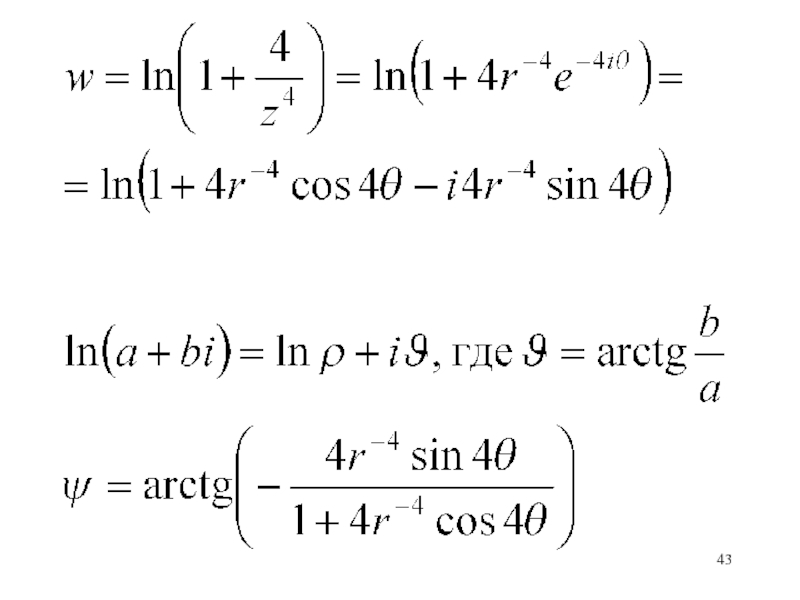



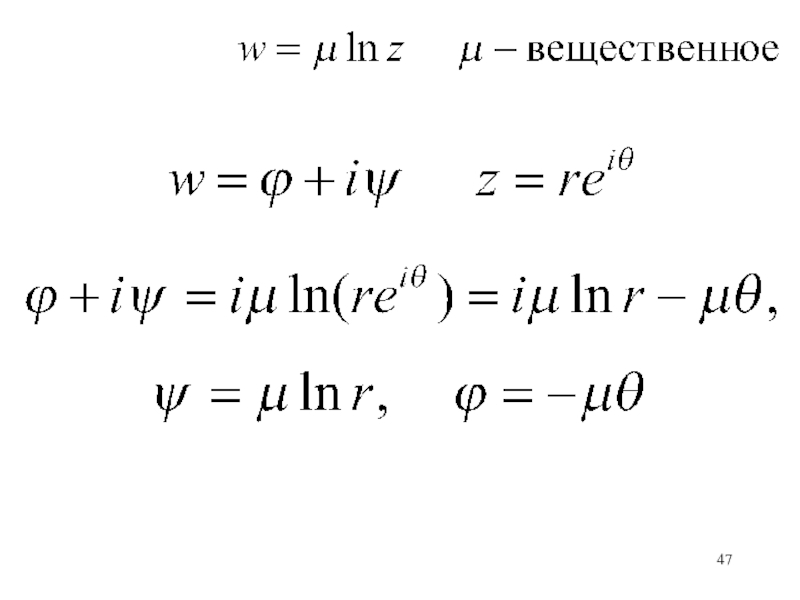









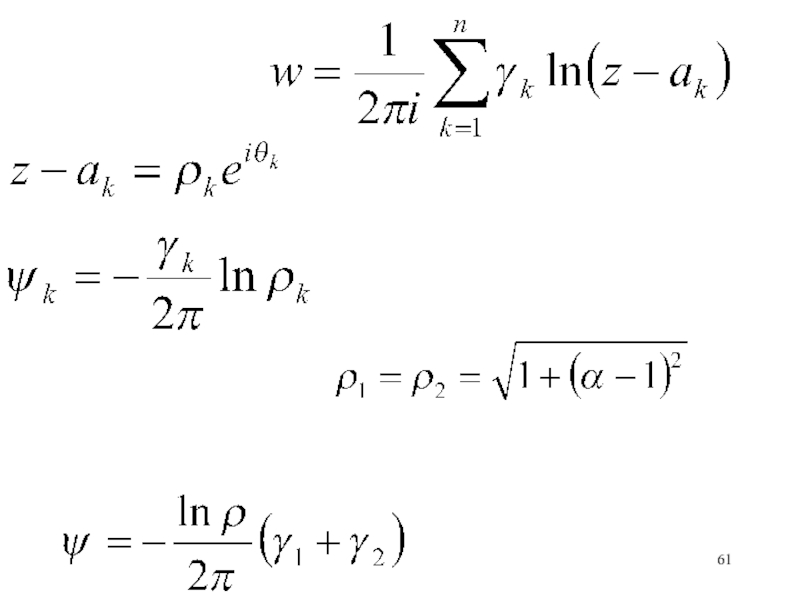
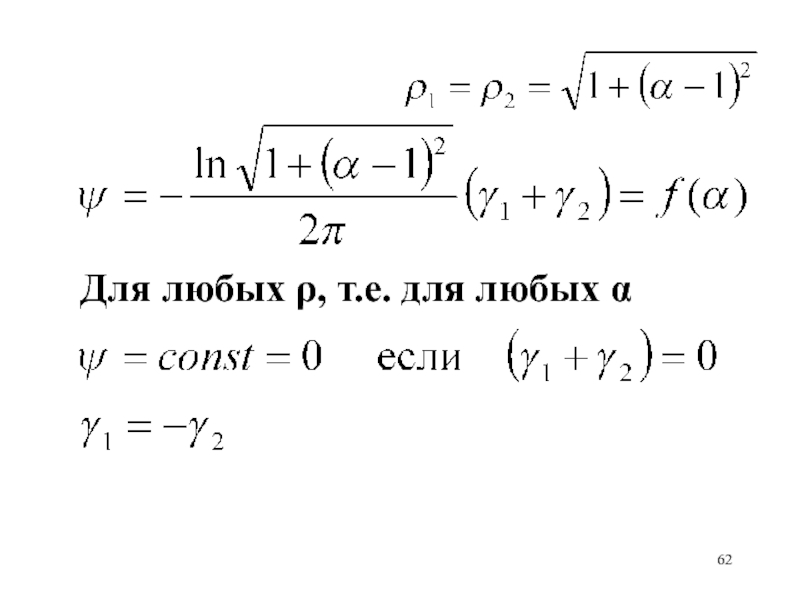


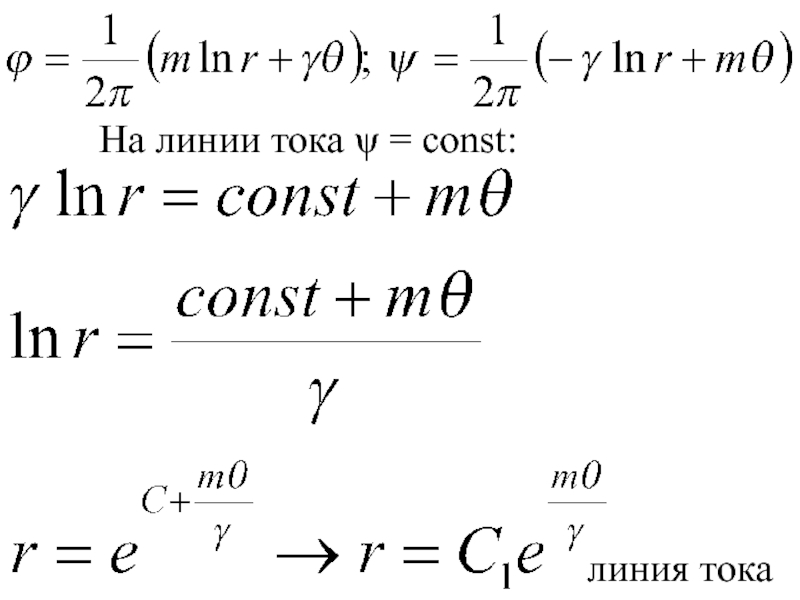






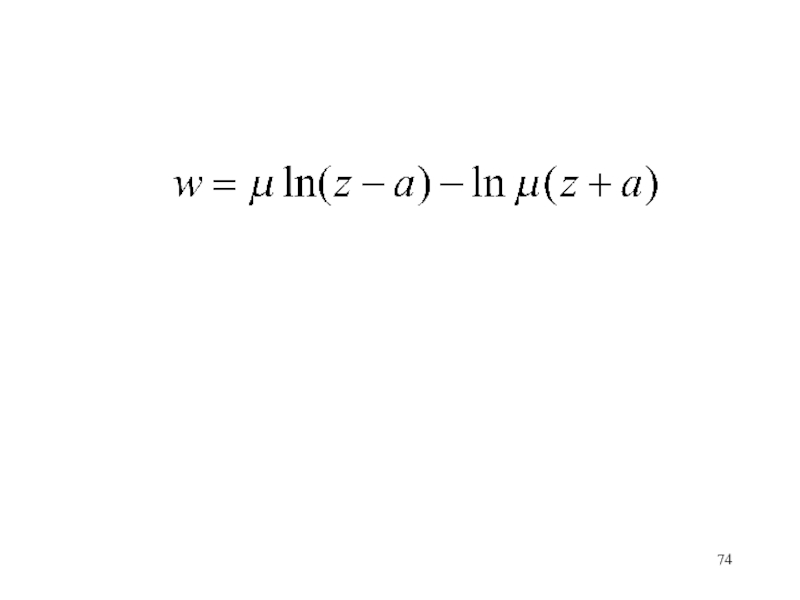
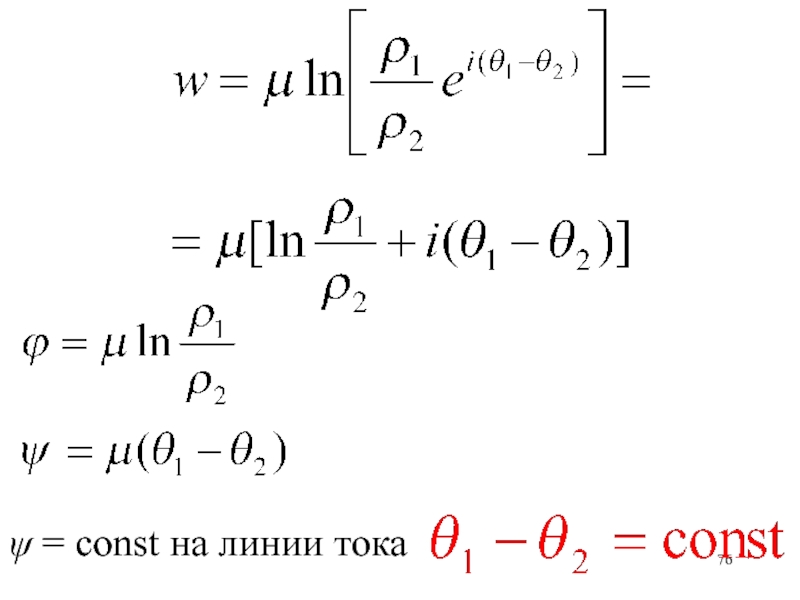






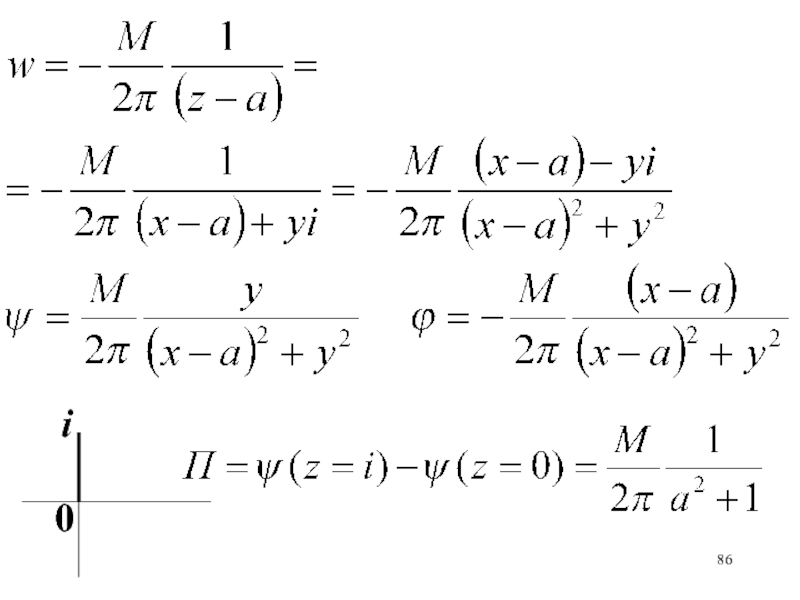
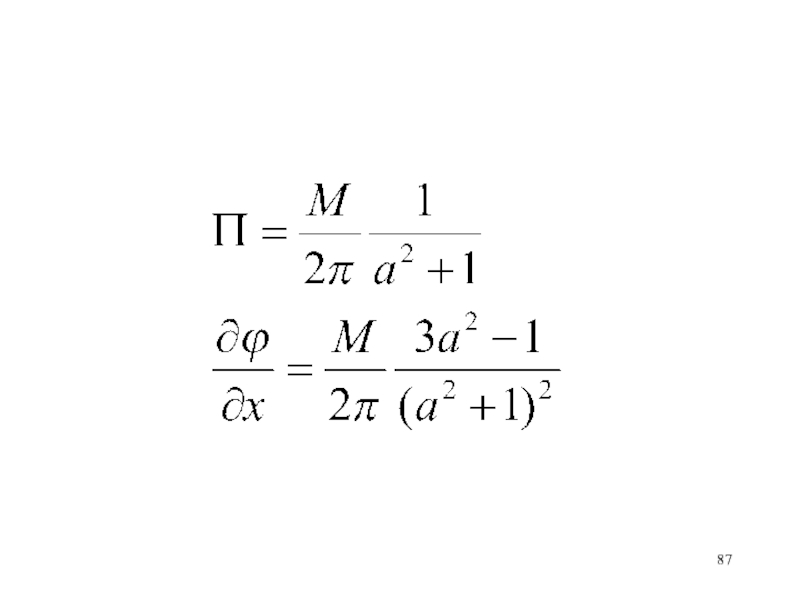
![1
Эйлер, Ляпунов, Навье и Стокс Определить поток жидкости через отрезок [-a+i, a+i]Какое течение определяет комплексный потенциал? Определить поток жидкости через отрезок [-a+i, a+i]Какое течение определяет комплексный потенциал?](/img/thumbs/52251ed6ca51170a1b63dee993ebede1-800x.jpg)


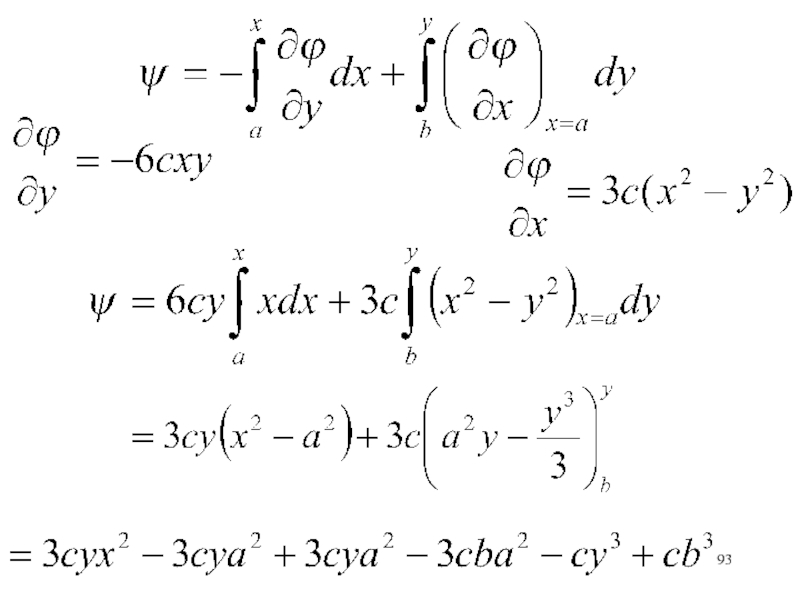
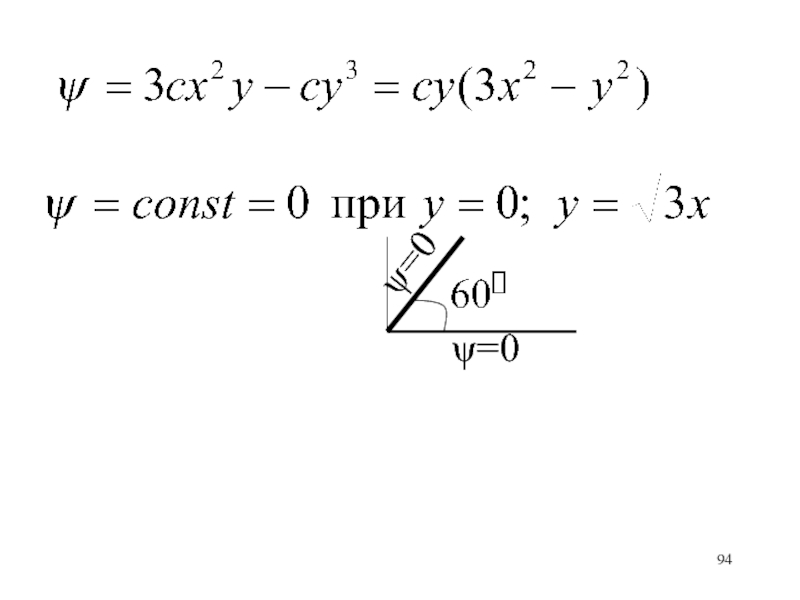
![1
Эйлер, Ляпунов, Навье и Стокс [z1=0, z2=1+i]11хуz1z2 [z1=0, z2=1+i]11хуz1z2](/img/thumbs/cd8a0b12734678977642083f57a2f0fc-800x.jpg)
![1
Эйлер, Ляпунов, Навье и Стокс ЗАДАЧА 1Найти линии тока, получить проекции скорости, посчитать поток через отрезок ЗАДАЧА 1Найти линии тока, получить проекции скорости, посчитать поток через отрезок [z = 0, z = 1+31/2i]](/img/thumbs/0860ca2241f052c050521887e6aa8084-800x.jpg)