Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Логарифмические уравнения
Содержание
- 1. 1 Логарифмические уравнения
- 2. Свойства логарифма
- 3. Слайд 3
- 4. Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими уравнениями.
- 5. Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:
- 6. Основные методы решения логарифмических уравнений По определению
- 7. Слайд 7
- 8. Методы решения логарифмических уравненийПо определению логарифма.На основе
- 9. 2. Метод потенцирования.Под потенцированием понимается переход от
- 10. 13. Метод введения новой переменнойlog22x – 4log2
- 11. 4. Метод логарифмированияx0,5lgx=0,01x2 Прологарифмируем обе части уравнения
- 12. 5. Метод приведения логарифмов к одному и
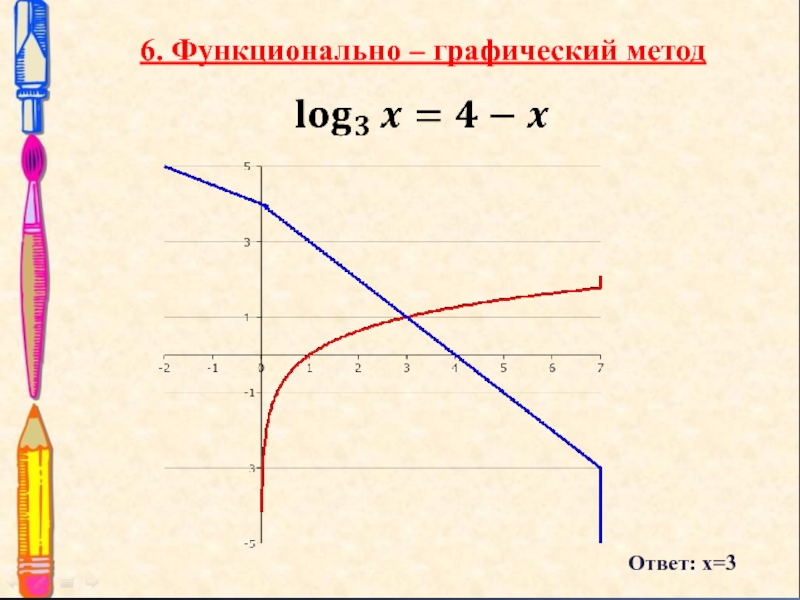
- 13. 6. Функционально – графический методОтвет: х=3
- 14. Для решения ЛУ графическим методом надо построить
- 15. 7. Использование свойств монотонности функции log3 x
- 16. Самостоятельная работа (в парах)Укажите метод и решите уравнения:Ответы (самопроверка)150,25; 162; -40, 125; 25125; 0,04-43; 27
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма
называются логарифмическими уравнениями.
Слайд 5Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих
теоремах:
Слайд 6Основные методы решения логарифмических уравнений
По определению логарифма;
Метод потенцирования;
Метод введения
новой переменной;
Метод логарифмирования;
Метод приведения к одному основанию;
Функционально-графический метод.
Слайд 8Методы решения логарифмических уравнений
По определению логарифма.
На основе определения логарифма решаются
уравнения, в которых по данным основанию и числу определяются логарифм,
по данному логарифму и основанию определяется число и по данному числу и логарифму определяется основание.X=2,5
Слайд 92. Метод потенцирования.
Под потенцированием понимается переход от равенства, содержащего логарифмы
к равенству, не содержащего их.
f(x) = y(x)
Условия для проверки всегда
составляем по исходящему уравнению !при
Слайд 101
3. Метод введения новой переменной
log22x – 4log2 x + 3=0
log2
x= t, x>0
t2 – 4t + 3=0
t1=3
t2=1log2 x=1 log2 x=3
x=2
x=8
Ответ: x=2; 8
Слайд 114. Метод логарифмирования
x0,5lgx=0,01x2
Прологарифмируем обе части уравнения по основанию 10
lg
x 0,5lgx=lg 0,01x2
0,5 lg2x – 2lg x + 2 =
0t2 – 4t + 4 = 0
t=lg x
0,5t2 – 2t - 2 = 0
(t-2)2 = 0
t = 2 lg x = 2
Ответ: x=100
Слайд 125. Метод приведения логарифмов к одному и тому же основанию
log9
(37 – 12x) * log7-2x 3 = 1
ОДЗ
0,5log3 (37 -
12x) = log3 (7 – 2x)log3 (37 - 12x) = log3 (7 – 2x)2
37 – 12x = (7 – 2x)2
37 – 12x = 49 -28x + 4x2
X2 – 4x + 3 = 0
x1 = 1
x2 = 3 – посторонний корень
Ответ: х = 1
Слайд 14Для решения ЛУ графическим методом надо построить в одной и
той же системе координат графики функций, стоящих в левой и
правой частях уравнения и найти абсциссу их точки пересечения Найти корни уравнения
Так как функция у= log3 х возрастающая, а функция у =4-х убывающая на (0; + ∞ ),то заданное уравнение на этом интервале имеет один корень.
Слайд 157. Использование свойств монотонности функции
log3 x = 11 –
x
Так как функции y = log3 x возрастает, а у
= 11 – x убывает на (0;+∞),то уравнение имеет единственное решение, которое можно найти методом подбора: х = 9