Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Циклические вычислительные процессы Циклы накопления суммы ( произведения
Содержание
- 1. 1 Циклические вычислительные процессы Циклы накопления суммы ( произведения
- 2. Вычисление суммы заключается в ее накоплении, т.е.
- 3. 1. Вычисляем первое слагаемое и добавляем его
- 4. Начальное значение суммы: S = 0
- 5. Формула для накопления суммы (общая формула):S = S + yтекущее значение суммыпредыдущее значение суммытекущее слагаемое
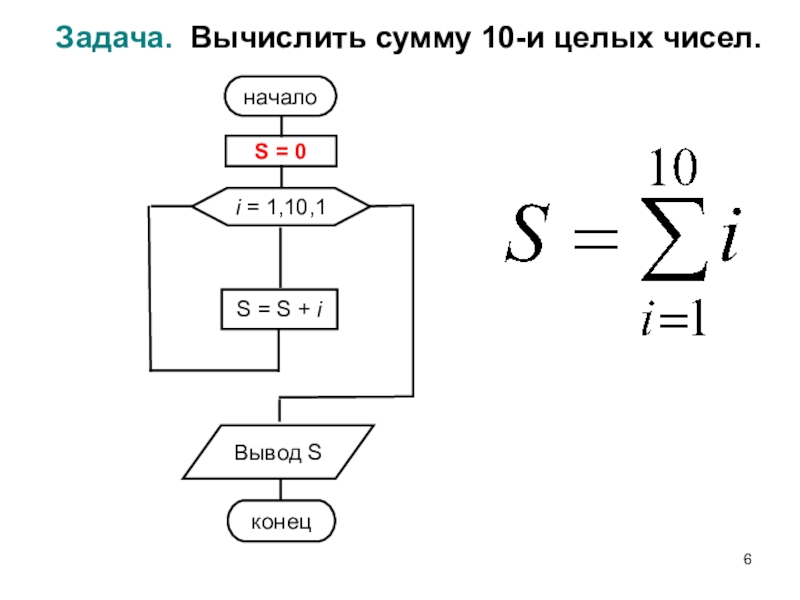
- 6. Задача. Вычислить сумму 10-и целых чисел. началоi = 1,10,1S = S + iВывод SконецS = 0
- 7. Программный код:{double s=0; for (int i=1; i
- 8. Цикл накопления суммыПример. Вычислитьобщий вид слагаемого (формульный вид)сумма каждого слагаемогообщая формула:
- 9. Цикл накопления суммы Пример. Вычислить
- 10. Аналогично вычисляется произведение.Формула для накопления произведения(общая формула):P
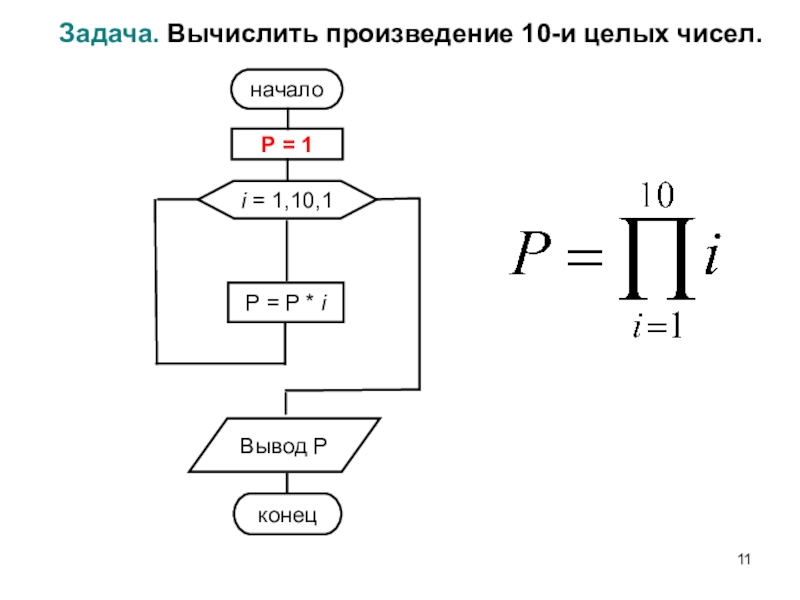
- 11. Задача. Вычислить произведение 10-и целых чисел. началоi = 1,10,1P = P * iВывод PконецP = 1
- 12. Задача. Найти факториал числа N.Факториал числа определяется
- 13. Цикл накопления произведенияПример. Вычислить
- 14. Цикл накопления произведения Пример.
- 15. Цикл накопления суммы (произведения)Пример. Вычислитьпри u=0,5
- 16. q = 29; 43; 1 3p =
- 17. Вычисление суммы рядаЧисловой знакопеременный ряд: Пронумеруем
- 18. Задача. Вычислить сумму первых N членов ряда.
- 19. Вычисление суммы рядаПример. Вычислитьy =110 – (cos3x
- 20. i = 3; 21; 2 3Конец 8Вывод
- 21. Итерационные циклыИтерационный цикл – цикл последовательных приближений
- 22. Выходом из этого цикла является выполнение условия,
- 23. Рассмотрим несколько шагов цикла: (где n
- 24. НачалоНет{ double x, e; cin>>x>>e;
- 25. Скачать презентанцию
Вычисление суммы заключается в ее накоплении, т.е. основано на использовании предыдущих вычисленных значений слагаемых.Рационально при накоплении значений использовать циклический алгоритм.
Слайды и текст этой презентации
Слайд 2Вычисление суммы заключается в ее накоплении, т.е. основано на использовании
предыдущих вычисленных значений слагаемых.
Слайд 31. Вычисляем первое слагаемое и добавляем его к начальному значению
S.
2. Вычисляем очередное слагаемое и добавляем его к сумме
предыдущих слагаемых. Таким образом в цикле вычисляются все промежуточные суммы.
Математическая запись:
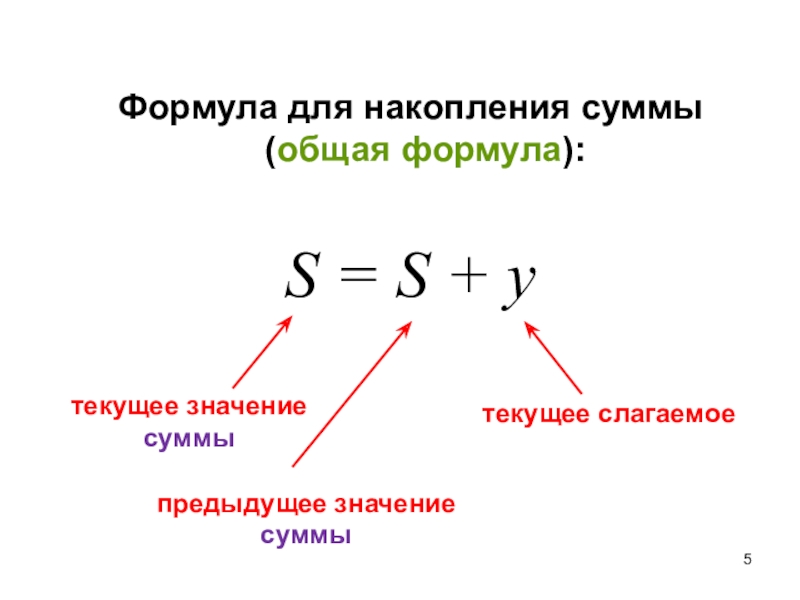
Слайд 5Формула для накопления суммы (общая формула):
S = S + y
текущее
значение суммы
предыдущее значение суммы
текущее слагаемое
Слайд 7Программный код:
{
double s=0;
for (int i=1; i
{
s=s+i; // s+=i}
cout<
return 0;
}
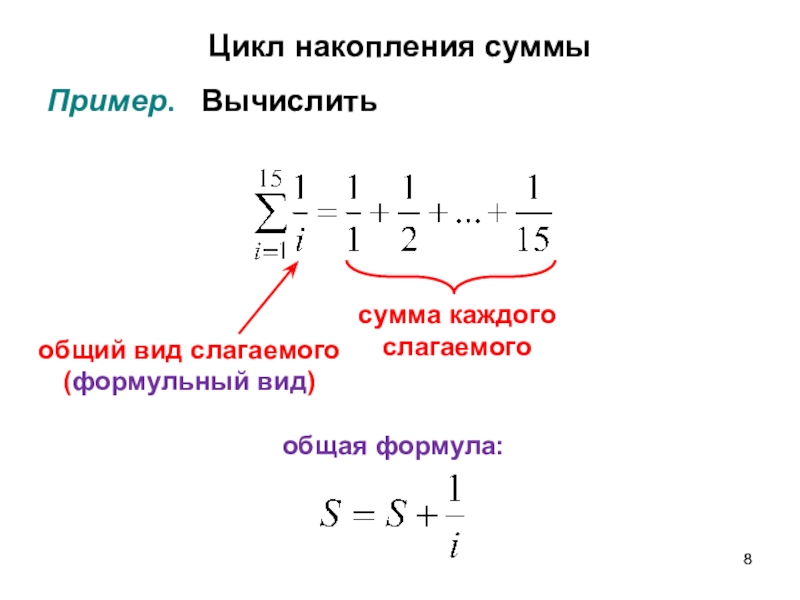
Слайд 8Цикл накопления суммы
Пример. Вычислить
общий вид слагаемого (формульный вид)
сумма каждого
слагаемого
общая формула:
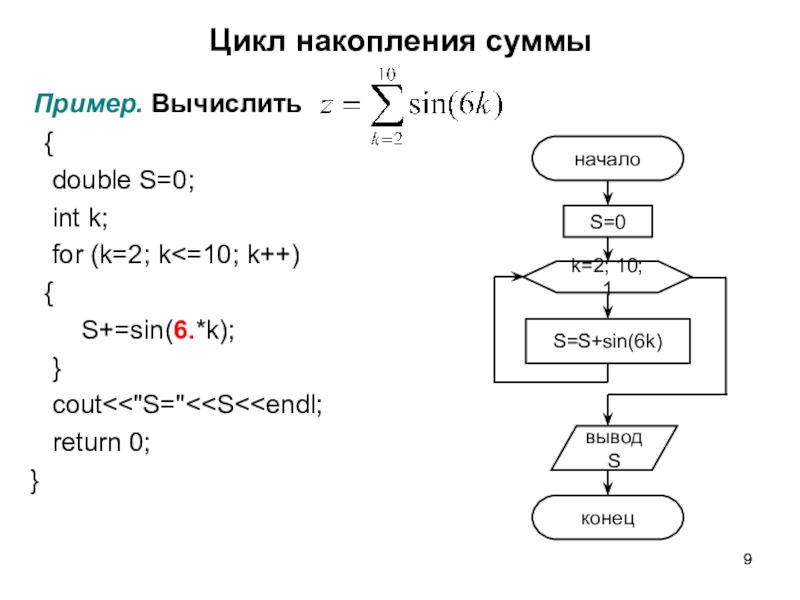
Слайд 9Цикл накопления суммы
Пример. Вычислить
{
double S=0;
int k;
for
(k=2; k<=10; k++){
S+=sin(6.*k);
}
cout<<"S="<
}
начало
S=0
k=2; 10; 1
S=S+sin(6k)
вывод S
конец
Слайд 10Аналогично вычисляется произведение.
Формула для накопления произведения
(общая формула):
P = P *
y
Начальное значение произведения должно быть отлично от нуля.
Например, равно
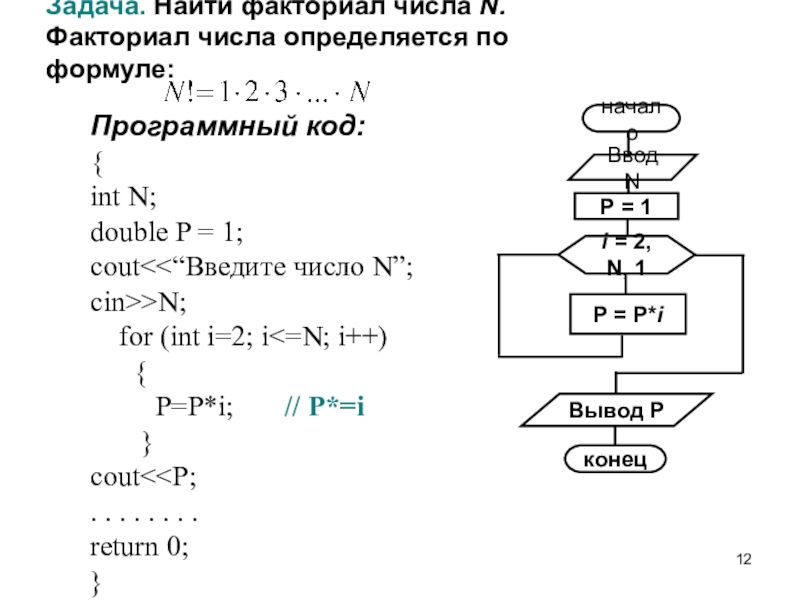
единице.
Слайд 12Задача. Найти факториал числа N.
Факториал числа определяется по формуле:
Программный код:
{
int N;
double P = 1;
coutN;
for
(int i=2; i<=N; i++){
P=P*i; // P*=i
}
cout<
return 0;
}
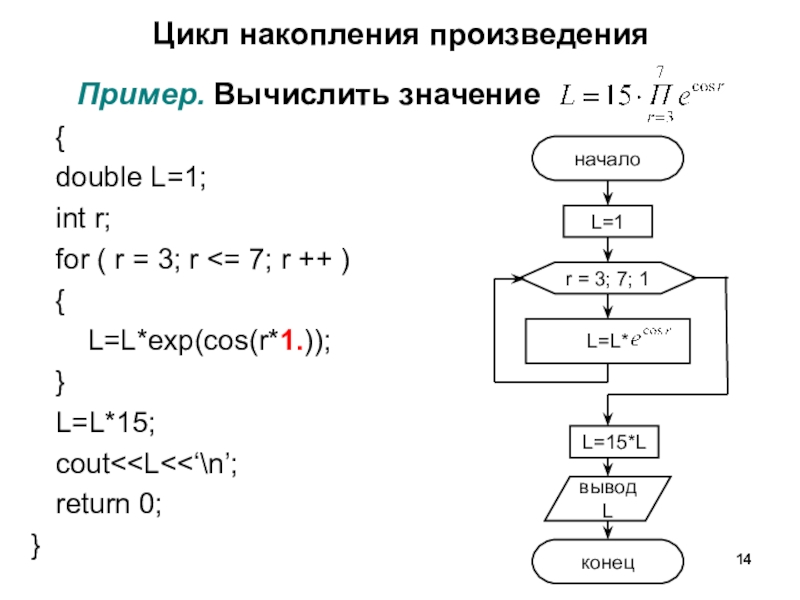
Слайд 14Цикл накопления произведения
Пример. Вычислить значение
{
double L=1;
int r;
for ( r = 3; r <= 7; r ++ ){
L=L*exp(cos(r*1.));
}
L=L*15;
cout<
}
начало
L=1
r = 3; 7; 1
L=L*
вывод L
конец
L=15*L
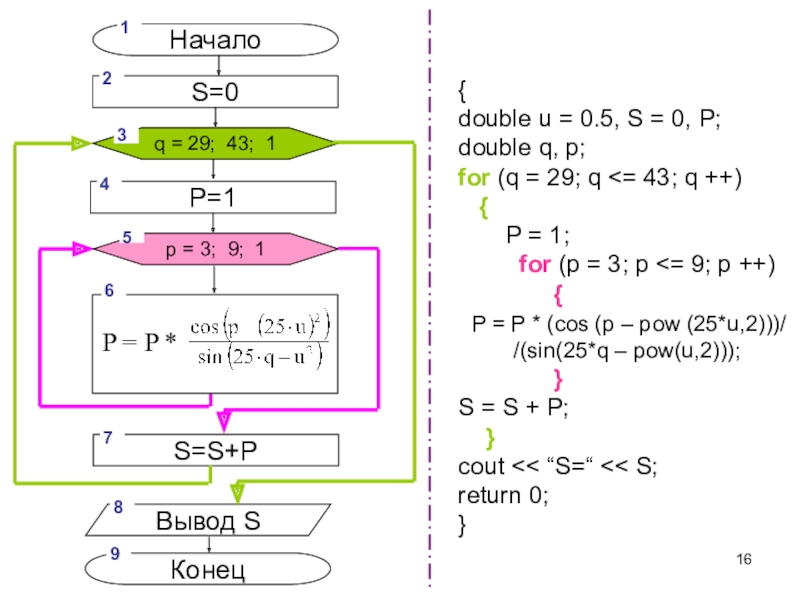
Слайд 16q = 29; 43; 1
3
p = 3; 9; 1
5
{
double u = 0.5, S = 0, P;
double q, p;
for
(q = 29; q <= 43; q ++){
P = 1;
for (p = 3; p <= 9; p ++)
{
P = P * (cos (p – pow (25*u,2)))/
/(sin(25*q – pow(u,2)));
}
S = S + P;
}
cout << “S=“ << S;
return 0;
}
Слайд 17Вычисление суммы ряда
Числовой знакопеременный ряд:
Пронумеруем члены этого ряда:
i = 1 2 3 4 …
Найдем формулу, по которой
можно определить любой член ряда в зависимости от его порядкового номера:где Ai – член ряда.
Сумма накапливается по формуле S = S + A,
где А – очередное слагаемое.
Слайд 18Задача. Вычислить сумму первых N членов ряда.
double a, s
= 0; / начальное значение суммы
int с = 1, N;cin>>N;
for (int i = 1; i <= N; i ++)
{
a = с * 1 / (i + 1); / вычисление очередного члена ряда
s = s + a; / накопление суммы
с = - с; / смена знака вспомогательной переменной
}
cout <<"Сумма ряда s =" << s;
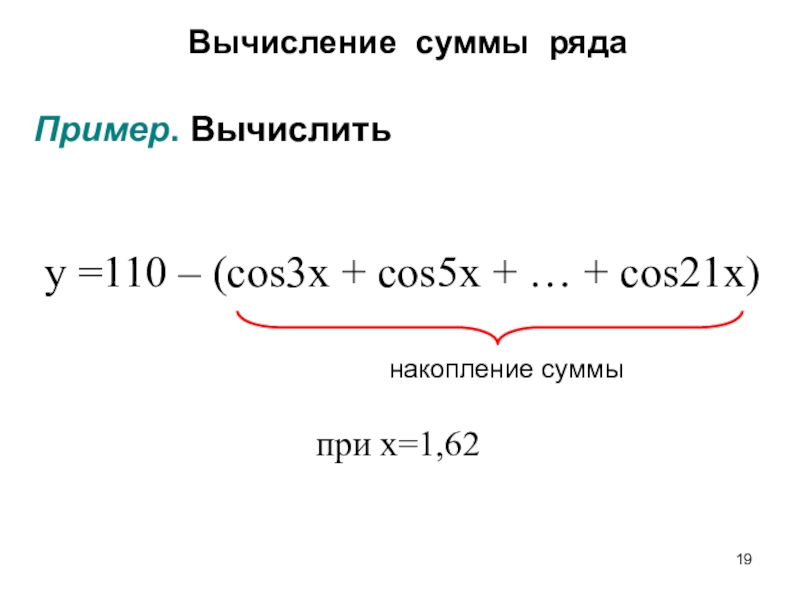
Слайд 19Вычисление суммы ряда
Пример. Вычислить
y =110 – (cos3x + cos5x +
… + cos21x)
накопление суммы
при x=1,62
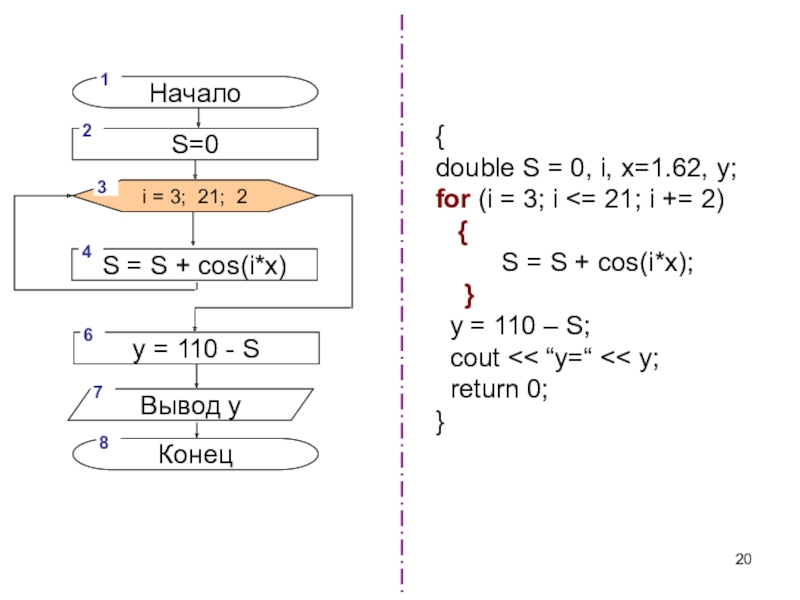
Слайд 20i = 3; 21; 2
3
Конец
8
Вывод y
7
{
double S
= 0, i, x=1.62, y;
for (i = 3; i
21; i += 2){
S = S + cos(i*x);
}
y = 110 – S;
cout << “y=“ << y;
return 0;
}
Слайд 21Итерационные циклы
Итерационный цикл – цикл последовательных приближений к искомому значению
с заданной точностью. Количество повторений данного цикла заранее неизвестно.
Пример. Вычислить
и вывести значения членов бесконечного ряда.с точностью
при х = 0.1
1! = 1
2! = 1*2
3! = 1*2*3 = 2!*3
Слайд 22Выходом из этого цикла является выполнение условия, что значение очередного
члена ряда меньше заданной точности, т.е.
На каждом шаге вычисляется член
ряда и его значение сравнивается со значением .Если сравнить любую пару членов ряда (предыдущий и последующий), то можно отметить свойство – последующий член ряда можно выразить через предыдущий.
Формула, составленная на основе этого свойства, называется рекуррентной.
Слайд 23Рассмотрим несколько шагов цикла:
(где n – номер шага,
А – член ряда)
-- это рекуррентная формула
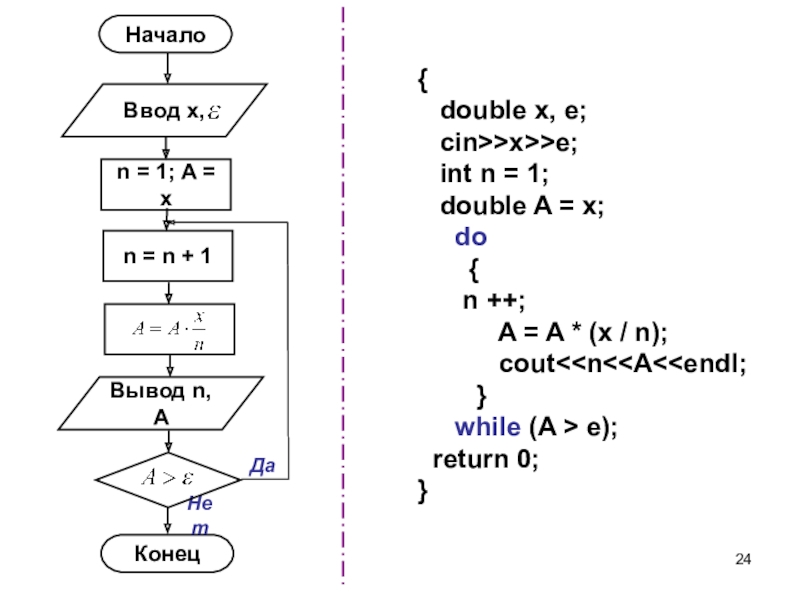
Слайд 24Начало
Нет
{
double x, e;
cin>>x>>e;
int n
= 1;
double A = x;
do
{n ++;
A = A * (x / n);
cout<
while (A > e);
return 0;
}
