1 Ізоморфізм графів Лекція 9 Теорія графів

їх функціонування, що в деяких випадках надає можливість заміни однієї

структури іншою.
Для розпізнавання ізоморфізму графів G = (X, F) і H = (Y, P), що мають n вершин, у загальному випадку необхідно виконати n! попарних порівнянь. Для скорочення обсягу перебору розглянемо алгоритм розпізнавання ізоморфізму графів.
Нехай задано два графи G = (X, F) і H = (Y, P), які мають множини елементів (вершин) X = {xi}, iI та Y = {yj}, jI, де I = {1, 2, ..., n}. Кожному елементу xiX зіставимо пару чисел (si, pi), а елементу yjY – пару (vj, wj), де si і vj – напівстепені виходу, а pi і wj – напівстепені входу кожної вершини, відповідно.

= (X, F) і H = (Y, P) ізоморфні, то

існує підстановка tT, де T – симетрична група підстановок множини елементів, яка визначає бієктивне відображення множини X графа G = (X, Y) у множину Y графа H = (Y, P) таке, що (xiX)(yjY)[(si= vj)(pi = wj)].

від одного тільки впорядкованістю у позначеннях вершин. Але перенумеровання вершин

не змінює напівстепені виходу s і входу p кожної вершини. Тому для будь-якого xiX із парою (si, pi) можна взаємно однозначно визначити таке yjY із парою (vj, wj), що si = vj та pi = wj. Таким чином, знайдено підстановку tT, що переводить граф G = (X, F) у граф H = (Y, P), тобто (xiX)(yjY)[(si = vj)(pi = wj)]. Лему доведено.

Доведення леми 3.1

суміжності A графа G=(X, F) у матрицю суміжності B графа

H = (Y, P), то графи G = (X, F) і H = (Y, P) ізоморфні. Доведення леми випливає із означення ізоморфізму графів.

Лема 3.2 про ізоморфізм графів

граф G = (X, F) був ізоморфним до графа H

= (Y, P), необхідно та достатньо виконання таких умов:
а) (xiX)(yjY)[(si = vj)(pi= wj)];
б) tT така, що граф G = (X, F) переводить у граф H = (Y, P).

Доведення. Необхідність випливає із леми 3.1, а достатність – із леми 3.2.

F) і H = (Y, P), які мають n вершин

із попарно різними числами (s, p) і (v, w), то встановити їх ізоморфізм можна не більше, ніж за n(n+1)/2 порівнянь, причому підстановка tT така, що граф G = (X, Y) переводить у граф H = (Y, P) і визначається графом відповідності, який має n ребер.

= (Y, P)

графа. За їх рівності переходимо до п.2, за нерівності –

до п.6.
2. Виписуємо всі елементи обох графів у природній упорядкованості та визначаємо пари (s, p) і (v, w) для кожного елемента.
3. Для кожного елемента x графа G = (X, F) шукаємо такий елемент y графа H = (Y, P), для якого виконується умова а теореми 3.1. Знайдені елементи x та y з'єднуємо ребром – будуємо граф відповідності. Переходимо до п. 4, у протилежному випадку – до п. 6.
4. Виписуємо підстановку, що визначається графом відповідності, і перевіряємо виконання умови б теореми 3.1. При виконанні умови переходимо до п. 5, у протилежному випадку – до п. 6.
5. Графи ізоморфні. 6. Графи неізоморфні.

F) і H = (Y, P) (слайд 11). Визначити, чи

ізоморфні вони.
1. Встановлюємо, що кількість вершин графів G = (X, F) і H = (Y, P) однакова.
2. Записуємо вершини графів G = (X, F) та H = (Y, P) із парами (s, p) і (v, w), що їх характеризують.
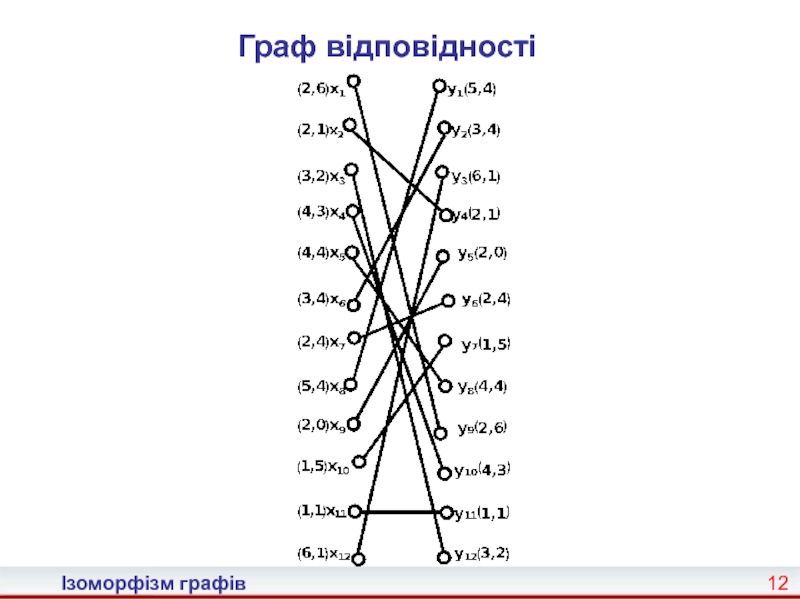
3. Будуємо граф відповідності (слайд 12).
4. Підстановка

t =

переводить матрицю суміжності графа G =(X, F) у матрицю суміжності графа H = (Y, P).
5. Графи G = (X, F) і H = (Y, P) ізоморфні.

Приклад застосування алгоритму

У випадку, коли графи G = (X, F) і H

= (Y, P) мають k (kn) вершин з однаковими парами (s, p) і (v, w) кожний, при використанні алгоритму одержимо k! підстановок замість однієї за попарно різних чисел (s, p) і (v, w). У даному разі слід перевірити виконання умови б теореми 3.1 для k! підстановок, що зменшує ефективність алгоритму.

(при переборі) можна запропонувати такий метод. Після запису всіх елементів

xX і yY обох графів з віднесеними для них парами чисел (s, p) і (v, w) з'єднуємо ребрами ті елементи графів, які задовольняють умову а теореми 3.1 і не входять до означених вище k вершин. Одержуємо часткову підстановку. Для елементів з однаковими парами (s, p) і (v, w) обох графів записуємо у дужках множини X'X та Y'Y, зіставлені елементам x та y, що розглядаються, відношеннями F і P відповідних графів. Для елементів xX' виписуємо елементи yY, які визначаються одержаною частковою підстановкою. З'єднуємо ребрами ті елементи xX та yY із вказаних k елементів, для яких множина Y' є однаковою.

елементів графів G = (X, F) і H =(Y, P)

присутні l елементів (lk), в яких множина Y' однакова для всіх l елементів і неможливо провести ребра графа відповідності, то для кожного елемента x та y обох графів записуємо у дужках множини X''X та Y''Y, зіставлені елементам x та y відношеннями F–1 і P–1, що є оберненими до відношень F і P. Для елементів xX'' виписуємо елементи yY, що визначаються частковою підстановкою, і поєднуємо ребрами графа відповідності ті елементи xX та yY з l елементів, що мають одну й ту саму множину Y''. Процес продовжуємо до одержання однієї або кількох підстановок замість k!, і після перевірки умови б теореми 3.1 робимо висновки про ізоморфізм графів.

(Y, P)
за наявності вершин
з однаковими парами
(s, p) і (v, w)

двох графів. Щоб не повторювати наведений вище алгоритм, запишемо в

ньому замість п.3 два нові пункти: 3 та 3 а.

= (Y, P) мають вершини із різними парами (s, p)

і (v, w) кожний, то будуємо граф відповідності шляхом поєднання ребрами таких елементів x та y графів G = (X, F) і H = (Y, P), для яких виконується умова а теореми 3.1. У противному випадку переходимо до п. 6. Якщо графи мають k (kn) вершин з однаковими парами (s, p) і (v, w) кожний, то спочатку поєднуємо ребрами елементи обох графів, що задовольняють умові а теореми 3.1 і не входять в означені k вершин. Одержуємо часткову підстановку.
3 а. Використовуємо запропонований метод для елементів з однаковими парами (s, p) і (v, w) й одержуємо одну або кілька підстановок замість k! Переходимо до п. 4.

Узагальнений алгоритм (2)

коли графи G=(X,F) і H = (Y, P) містять k1,

k2, ..., km елементів (k1 + k2 + ... + km

і H = (Y, P) (слайд 21). Чи ізоморфні вони?
Запишемо

елементи xX та yY обох графів із відповідними їм парами чисел (s, p) і (v, w) та визначимо часткову підстановку за рахунок проведення ребер 1 і 2 (слайд 22). Далі відповідно до викладеного методу послідовно проводимо ребра 3–7 з використанням відношень F, P і часткових підстановок.

Приклад визначення ізоморфізму графів

P) прикладу 3.4

G = (X, F) і H = (Y, P) ізоморфні.

t =

Сформована підстановка