2.5. Понятие кристаллического класса. Порядок записи элементов в симметрии

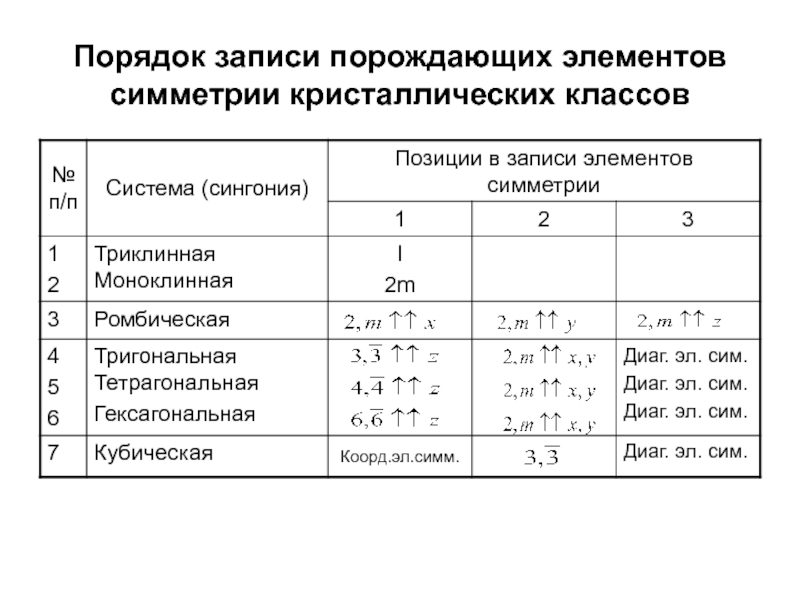
классов.
Для кристаллов (объектов, обладающих трансляционно повторяющейся структурой) свойственны следующие элементы

симметрии:

Возможные сочетания этих элементов симметрии друг с другом образуют различные кристаллические классы.


Определение: полная совокупность элементов симметрии, присущих кристаллу с данным типом структуры, называется кристаллическом классом.

симметрии кристаллических классов (Гадолинские группы симметрии).
Гадолин Аксель Вильгельмович (1828 -

1892) – генерал артиллерии, военный инженер. В 1867г. Вывел 32 точечные группы симметрии.

Совокупность 9 элементов симметрии структуры и трансляции (перенос на величину элементарной трансляции или периода повторяемости) образуют сочетания, которые называют пространственными группами симметрии (Федоровскими группами).
Федоров Евграф Степанович (1853-1919) – академик РАН. В 1890 г. – вывел 230 пространственных групп симметрии (Федоровских групп симметрии).

называется формулой симметрии.

на первой позиции указывают оси симметрии высших порядков;
на

второй позиции указывают наличие осей симметрии второго порядка (если они есть);
на третьей позиции указывают наличие плоскостей симметрии;
на четвертой позиции – центр инверсии (при его наличии).