2.8 Статистический смысл выборочных показателей

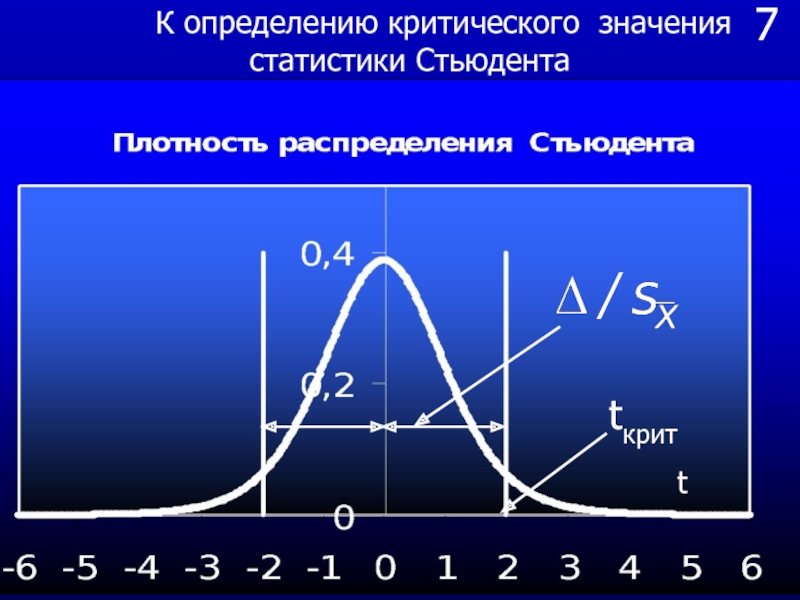
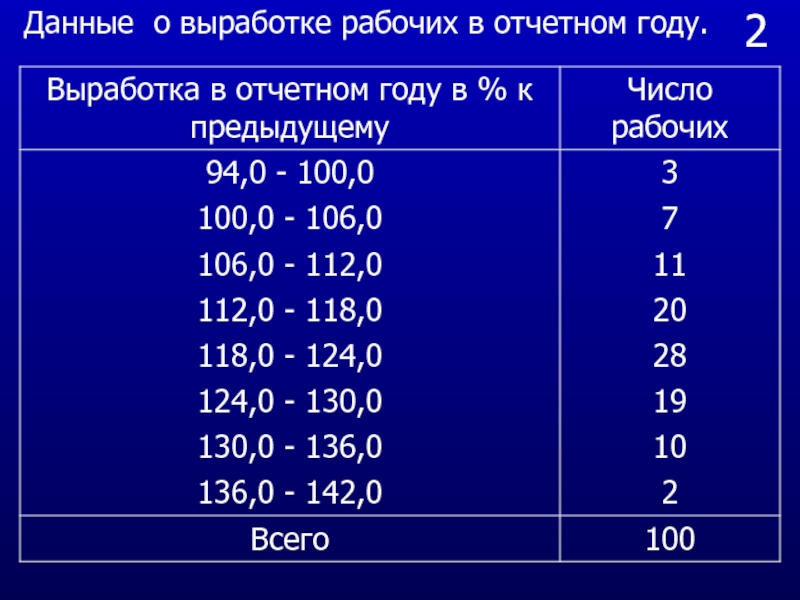
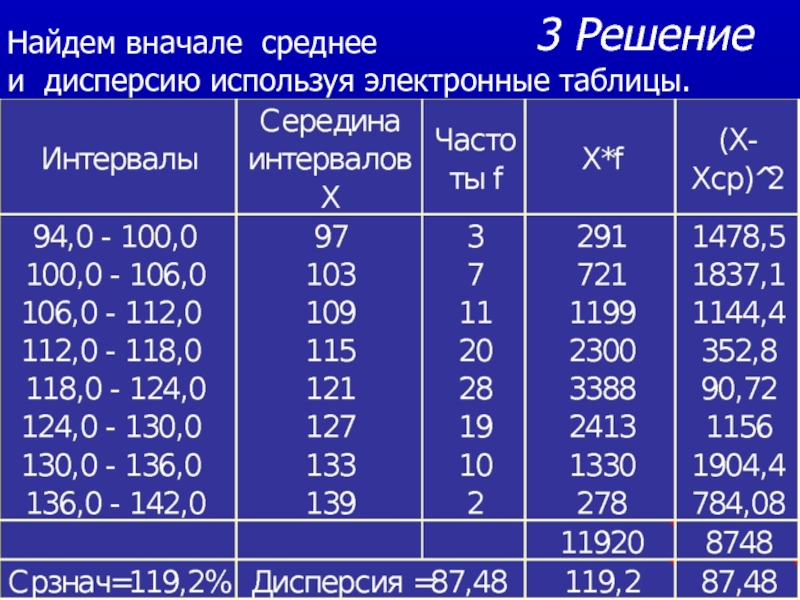
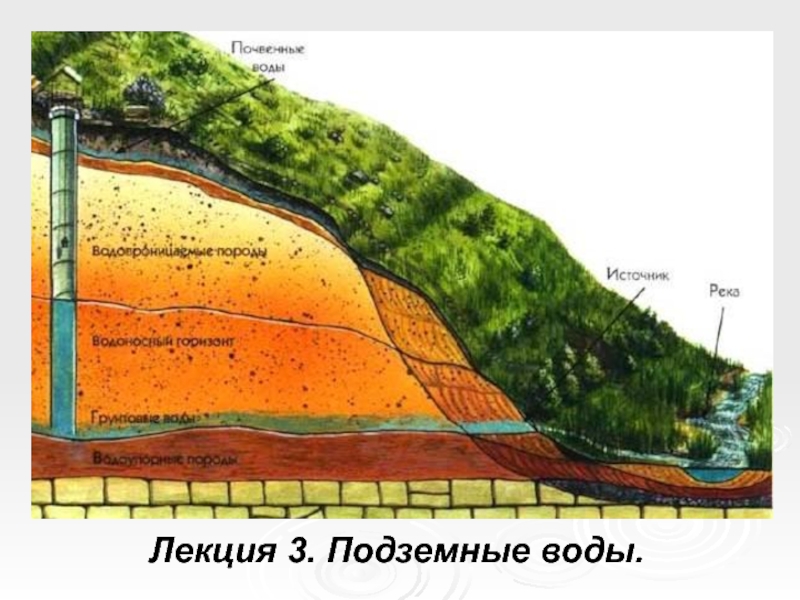
из генеральной совокупности, то для каждой выборки мы получим свои

значения показателей (средних значений, дисперсий и т. д.), которые, например, для среднего значения признака X образуют ряд:

Теперь, если число выборок устремить к бесконечности, то получится кривая частот, которая представляет собой кривую выборочного распределения.
Таким образом выборочные показатели являются случайными величинами.

в генеральной совокупности (конечность средних и ограниченность дисперсии), выборочное распределение

является нормальным, а его параметры совпадают с параметрами распределения изучаемого вариационного признака в генеральной совокупности.
Сделанные выше утверждения являются основой применения выборочного метода для изучения социально-экономических явлений.
Это замечание важно потому, что эконометрист всегда имеет дело с выборочной совокупностью.

x1, x2, x3 …xn .
Следует найти наилучшую оценку для

генеральной средней.
Оценкой случайной величины Х называется некоторая функция

В частности, если речь идет о среднем значении, то в качестве оценки можно выбрать выражение

полусумму максимального и минимального значений. Какая оценка является наилучшей?

Назвать наилучшей ту оценку, которая наиболее близка к истинному значению параметра невозможно, так как оценка является случайной величиной.
О качестве оценки следует судить не по ее индивидуальному значению, а по распределению ее значений в большом числе испытаний. Чем меньше рассеяние случайной величины относительно истинного значения, тем лучше оценка.

равно ее истинному значению при любом объеме выборки
В противном

случае оценка называется смещенной.
Оценка параметра Х называется состоятельной, если она удовлетворяет закону больших чисел

и при увеличении объема выборки оценка приближается к истинному значению (в качестве случайной величины здесь взято среднее значение).

Используемые оценки не всегда являются эффективными, поскольку для эффективной оценки

формулы могут оказаться слишком сложными.

Доказательство . Пусть выборочная средняя определяется формулой
Будем рассматривать

как случайные величины. Эти случайные величины имеют одинаковые параметры распределения (дисперсию и среднее значение).
Докажем, что математическое ожидание выборочной средней равно генеральной средней.

распределения, что и случайная величина Х в генеральной совокупности, то

математическое ожидание

Поскольку каждая из величин

Отсюда сразу получаем

Найдем дисперсию среднего арифметического одинаково распреде-ленных случайных величин
В

этой формуле буквой D обозначена дисперсия аргумента, дисперсия в генеральной совокупности.

Найдем дисперсию выборочной средней.

можно использовать для оценки по порядку величины отклонение выборочной

средней от генеральной средней.

При этом ошибка конкретной выборки может принимать различные значения, и она зависит от объема выборки и среднего квадратического отклонения в генеральной совокупности.

неизвестной величиной и ее нужно оценить по выборочной дисперсии.

Если в качестве оценки генеральной дисперсии взять значение выборочной дисперсии, то такая оценка получается смещенной и дает заниженное значение генеральной дисперсии, приводя к систематической ошибке.

используют исправленную
выборочную дисперсию , математическое ожидание

которой равно генеральной дисперсии:

При больших объемах выборки исправленная дисперсия несущественно отличается от выборочной. Доказательство этой формулы можно найти в учебниках по мат. статистике.

производили одним числом. Такая оценка называется точечной.
В ряде

задач нужно не только найти для параметра подходящую численную оценку, но и указать интервал значений параметра, который с заданной вероятностью «накроет» неизвестное значение параметра в генеральной совокупности.
Такая оценка параметра называется интервальной.

( ) , который

с заданной вероятностью накрывает неизвестное значение параметра Х. Важно отметить, что и
определяются по выборочному наблюдению.

отклонения, обозначив его буквой t:
Эта величина подчиняется распределению Стьюдента

с числом степеней свободы k=n-1, где n - объем выборки.

Построим доверительный интервал для генеральной средней в случае большой повторной выборки (n велико).

чтобы вероятность отклонения выборочной средней от генеральной средней :
была допустимой

для данного исследования.
Вероятность, которая принимается при расчете выборочной характеристики, называется доверительной вероятностью.

заданной доверительной вероятностью накроет среднее значение

мы должны потребовать выполнение равенства

где

вероятность того, что модуль отклонения

Или иначе

с помощью функции Excel СТЬЮДРАСПОБР(q;k), q =(1-P); где Р -

доверительная вероятность, находим критическое значение величины t.
Сказанное выше легко может быть проиллюстрировано на графике (см. след. слайд).

по сравнению с предыдущим по схеме собственно - случайной выборки

было отобрано 100 рабочих (полученные данные изображены на след. слайде).
Определить:
а) вероятность того, что средняя выработка рабочих цеха отличается от средней выборочной не более чем на 1%;
б) границы в которых с вероятностью 0,95 заключена средняя выработка рабочих цеха.

= 1 %), k=7
Таким образом, вероятность того,

что выборочная средняя отличается от генеральной не более чем на 1% равна 0, 7. Можно сказать, что в 70 случаях из 100 произведенное выборочное исследование даст ошибку определения средней производительности труда для всего цеха не более чем 1%.

будет находиться средняя выработка рабочих цеха. Опять используем условие
Из

таблиц для распределения Стьюдента, находим значение аргумента t. Это значение равно 2,3. Поэтому

Таким образом, генеральная средняя будет с вероятностью 0,95 находиться в интервале