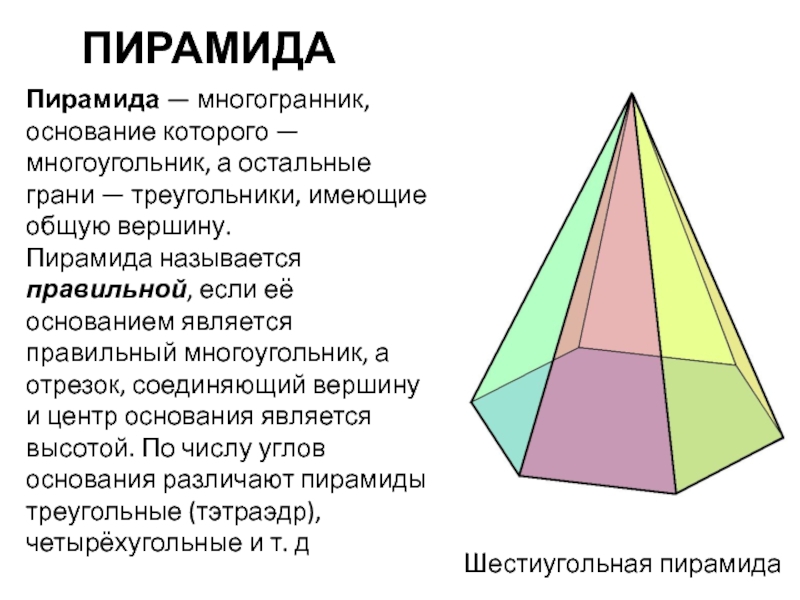
общую вершину.
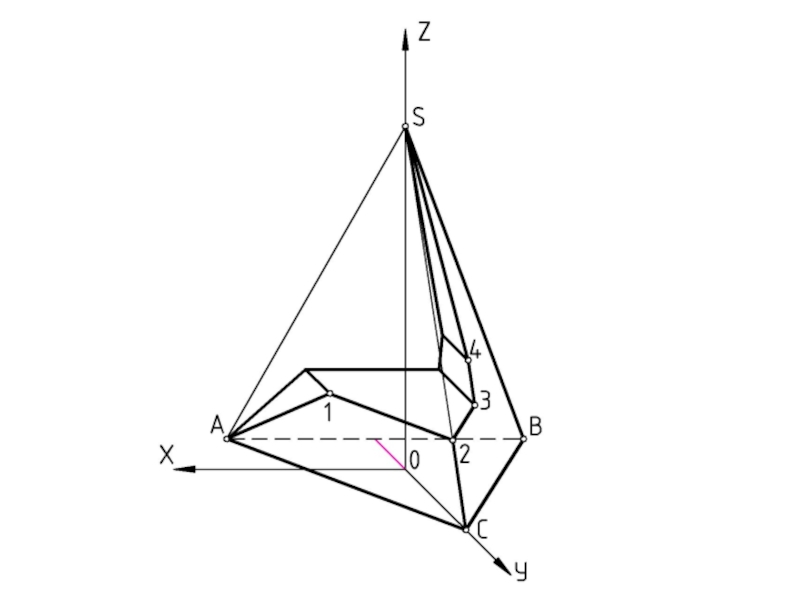
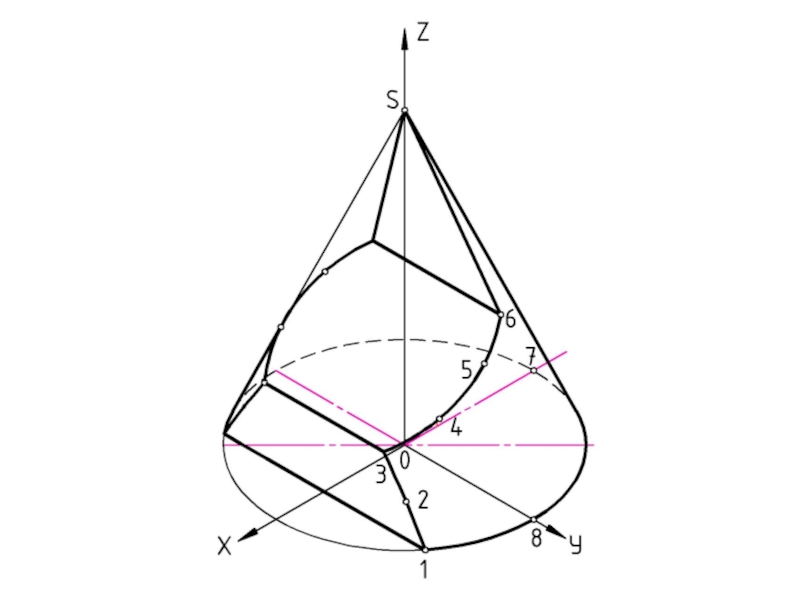
Пирамида называется правильной, если её основанием является правильный многоугольник,
а отрезок, соединяющий вершину и центр основания является высотой. По числу углов основания различают пирамиды треугольные (тэтраэдр), четырёхугольные и т. дШестиугольная пирамида
ПИРАМИДА