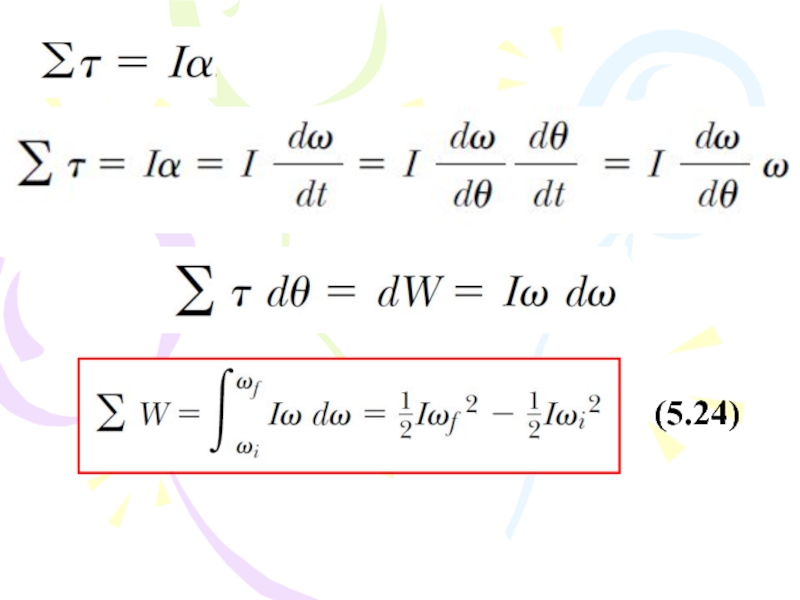Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Contemporary physics
Содержание
- 1. Contemporary physics
- 2. Figure 4.1. Two particles interact with each
- 3. The linear momentum of a particle or
- 4. As you can see from its definition,
- 5. Using Newton’s second law of motion, we
- 6. Using the definition of momentum, Equation 4.1
- 7. This result, known as the law of
- 8. The momentum of a particle changes if
- 9. (4.9)To evaluate the integral, we need to
- 10. The direction of the impulse vector is
- 11. Because the force imparting an impulse can
- 12. We use the term collision to represent
- 13. The total momentum of an isolated system
- 14. An inelastic collision is one in which
- 15. Figure 4.4 Schematic representation of a perfectly
- 16. Figure 4.5 Schematic representation of an elastic
- 17. Next, let us separate the terms containing
- 18. Suppose that the masses and initial velocities
- 19. If particle 2 is initially at rest,
- 20. The momentum of a system of two
- 21. Figure 4.6 An elastic glancing collision between two particles.glancing collision(4.25)(4.24)
- 22. (4.26)If the collision is elastic, we can
- 23. Figure 4.7 Two particles of unequal mass
- 24. Figure 4.8 The center of mass of
- 25. (4.30)Figure 4.9 An extended object can be
- 26. Assuming M remains constant for a system
- 27. If we now differentiate Equation 4.34 with
- 28. That is, the net external force on
- 29. The angular position of the rigid object
- 30. Rotation of a Rigid Object About a
- 31. The average angular accelerationThe instantaneous angular accelerationWhen
- 32. Direction for angular speed and angular accelerationFigure
- 33. Rotational Kinematics: Rotational Motion with Constant Angular
- 34. (5.7)is the angular position of the rigid
- 35. If we eliminate t from Equations 5.6
- 36. Table 5.1
- 37. Angular and Linear QuantitiesFigure 5.4 As a
- 38. We can relate the angular acceleration of
- 39. Figure 5.5 As a rigid object rotates
- 40. Rotational Kinetic EnergyFigure 10.7 A rigid object rotating about the z axis with angular speed ω.(5.14)
- 41. We simplify this expression by defining the
- 42. Calculation of Moments of Inertia(5.17)
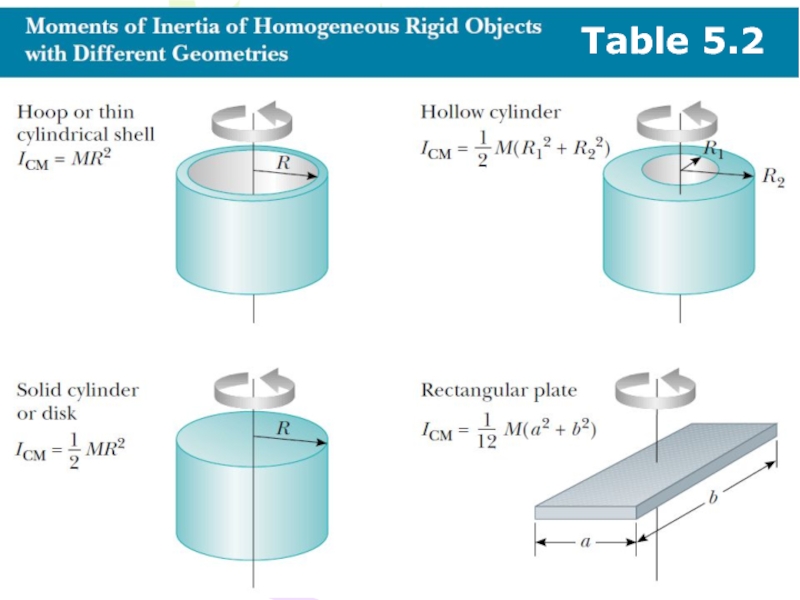
- 43. Table 5.2
- 44. Слайд 44
- 45. TorqueFigure 5.8 The force F has a
- 46. Figure 5.9 The force F1 tends to
- 47. Relationship Between Torque and Angular AccelerationFigure 5.10
- 48. The torque acting on the particle is
- 49. Figure 5.11 A rigid object rotating about an axis through O.
- 50. Although each mass element of the rigid
- 51. Work, Power, and Energy in Rotational MotionFigure
- 52. The rate at which work is being
- 53. (5.24)
- 54. That is, the work–kinetic energy theorem for
- 55. Table 5.3
- 56. Rolling Motion of a Rigid ObjectFigure 5.13
- 57. Figure 5.14 All points on a rolling
- 58. Figure 5.15 The motion of a rolling
- 59. Find v1f and v2f. QuizFigure 4.5 Schematic
- 60. Quick Quiz 1 A block of mass
- 61. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Course of lectures «Contemporary Physics: Part1»
Lecture №5
Linear Momentum and Collisions.
Rotation
of a Rigid Object about a Fixed Axis.
Слайд 2Figure 4.1. Two particles interact with each other. According to
Newton’s third law, we must have F12 = - F21.
Слайд 3The linear momentum of a particle or an object that
can be modeled as a particle of mass m moving
with a velocity v is defined to be the product of the mass and velocity:(4.1)
(4.2)
Linear momentum is a vector quantity because it equals the product of a scalar quantity m and a vector quantity v. Its direction is along v, it has dimensions ML/T, and its SI unit is kg · m/s.
Слайд 4As you can see from its definition, the concept of
momentum provides a quantitative distinction between heavy and light particles
moving at the same velocity. For example, the momentum of a bowling ball moving at 10 m/s is much greater than that of a tennis ball moving at the same speed. Newton called the product mv quantity of motion; this is perhaps a more graphic description than our present-day word momentum, which comes from the Latin word for movement.If a particle is moving in an arbitrary direction, p must have three components
Слайд 5Using Newton’s second law of motion, we can relate the
linear momentum of a particle to the resultant force acting
on the particle. We start with Newton’s second law and substitute the definition of acceleration:(4.3)
As m=const:
The time rate of change of the linear momentum of a particle is equal to the net force acting on the particle.
Слайд 6Using the definition of momentum, Equation 4.1 can be written
where
p1i and p2i are the initial values and p1f and
p2f the final values of the momenta for the two particles for the time interval during which the particles interact.(4.5)
(4.4)
Слайд 7This result, known as the law of conservation of linear
momentum, can be extended to any number of particles in
an isolated system. It is considered one of the most important laws of mechanics. We can state it as follows:Whenever two or more particles in an isolated system interact, the total momentum of the system remains constant.
This law tells us that the total momentum of an isolated system at all times equals its initial momentum.
Notice that we have made no statement concerning the nature of the forces acting on the particles of the system. The only requirement is that the forces must be internal to the system.
(4.6)
Слайд 8The momentum of a particle changes if a net force
acts on the particle.
According to Newton’s second law
(4.7)
(4.8)
Слайд 9(4.9)
To evaluate the integral, we need to know how the
force varies with time. The quantity on the right side
of this equation is called the impulse of the force F acting on a particle over the time interval ∆t=tf - ti. Impulse is a vector defined byEquation 4.8 is an important statement known as the impulse–momentum theorem:
The impulse of the force F acting on a particle equals the change in the momentum of the particle.
Слайд 10The direction of the impulse vector is the same as
the direction of the change in momentum. Impulse has the
dimensions of momentum—that is, ML/T. Note that impulse is not a property of a particle; rather, it is a measure of the degree to which an external force changes the momentum of the particle. Therefore, when we say that an impulse is given to a particle, we mean that momentum is transferred from an external agent to that particle.Figure 4.2 (a) A force acting on a particle may vary in time. The impulse imparted to the particle by the force is the area under the force-versus-time curve. (b) In the time interval (t, the time-averaged force (horizontal dashed line) gives the same impulse to a particle as does the time-varying force described in part (a).
(a)
(b)
Слайд 11Because the force imparting an impulse can generally vary in
time, it is convenient to define a time-averaged force
where ∆t=tf
- ti. (4.10)
(4.12)
The calculation becomes especially simple if the force acting on the particle is constant. In this case, and Equation 4.11 becomes
In many physical situations, we shall use what is called the impulse approximation, in which we assume that one of the forces exerted on a particle acts for a short time but is much greater than any other force present.
(4.11)
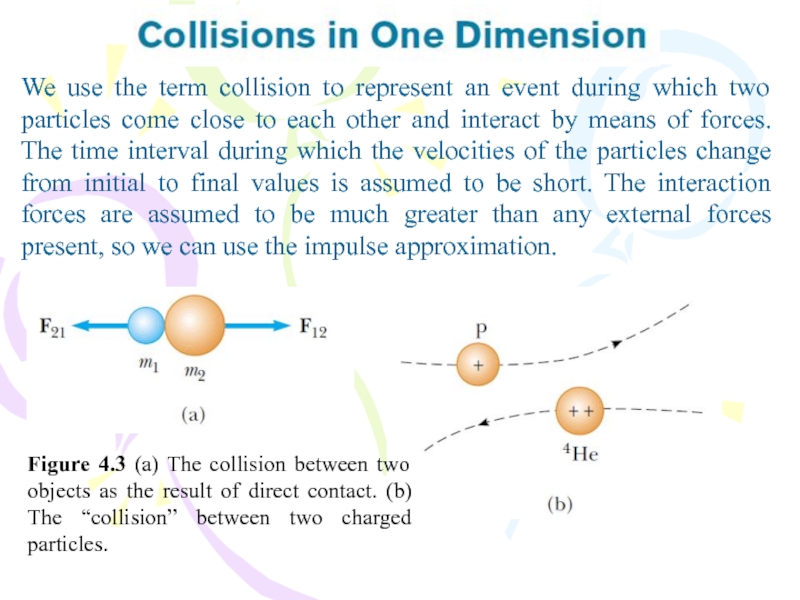
Слайд 12We use the term collision to represent an event during
which two particles come close to each other and interact
by means of forces. The time interval during which the velocities of the particles change from initial to final values is assumed to be short. The interaction forces are assumed to be much greater than any external forces present, so we can use the impulse approximation.Figure 4.3 (a) The collision between two objects as the result of direct contact. (b) The “collision” between two charged particles.
Слайд 13 The total momentum of an isolated system just before a
collision equals the total momentum of the system just after
the collision.The total kinetic energy of the system of particles may or may not be conserved, depending on the type of collision. In fact, whether or not kinetic energy is conserved is used to classify collisions as either elastic or inelastic.
An elastic collision between two objects is one in which the total kinetic energy (as well as total momentum) of the system is the same before and after the collision. Collisions between certain objects in the macroscopic world, such as billiard balls, are only approximately elastic because some deformation and loss of kinetic energy take place. For example, you can hear a billiard ball collision, so you know that some of the energy is being transferred away from the system by sound. An elastic collision must be perfectly silent! Truly elastic collisions occur between atomic and subatomic particles.
Слайд 14An inelastic collision is one in which the total kinetic
energy of the system is not the same before and
after the collision (even though the momentum of the system is conserved).Inelastic collisions are of two types.
When the colliding objects stick together after the collision, as happens when a meteorite collides with the Earth, the collision is called perfectly inelastic.
When the colliding objects do not stick together, but some kinetic energy is lost, as in the case of a rubber ball colliding with a hard surface, the collision is called inelastic (with no modifying adverb).
In most collisions, the kinetic energy of the system is not conserved because some of the energy is converted to internal energy and some of it is transferred away by means of sound. Elastic and perfectly inelastic collisions are limiting cases; most collisions fall somewhere between them.
The important distinction between these two types of collisions is that momentum of the system is conserved in all collisions, but kinetic energy of the system is conserved only in elastic collisions.
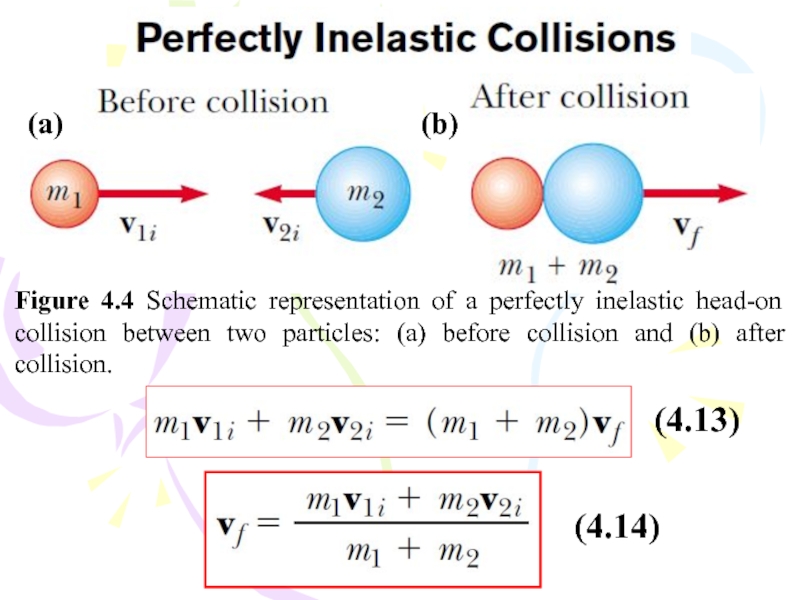
Слайд 15Figure 4.4 Schematic representation of a perfectly inelastic head-on collision
between two particles: (a) before collision and (b) after collision.
(a)
(b)
(4.13)
(4.14)
Слайд 16Figure 4.5 Schematic representation of an elastic head-on collision between
two particles: (a) before collision and (b) after collision.
(4.15)
(4.16)
Слайд 17Next, let us separate the terms containing m1 and m2
in Equation 4.15 to obtain
(4.17)
(4.18)
(4.19)
To obtain our final result, we
divide Equation 4.17 by Equation 4.18 and obtainСлайд 18Suppose that the masses and initial velocities of both particles
are known.
(4.20)
(4.21)
Let us consider some special cases. If m1 =
m2, then Equations 4.20 and 4.21 show us that v1f = v2i and v2f = v1i .That is, the particles exchange velocities if they have equal masses. This is approximately what one observes in head-on billiard ball collisions - the cue ball stops, and the struck ball moves away from the collision with the same velocity that the cue ball had.
Слайд 19If particle 2 is initially at rest, then v2i =
0, and Equations 4.20 and 4.21 become
(4.22)
(4.23)
If m1 is much
greater than m2 and v2i = 0, we see from Equations 4.22 and 4.23 that v1f ≈ v1i and v2f ≈ 2v1i .If m2 is much greater than m1 and particle 2 is initially at rest, then v1f ≈ -v1i and v2f ≈ 0.
Слайд 20The momentum of a system of two particles is conserved
when the system is isolated. For any collision of two
particles, this result implies that the momentum in each of the directions x, y, and z is conserved.For such two-dimensional collisions, we obtain two component equations for conservation of momentum:
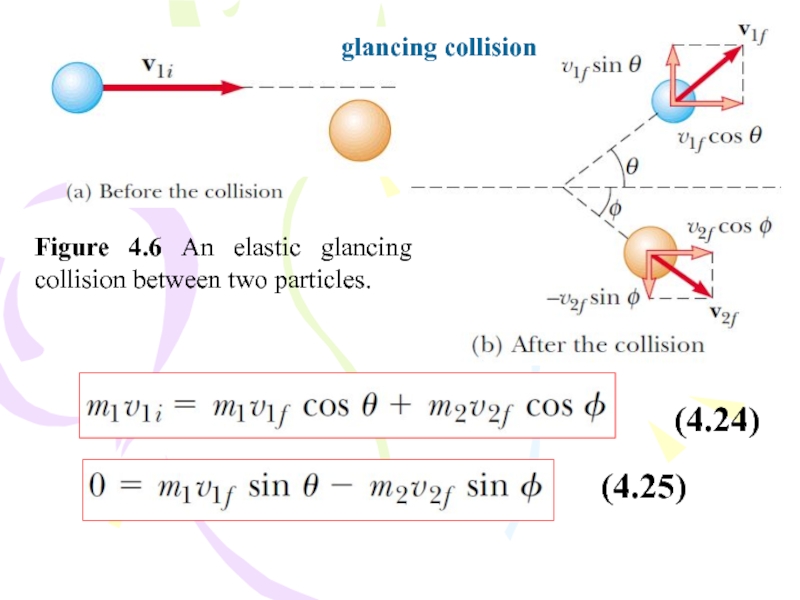
Слайд 21Figure 4.6 An elastic glancing collision between two particles.
glancing collision
(4.25)
(4.24)
Слайд 22(4.26)
If the collision is elastic, we can also use Equation
4.16 (conservation of kinetic energy) with v2i = 0 to
giveIf the collision is inelastic, kinetic energy is not conserved and Equation 4.26 does not apply.
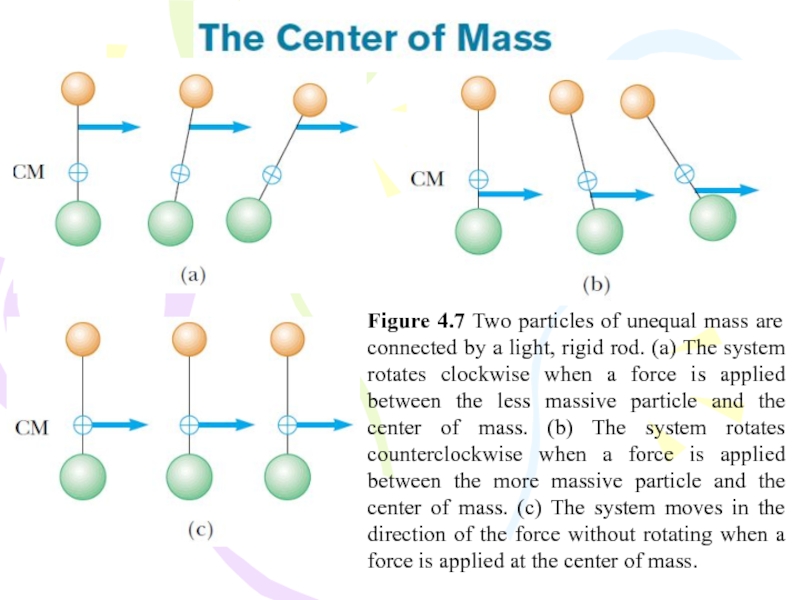
Слайд 23Figure 4.7 Two particles of unequal mass are connected by
a light, rigid rod. (a) The system rotates clockwise when
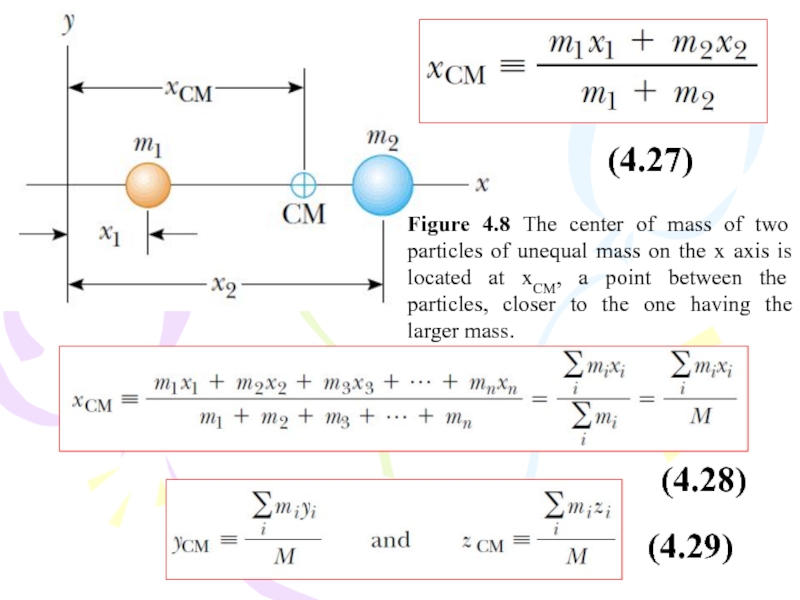
a force is applied between the less massive particle and the center of mass. (b) The system rotates counterclockwise when a force is applied between the more massive particle and the center of mass. (c) The system moves in the direction of the force without rotating when a force is applied at the center of mass.Слайд 24Figure 4.8 The center of mass of two particles of
unequal mass on the x axis is located at xCM,
a point between the particles, closer to the one having the larger mass.(4.27)
(4.28)
(4.29)
Слайд 25(4.30)
Figure 4.9 An extended object can be considered to be
a distribution of small elements of mass ∆mi. The center
of mass is located at the vector position rCM, which has coordinates xCM, yCM, and zCM.The center of mass of any symmetric object lies on an axis of symmetry and on any plane of symmetry.
a continuous mass distribution
Слайд 26Assuming M remains constant for a system of particles, that
is, no articles enter or leave the system, we obtain
the following expression for the velocity of the center of mass of the system:where vi is the velocity of the ith particle. Rearranging Equation 4.34 gives
(4.34)
(4.35)
Therefore, we conclude that the total linear momentum of the system equals the total mass multiplied by the velocity of the center of mass. In other words, the total linear momentum of the system is equal to that of a single particle of mass M moving with a velocity vCM.
Слайд 27If we now differentiate Equation 4.34 with respect to time,
we obtain the acceleration of the center of mass of
the system:Rearranging this expression and using Newton’s second law, we obtain
where Fi is the net force on particle i.
(4.36)
(4.37)
Слайд 28That is, the net external force on a system of
particles equals the total mass of the system multiplied by
the acceleration of the center of mass. If we compare this with Newton’s second law for a single particle, we see that the particle model that we have used for several chapters can be described in terms of the center of mass:The center of mass of a system of particles of combined mass M moves like an equivalent particle of mass M would move under the influence of the net external force on the system.
(4.38)
Слайд 29The angular position of the rigid object is the angle
θ between this reference line on the object and the
fixed reference line in space, which is often chosen as the x axis.Figure 5.1 A compact disc rotating about a fixed axis through O perpendicular to the plane of the figure.
Rotation of a Rigid Object About a Fixed Axis
(5.1)
Слайд 30Rotation of a Rigid Object About a Fixed Axis
Figure 5.2
A particle on a rotating rigid object moves from A
to B along the arc of a circle. In the time interval ∆t = tf - ti , the radius vector moves through an angular displacement ∆θ = θf - θi.The average angular speed
The instantaneous angular speed
(5.2)
(5.3)
Слайд 31The average angular acceleration
The instantaneous angular acceleration
When a rigid object
is rotating about a fixed axis, every particle on the
object rotates through the same angle in a given time interval and has the same angular speed and the same angular acceleration.(5.4)
(5.5)
Слайд 32Direction for angular speed and angular acceleration
Figure 5.3 The right-hand
rule for determining the direction of the angular velocity vector.
Слайд 33Rotational Kinematics: Rotational Motion with Constant Angular Acceleration
(5.6)
is the angular
speed of the rigid object at time t = 0.
Equation
5.6 allows us to find the angular speed ωf of the object at any later time t.Слайд 34(5.7)
is the angular position of the rigid object at time
t = 0.
Equation 5.7 allows us to find the angular
position θf of the object at any later time t.Слайд 35If we eliminate t from Equations 5.6 and 5.7, we
obtain
This equation allows us to find the angular speed ωf
of the rigid object for any value of its angular position θf .If we eliminate α between Equations 5.6 and 5.7, we obtain
(5.8)
(5.9)
Слайд 37Angular and Linear Quantities
Figure 5.4 As a rigid object rotates
about the fixed axis through O, the point P has
a tangential velocity v that is always tangent to the circular path of radius r.(5.10)
That is, the tangential speed of a point on a rotating rigid object equals the perpendicular distance of that point from the axis of rotation multiplied by the angular speed.
Слайд 38We can relate the angular acceleration of the rotating rigid
object to the tangential acceleration of the point P by
taking the time derivative of v:That is, the tangential component of the linear acceleration of a point on a rotating rigid object equals the point’s distance from the axis of rotation multiplied by the angular acceleration.
(5.11)
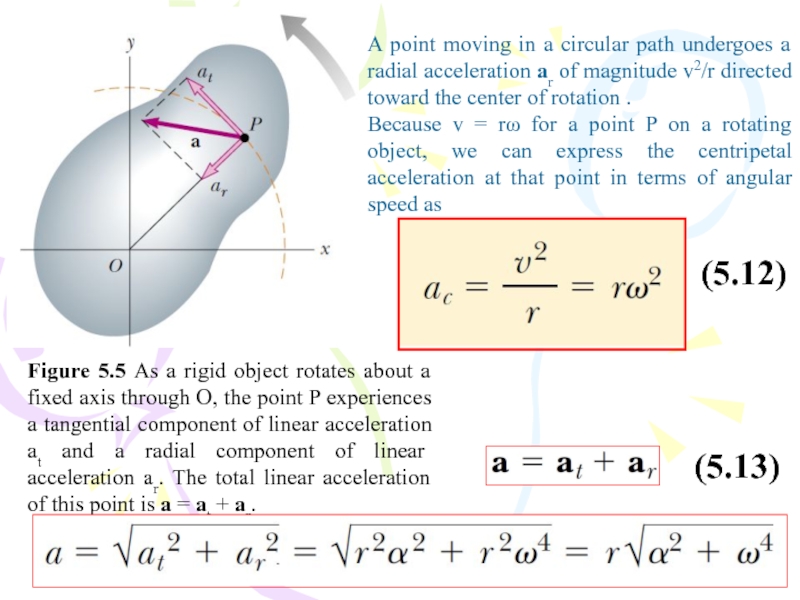
Слайд 39Figure 5.5 As a rigid object rotates about a fixed
axis through O, the point P experiences a tangential component
of linear acceleration at and a radial component of linear acceleration ar. The total linear acceleration of this point is a = at + ar.A point moving in a circular path undergoes a radial acceleration ar of magnitude v2/r directed toward the center of rotation .
Because v = rω for a point P on a rotating object, we can express the centripetal acceleration at that point in terms of angular speed as
(5.12)
(5.13)
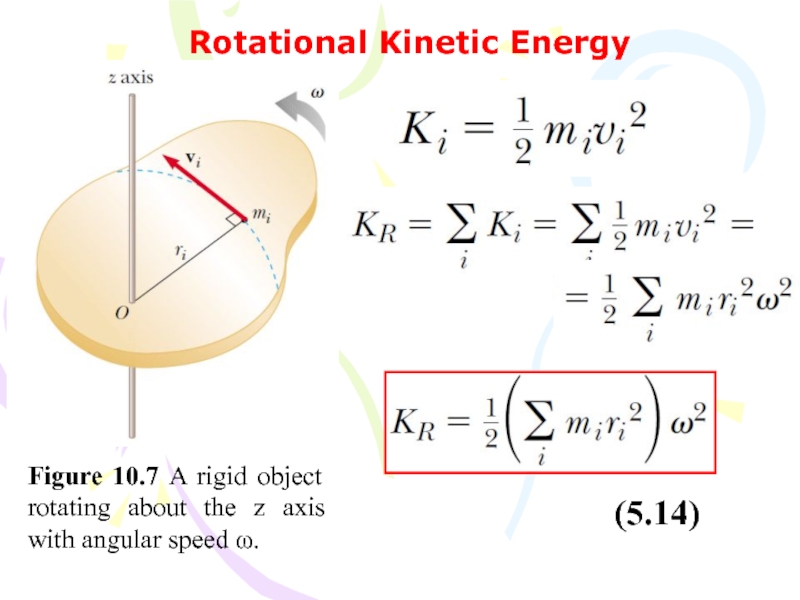
Слайд 40Rotational Kinetic Energy
Figure 10.7 A rigid object rotating about the
z axis with angular speed ω.
(5.14)
Слайд 41We simplify this expression by defining the quantity in parentheses
as the moment of inertia I:
From the definition of moment
of inertia, we see that it has dimensions of ML2 (kg ·m2 in SI units). With this notation, Equation 5.14 becomes(5.15)
Where KR is Rotational kinetic energy.
(5.16)
Слайд 45Torque
Figure 5.8 The force F has a greater rotating tendency
about O as F increases and as the moment arm
d increases. The component Fsinφ tends to rotate the wrench about O.When a force is exerted on a rigid object pivoted about an axis, the object tends to rotate about that axis. The tendency of a force to rotate an object about some axis is measured by a vector quantity called torque τ (Greek tau).
(5.18)
Слайд 46Figure 5.9 The force F1 tends to rotate the object
counterclockwise about O, and F2 tends to rotate it clockwise.
(5.19)
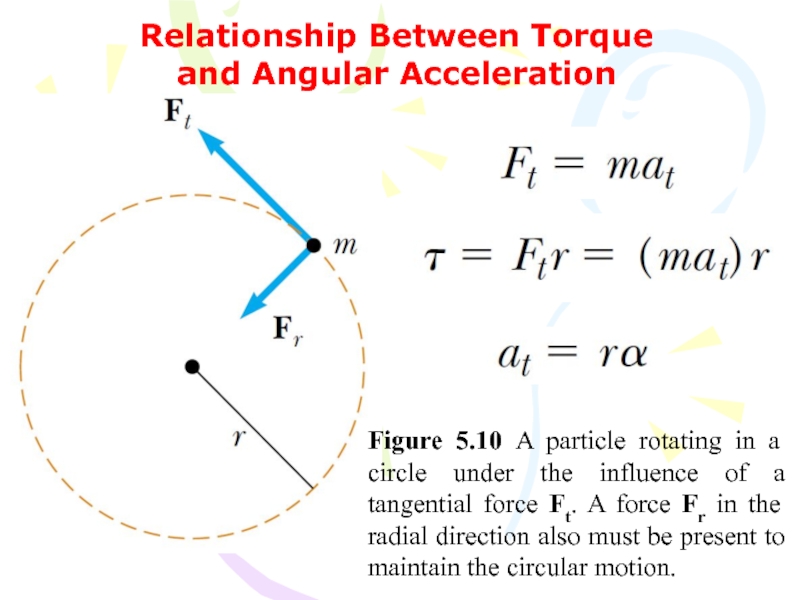
Слайд 47Relationship Between Torque and Angular Acceleration
Figure 5.10 A particle rotating
in a circle under the influence of a tangential force
Ft. A force Fr in the radial direction also must be present to maintain the circular motion.Слайд 48The torque acting on the particle is proportional to its
angular acceleration, and the proportionality constant is the moment of
inertia.(5.20)
Слайд 50Although each mass element of the rigid object may have
a different linear acceleration at , they all have the
same angular acceleration α.So, again we see that the net torque about the rotation axis is proportional to the angular acceleration of the object, with the proportionality factor being I, a quantity that depends upon the axis of rotation and upon the size and shape of the object.
(5.21)
Слайд 51Work, Power, and Energy in Rotational Motion
Figure 5.12 A rigid
object rotates about an axis through O under the action
of an external force F applied at P.The work done by F on the object as it rotates through an infinitesimal distance
where Fsinφ is the tangential component of F, or, in other words, the component of the force along the displacement.
(5.22)
Слайд 52The rate at which work is being done by F
as the object rotates about the fixed axis through the
angle dθ in a time interval dt is(5.23)
Слайд 54That is, the work–kinetic energy theorem for rotational motion states
that
the net work done by external forces in rotating a
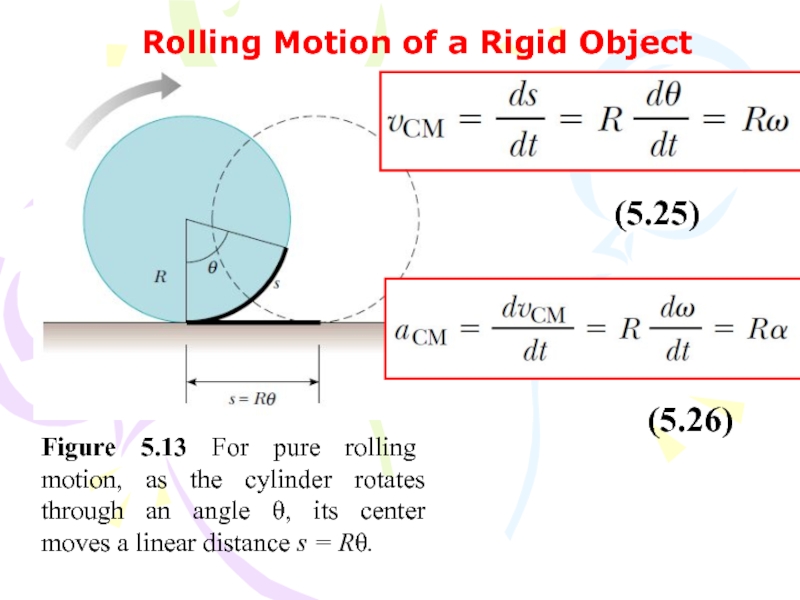
symmetric rigid object about a fixed axis equals the change in the object’s rotational energy.Слайд 56Rolling Motion of a Rigid Object
Figure 5.13 For pure rolling
motion, as the cylinder rotates through an angle θ, its
center moves a linear distance s = Rθ.(5.25)
(5.26)
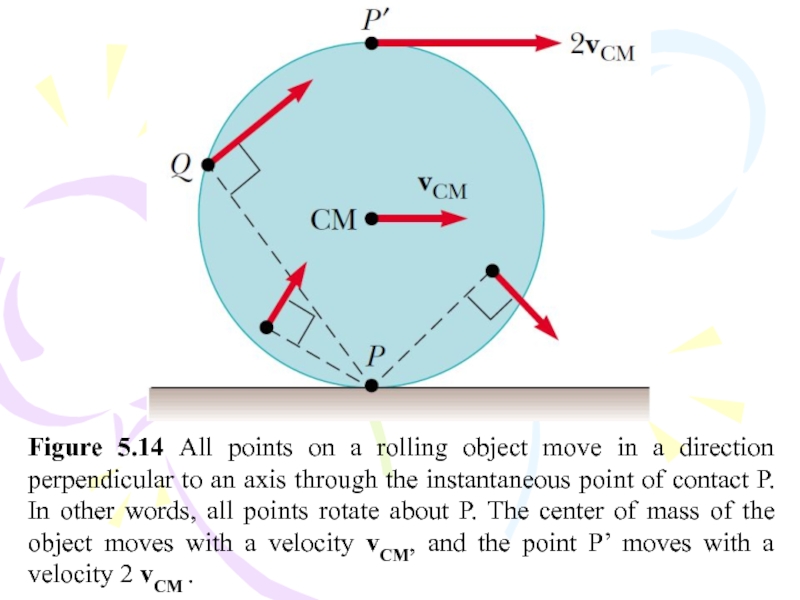
Слайд 57Figure 5.14 All points on a rolling object move in
a direction perpendicular to an axis through the instantaneous point
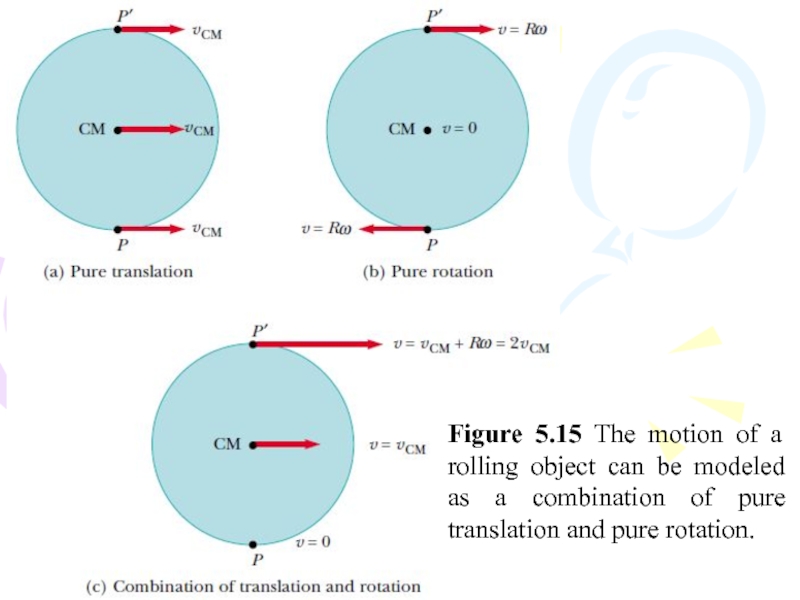
of contact P. In other words, all points rotate about P. The center of mass of the object moves with a velocity vCM, and the point P’ moves with a velocity 2 vCM .Слайд 58Figure 5.15 The motion of a rolling object can be
modeled as a combination of pure translation and pure rotation.
Слайд 59Find v1f and v2f.
Quiz
Figure 4.5 Schematic representation of an
elastic head-on collision between two particles: (a) before collision and
(b) after collision.Слайд 60Quick Quiz 1 A block of mass m is projected
across a horizontal surface with an initial speed v. It
slides until it stops due to the friction force between the block and the surface. The same block is now projected across the horizontal surface with an initial speed 2v. When the block has come to rest, how does the distance from the projection point compare to that in the first case? (a) It is the same. (b) It is twice as large. (c) It is four times as large. (d) The relationship cannot be determined.Quick Quiz 2 A car and a large truck traveling at the same speed make a head-on collision and stick together. Which vehicle experiences the larger change in the magnitude of momentum? (a) the car (b) the truck (c) The change in the magnitude of momentum is the same for both. (d) impossible to determine.