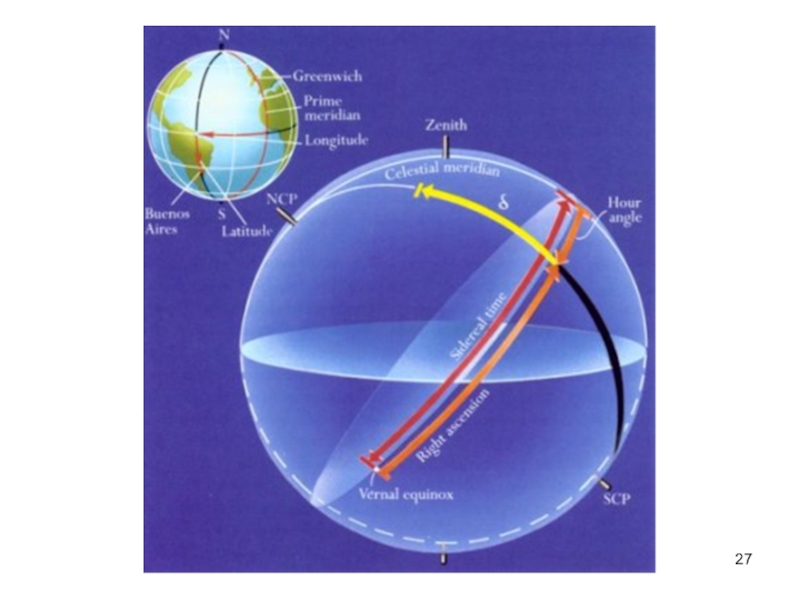
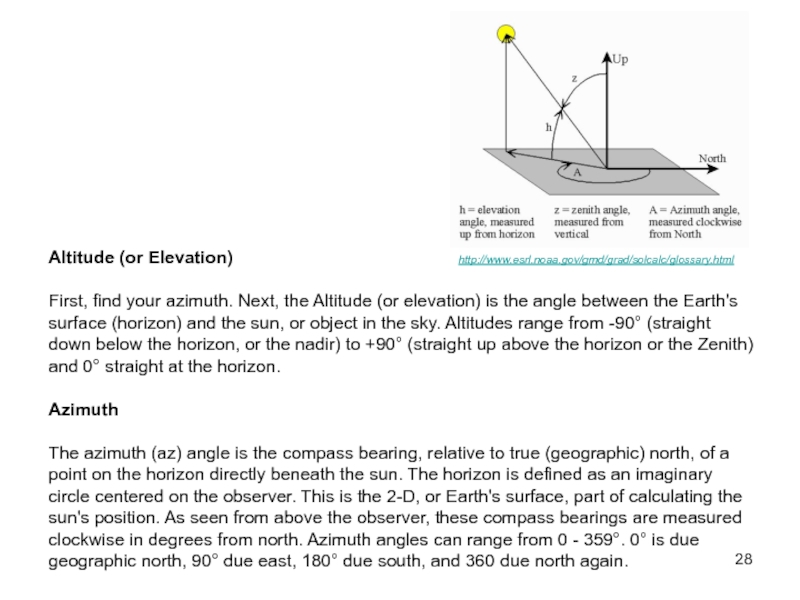
(or elevation) is the angle between the Earth's surface (horizon)
and the sun, or object in the sky. Altitudes range from -90° (straight down below the horizon, or the nadir) to +90° (straight up above the horizon or the Zenith) and 0° straight at the horizon.
Azimuth
The azimuth (az) angle is the compass bearing, relative to true (geographic) north, of a point on the horizon directly beneath the sun. The horizon is defined as an imaginary circle centered on the observer. This is the 2-D, or Earth's surface, part of calculating the sun's position. As seen from above the observer, these compass bearings are measured clockwise in degrees from north. Azimuth angles can range from 0 - 359°. 0° is due geographic north, 90° due east, 180° due south, and 360 due north again.
http://www.esrl.noaa.gov/gmd/grad/solcalc/glossary.html