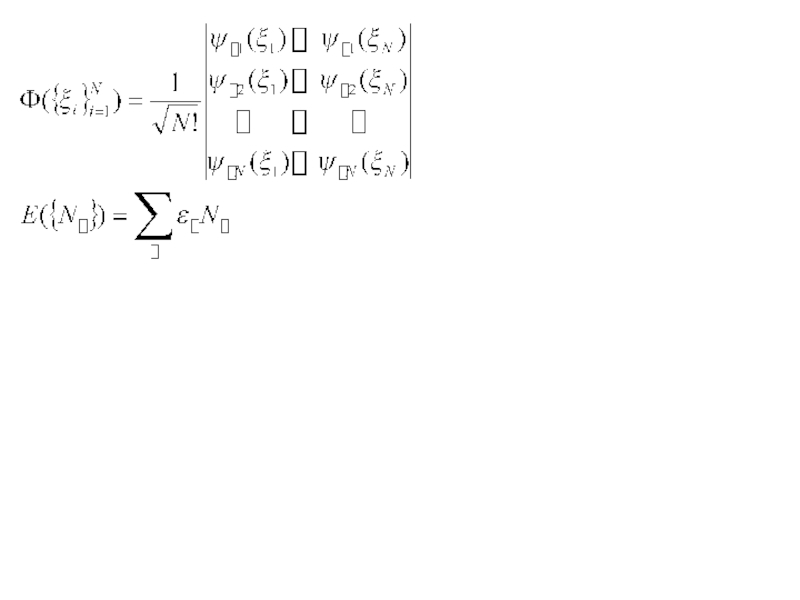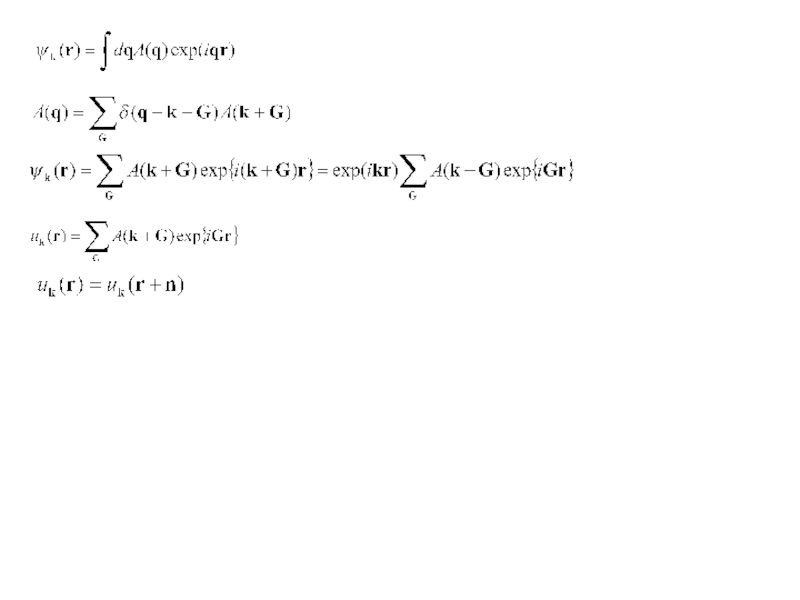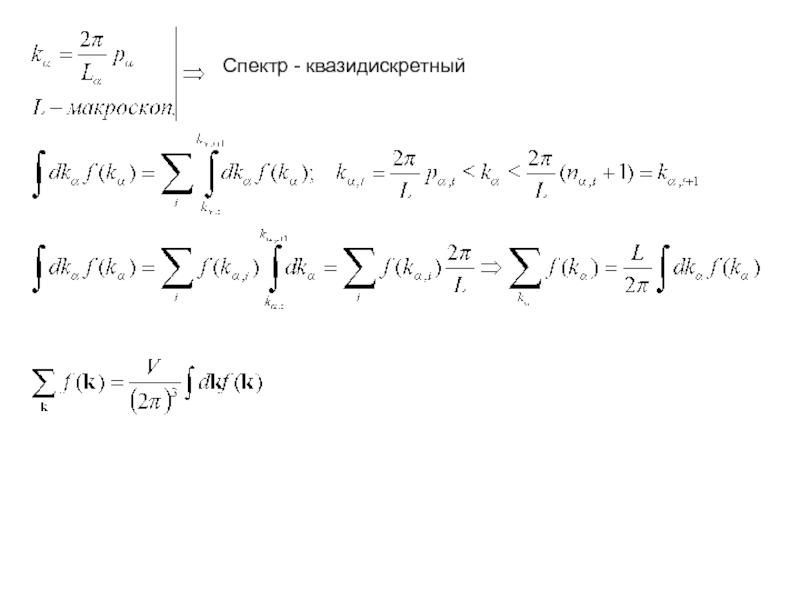Адиабатическое приближение в твердом теле

электрон-электронного взаимодействия
- энергия взаимодействия электронов с ядрами
- энергия ион-ион взаимодействия
Основная

проблема – макроскопически большое число взаимодействующих частиц => нужно решать УШ с макроскопическим числом неразделяющихся переменных => нужны приближения

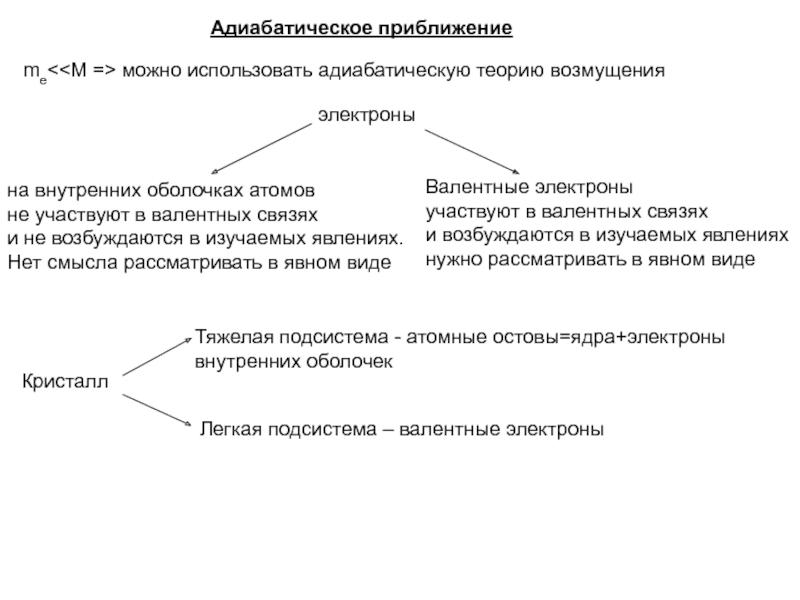
атомов
не участвуют в валентных связях
и не возбуждаются в изучаемых явлениях.

Нет смысла рассматривать в явном виде

Валентные электроны
участвуют в валентных связях
и возбуждаются в изучаемых явлениях
нужно рассматривать в явном виде

Кристалл

Тяжелая подсистема - атомные остовы=ядра+электроны внутренних оболочек

Легкая подсистема – валентные электроны

под мгновенное положение ионов)=>энергетический спектр и волновые функции стационарных состояний

электронов можно определять, считая ионы неподвижными

- Базис при фиксированных R

R - параметры

ищем базис из стационарных состояний кристалла в виде

умножаем обе части на φ* и интегрируем по r

СУШ для ионов во внешнем поле εe(R) =>
=> Можно сформировать

базис из α(R) => из произведений ψ=αφ можно сформировать базис для кристалла

Задача о состояниях кристалла

Задача о состояниях электронов
В поле неподвижных ядер

Задача о стационарных состояниях ядер
В эффективном среднем поле εe(R), создаваемом электронами

ядер
Проблема та же – из-за взаимодействия между частицами нужно решать

УШ с огромным числом неразделяющихся переменных

что каждый электрон, “чувствует” некоторое среднее поле Ueff(r), создаваемое всеми

остальными электронами, т.е. в замене многоэлектронного взаимодействия некоторым эффективным полем.

Электрон-электронное взаимодействие учитываем путем введения эффективного поля Ueff(r), внешнего по отношению к системе электронов.

Система взаимодействующих электронов заменяется на систему невзаимодейсивующих электронов, находящихся во внешнем поле Ueff(r)

же силовых полях, что и весь газ)
Находим одноэлектронные стационарные состояния

– состояния одного отдельно взятого электрона, рассмотренного в тех же силовых полях, что и весь газ

- Одноэлектронный спектр и базис из в.ф. одноэлектронных стационарных состояний

2) В стационарном состоянии всей системы в целом каждый из электронов находится в одном из одночастичных стационарных состояний. Поэтому стационарное состояние всего газа в целом однозначным образом задается указанием чисел заполнения всех одночастичных стационарных состояний

Электроны – фермионы => подчиняются принципу запрета Паули =>
числа заполнения могут принимать только два значения

создаваемое средней электронной плотностью
Поле Хартри – самосогласованное поле: определяет одноэлектронные

волновые функции и при этом само зависит от этих функций. Должно определяться так, чтобы оно давало волновые функции, приводящие к тому же полю.

- Поле Хартри

механики


Наилучшее приближение для волновой функции получается, когда
δε=0 => одноэлектронное уравнение

Шредингера

Не учитываем перестановочную симметрию => самосогласованное поле Хартри




Учитываем перестановочную симметрию=> самосогласованное поле Хартри-Фока

обменное взаимодействие

в положении равновесия (хорошая нулевая задача)

Идеальный кристалл => поле ионов

– периодическое с периодом решетки

Электронейтральность => средняя электронная плотность имеет период решетки => самосогласованное поле – периодическое с периодом решетки

Кристаллическое поле – периодическое с периодом решетки

Е является вырожденным?
Е вырожден с кратностью s =>
лин. незав.
Решения

УШ с энергией Е

Любая линейная комбинация решений – тоже решение с той же энергией

Нужно подобрать такие коэффициенты в этих линейных комбинациях, чтобы система

из s решений (*) была линейно независимой и при этом каждая из функций (*) удовлетворяла условию

- ОСЛАУ

точках, отстоящих друг от друга на вектор решетки.
В различных

стационарных состояниях эта связь будет разной => Значения вектора k в различных состояниях будут отличаться. Поэтому вектор k следует рассматривать как квантовое число, характеризующее заданное стационарное состояния.

удовлетворяет условию
Обратная решетка

поле

Cтационарное состояние электрона в периодическом поле кристаллической решетки задается

двумя квантовыми числами – волновым вектором Блоха k и натуральным индексом (номер зоны).

себя все физически различные значения вектора Блох и не содержащая

физически эквивалентные его значения

- непрерывна в пределах зоны Бриллюэна

- -ая энергетическая зона

условия призваны отражать физическую картину на границе кристалла, как правило

очень сложную.

Решение: Силы быстро убывают с расстоянием => в глубине кристалла граница не ощущается => в объемных кристаллах можно срезать приграничную область, и рассматривать только внутренний объем, в котором влиянием границы можно пренебречь.

Внутренний объем разбиваем на одинаковые макроскопические параллелепипеды, построенные на векторах элементарных трансляций.

Кристалл – периодическая структура => Все параллелепипеды – физически эквивалентны => разумно потребовать, чтобы

Физическая эквивалентность параллелепипеда (в среднем все одинаково) => достаточно рассмотреть только один параллелепипед с граничными условиями

Бриллюэна.

Сколько физически различных значений волнового вектора Блоха?

Выбор зоны Бриллюэна

– вопрос удобства. Возьмем в качестве зоны Бриллюэна параллелепипед, построенный на векторах элементарных трансляций обратной решетки

экстремума зоны
Идеальный кристалл
Блоховский базис
- нулевая задача
- возмущение
Рассчитываем блоховские состояния в

точке экстремума k=0.
Закон дисперсии в окрестности точки экстремума определяем с помощью теории возмущения

инверсии
сдвиг точки экстремума

виде