Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра Кабанов Александр Николаевич к.ф.-м.н., доцент кафедры кибернетики
Содержание
- 1. Алгебра Кабанов Александр Николаевич к.ф.-м.н., доцент кафедры кибернетики
- 2. 3. Линейные пространства
- 3. Линейное пространствоМножество элементов V называется линейным или
- 4. Линейное пространствоНа множестве V определена замкнутая операция
- 5. Линейное пространствоДистрибутивность умножения на число относительно сложения
- 6. Линейное пространствоСуществование нейтрального элемента по сложению, т.е.
- 7. Пример линейного пространстваТривиальным примером линейного пространства будет
- 8. Линейная комбинацияПусть a1, …, an – элементы
- 9. Линейная зависимостьЭлементы называются линейно зависимыми, если существует
- 10. Свойства линейной зависимостиЕсли среди элементов есть такой,
- 11. БазисНабор элементов линейного пространства называется базисом этого
- 12. Разложение по базисуТеорема (о разложении вектора по
- 13. Разложение по базисуТаким образом, если a1, …,
- 14. Уточнение определенияТаким образом, следует уточнить определение базиса.Базисом
- 15. Проверка базисаПусть у нас есть n-мерное линейное
- 16. Проверка базисаЕсли элементов в наборе ровно n,
- 17. Дополнение до базисаТеорема (о дополнении до базиса):
- 18. Переход к новому базисуПусть B1 = {e1,
- 19. Матрица переходаЭту систему можно записать в матричном
- 20. Матрица переходаТаким образом, матрица перехода состоит из
- 21. Координаты вектора в новом базисеПусть вектор x
- 22. ПодпространствоЕсли подмножество линейного пространства удовлетворяет всем свойствам
- 23. Сумма подпространствСуммой подпространств U и V линейного
- 24. Пересечение подпространствПересечение подпространств U и V линейного
- 25. Линейная оболочкаЛинейной оболочкой векторов называется совокупность всех
- 26. Евклидово пространствоЛинейное пространство называется евклидовым, если любым
- 27. Скалярное произведениеСкалярное произведение может задаваться любым образом
- 28. НормаДлиной или нормой вектора x в евклидовом
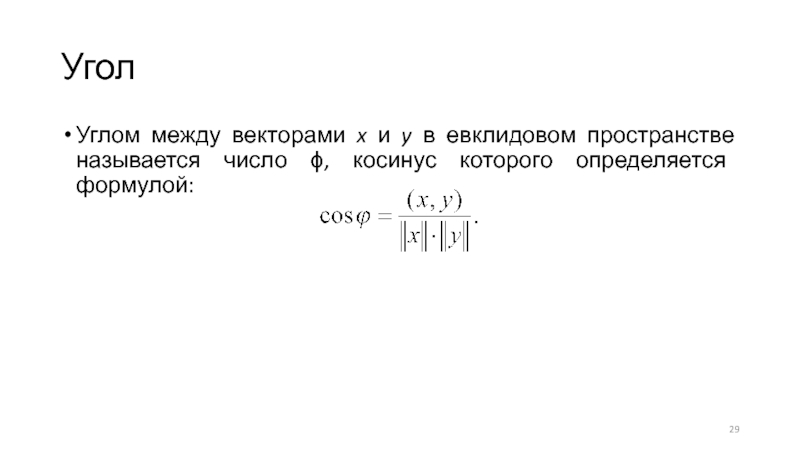
- 29. УголУглом между векторами x и y в евклидовом пространстве называется число ϕ, косинус которого определяется формулой:
- 30. Свойства нормыДля любого вектора x и любого
- 31. Ортогональные вектораДва ненулевых вектора называются ортогональными, если
- 32. Ортонормированная системаСистема векторов называется ортогональной, если все
- 33. Ортонормированная системаЗамечание: Чтобы нормировать вектор, нужно разделить
- 34. ОртобазисТеорема (о независимости ортонормированной системы): Любая ортонормированная
- 35. Метод Грама-ШмидтаПусть мы имеем базис пространства f1,
- 36. Метод Грама-ШмидтаВ качестве вектора g2 возьмем вектор
- 37. Метод Грама-ШмидтаДалее, в качестве вектора g3 возьмем
- 38. Скачать презентанцию
3. Линейные пространства
Слайды и текст этой презентации
Слайд 3Линейное пространство
Множество элементов V называется линейным или векторным пространством над
действительными числами, если выполняются следующие условия.
операция суммы элементов, т.е. любым двум элементам x, y из пространства V ставится в соответствие некоторый элемент z из пространства V, который называется их суммой и обозначается z = x + y.Слайд 4Линейное пространство
На множестве V определена замкнутая операция умножения элемента на
число, т.е. любому элементу x из пространства V и любому
действительному числу λ ставится в соответствие некоторый элемент z из пространства V, который называется произведением числа λ на элемент x и обозначается z = λ·x = λx.На множестве должны быть справедливы следующие аксиомы.
Коммутативность сложения: x + y = y + x.
Ассоциативность сложения: (x + y) + z = x + (y + z).
Слайд 5Линейное пространство
Дистрибутивность умножения на число относительно сложения элементов: λ(x +
y) = λx + λy.
Дистрибутивность умножения на число относительно сложения
чисел: (λ + μ)x = λx + μx.Ассоциативность умножения на число: (λμ)x = λ(μx).
Существование нейтрального элемента по умножению на число: 1·x = x.
Слайд 6Линейное пространство
Существование нейтрального элемента по сложению, т.е. в пространстве V
существует такой элемент 0, что x + 0 = x
для любого элемента x из пространства V.Существование противоположного элемента по сложению, т.е. для любого элемента x из пространства V существует такой элемент (–x) в пространстве V, что x + (–x) = 0.
Слайд 7Пример линейного пространства
Тривиальным примером линейного пространства будет так называемое пустое
пространство – пространство состоящее из одного 0.
Другим примером является пространство
n-мерных векторов, т.е. векторов, состоящих из n компонент или координат.Слайд 8Линейная комбинация
Пусть a1, …, an – элементы линейного пространства V.
Элемент
x = λ1a1 + … + λnan, где коэффициенты λ1,
..., λn – произвольные действительные числа, называется линейной комбинацией элементов a1, …, an.Линейная комбинация, в которой все коэффициенты одновременно равны нулю, называется тривиальной.
Слайд 9Линейная зависимость
Элементы называются линейно зависимыми, если существует их нетривиальная линейная
комбинация, равная нулю.
Если линейная комбинация элементов может быть равна 0,
только если все коэффициенты равны 0, то такие элементы называются линейно независимыми.Слайд 10Свойства линейной зависимости
Если среди элементов есть такой, который является линейной
комбинацией части остальных, то весь набор элементов является линейно зависимым.
Если
среди элементов есть нулевой, то элементы линейно зависимы.Если элемент является линейной комбинацией линейно независимых элементов, то коэффициенты в его разложении определяются единственным образом.
Слайд 11Базис
Набор элементов линейного пространства называется базисом этого пространства, если эти
элементы линейно независимы, а добавление любого другого элемента делает набор
линейно зависимым.В общем случае базис в пространстве можно выбрать разными способами. Базисов может быть даже бесконечное множество.
Но количество элементов в любом базисе одного и того же пространства V всегда одинаково. Это число называется размерностью линейного пространства и обозначается dim V.
Слайд 12Разложение по базису
Теорема (о разложении вектора по базису): Каждый элемент
линейного пространства можно представить в виде линейной комбинации элементов выбранного
базиса, и притом единственным образом.Эта линейная комбинация называется разложением элемента (или вектора) по базису. А коэффициенты в линейной комбинации называются координатами этого элемента (или вектора).
Слайд 13Разложение по базису
Таким образом, если a1, …, an – базис
линейного пространства V, то элемент x можно единственным образом представить
в виде x = λ1a1 + … + λnan.Для упрощения записи элемент x можно записывать как совокупность его координат в этом базисе x = (λ1, …, λn).
Для того, чтобы при работе с базисом не запутаться в координатном представлении элементов, набор базисных элементов необходимо упорядочить, т.е. пронумеровать.
Очевидно, что по-разному упорядоченный базис будет давать разные координатные представления одного и того же элемента.
Слайд 14Уточнение определения
Таким образом, следует уточнить определение базиса.
Базисом называется упорядоченный линейно
независимый набор элементов линейного пространства, через линейную комбинацию которых можно
представить любой элемент пространства.Слайд 15Проверка базиса
Пусть у нас есть n-мерное линейное пространство V.
Чтобы ответить
на вопрос, является ли данный набор элементов базисом, для начала
нужно обратить внимание на их количество.Если их меньше, чем n, то для базиса этого точно недостаточно. Если больше, то набор точно линейно зависим. В обоих случаях базисом набор не будет.
Слайд 16Проверка базиса
Если элементов в наборе ровно n, то нужно составить
из координатных представлений элементов матрицу и найти ее ранг.
Если ранг
меньше, чем n, то набор линейно зависим и, следовательно, базисом не является.Если же ранг равен n, то элементы линейно независимы, и поскольку их n, то они по определению будут составлять базис.
Слайд 17Дополнение до базиса
Теорема (о дополнении до базиса): Пусть в n-мерном
линейном пространстве V выбран набор k линейно независимых элементов (k
< n). Тогда в пространстве V существуют n – k элементов, добавление которых к этому набору даст базис линейного пространства V.Слайд 18Переход к новому базису
Пусть B1 = {e1, …, en} и
B2 = {f1, …, fn} – старый и новый базисы
линейного n-мерного пространства.Каждый вектор нового базиса можно выразить через старый базис: fi = ai1e1 + … + ainen, 1 ≤ i ≤ n.
Получаем систему уравнений:
f1 = a11e1 + … + a1nen,
...
fn = an1e1 + … + annen.
Слайд 19Матрица перехода
Эту систему можно записать в матричном виде:
Матрица, стоящая справа,
называется матрицей перехода от старого базиса к новому и обозначается
T.Слайд 20Матрица перехода
Таким образом, матрица перехода состоит из координат разложения векторов
нового базиса по старому базису, записанных по столбцам.
Свойства матрицы перехода:
Матрица
перехода является невырожденной.Если T – матрица перехода от старого базиса к новому, то матрица перехода от нового базиса к старому будет равна T-1.
Слайд 21Координаты вектора в новом базисе
Пусть вектор x имеет координаты (x1,
…, xn) = xe в старом базисе.
Координаты этого же вектора
в новом базисе можно выразить через матрицу перехода T от старого базиса к новому:xf = T-1xe.
Другими словами, xf = Tfexe.
Слайд 22Подпространство
Если подмножество линейного пространства удовлетворяет всем свойствам пространства, то оно
называется подпространством.
Любое линейное пространство обладает как минимум двумя подпространствами: нулевым
подпространством и подпространством, совпадающим с самим пространством.Эти 2 подпространства называются тривиальными.
Слайд 23Сумма подпространств
Суммой подпространств U и V линейного пространства L называется
подпространство
U+V = {x = u + v | u
U, v V}Если для любого элемента x из суммы подпространств разложение x = u + v единственно, то такая сумма называется прямой и обозначается UV.
Сумма подпространств может быть прямой, только если подпространства U и V не пересекаются между собой.
Слайд 24Пересечение подпространств
Пересечение подпространств U и V линейного пространства L так
же будет подпространством.
Размерности подпространств связаны следующим отношением:
dim (U+V) = dim
U + dim V – dim (UV)Слайд 25Линейная оболочка
Линейной оболочкой векторов называется совокупность всех линейных комбинаций этих
векторов.
Если X – некоторое множество векторов, то его линейная оболочка
обозначается L(X).Свойства линейной оболочки:
X L(X).
Если X – множество из линейного пространства V, то L(X) V и L(X) – подпространство пространства V.
Слайд 26Евклидово пространство
Линейное пространство называется евклидовым, если любым двум векторам x
и y из пространства ставится в соответствие некоторое число, обозначаемое
(x, y) и называемое их скалярным произведением.Слайд 27Скалярное произведение
Скалярное произведение может задаваться любым образом – главное, чтобы
выполнялись следующие условия для любых векторов x, y, z и
любого действительного числа λ:(x, y) = (y, x).
(x + y, z) = (x, z) + (y, z).
(λ∙x, y) = λ∙(x, y).
(x, x) > 0, если x ≠ 0.
(x, x) = 0, если x = 0.
Слайд 28Норма
Длиной или нормой вектора x в евклидовом пространстве называется число
В
2-х- и 3-хмерном векторном пространстве это понятие имеет ясный геометрический
смысл.Слайд 29Угол
Углом между векторами x и y в евклидовом пространстве называется
число ϕ, косинус которого определяется формулой:
Слайд 30Свойства нормы
Для любого вектора x и любого действительного числа λ
выполняются следующие условия:
‖x‖ = 0 тогда и только тогда, когда
x = 0. ‖λ∙x‖ = |λ|∙‖x‖
|(x, y)| ≤ ‖x‖∙‖y‖ (неравенство Коши-Буняковского)
‖x + y‖ ≤ ‖x‖ + ‖y‖ (неравенство треугольника)
Слайд 31Ортогональные вектора
Два ненулевых вектора называются ортогональными, если их скалярное произведение
равно 0.
Для 2-х- и 3-хмерного векторного пространства ортогональность векторов означает
их перпендикулярность.Неравенство треугольника для ортогональных векторов превращается в равенство: ‖x + y‖2 = ‖x‖2 + ‖y‖2.
Слайд 32Ортонормированная система
Система векторов называется ортогональной, если все вектора системы попарно
ортогональны.
Система векторов называется нормированной, если норма каждого вектора системы равна
1.Если система векторов одновременно ортогональная и нормированная, то такая система называется ортонормированной.
Слайд 33Ортонормированная система
Замечание: Чтобы нормировать вектор, нужно разделить его на его
норму.
Таким образом, если x – вектор евклидова пространства, то его
нормированная версия e = x / ‖x‖.Слайд 34Ортобазис
Теорема (о независимости ортонормированной системы): Любая ортонормированная система векторов линейна
независима.
Теорема (о существовании ортобазиса): В любом n-мерном евклидовом пространстве существует
ортонормированный базис.Таким образом, любую линейно независимую систему векторов можно преобразовать в ортонормированную.
Алгоритм, позволяющий это сделать, называется методом ортогонализации Грама-Шмидта.
Слайд 35Метод Грама-Шмидта
Пусть мы имеем базис пространства f1, f2, …, fn.
Будем
создавать новый ортогональный базис g1, g2, …, gn.
Нормируя его, получим
ортонормированный базис e1, e2, …, en.Возьмем в качестве вектора g1 вектор f1 и нормируем его, разделив на длину. Таким образом,
g1 = f1, e1 = g1/‖g1‖.
Слайд 36Метод Грама-Шмидта
В качестве вектора g2 возьмем вектор f2 – (f2,
e1)∙e1.
Несложно проверить, что если этот вектор умножить скалярно на e1,
то в результате получится 0, т.е. вектор g2 и e1 ортогональны.Таким образом,
g2 = f2 – (f2, e1)∙e1, e2 = g2/‖g2‖.
Слайд 37Метод Грама-Шмидта
Далее, в качестве вектора g3 возьмем вектор, ортогональный одновременно
и e1, и e2.
g3 = f3 – (f3, e1)∙e1 –
(f3, e2)∙e2, e3 = g3/‖g3‖.И так далее.
Общая формула выглядит следующим образом: