АСУ и САУ

автоматического управления

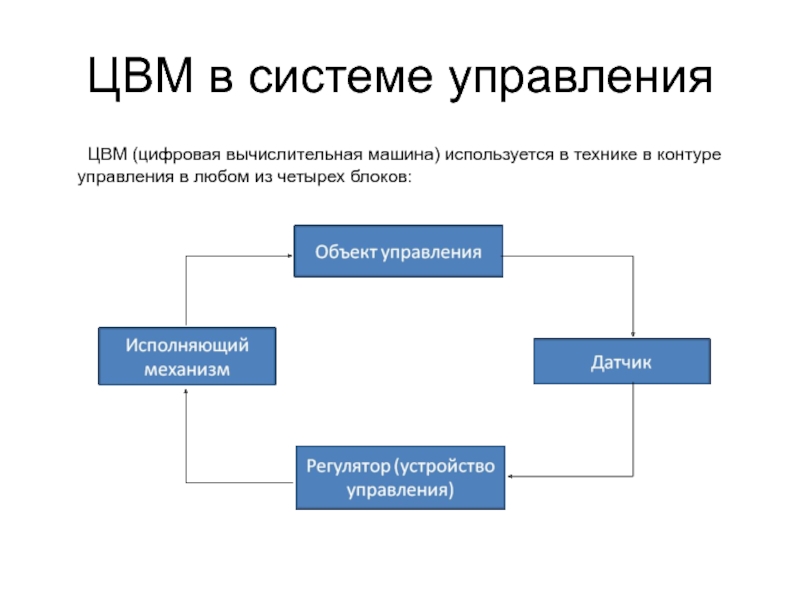
Основное отличие АСУ от САУ – в АСУ человек

участвует в процессе формирования управленческих воздействий (выполняет функции регулятора), им выполняются функции датчика, или выполняется функция использования механизма. В САУ человек не участвует в формировании управленческого воздействия.

Предназначение АСУ и САУ – облегчить, упростить, ускорить, сделать более точным и эффективным процесс управления.

Человек не всегда может переложить свои усилия на технические агрегаты по причинам:
1. Невозможность переложения.
2. Отсутствие желания
3. По причине сложности рационального распределения функций между человеком и агрегатами (исходя из моральных, экономических, политических, мировоззренческих, физиологических и психофизиологических оценок).

Функции человека в АСУ: анализ производственных обстоятельств, организация
процесса принятия и исполнения решений.

технике в контуре управления в любом из четырех блоков:

времени, определяемое сигналами задающего генератора
Соответствие языкового выражения целевой функции и

структуры вычислительного устройства (операнды – коммуникации, операторы – технические узлы)
Конечная арифметика и хранимая программа

m выходов.
На каждый вход устройства может быть подан произвольный символ

x из конечного входного алфавита X={x1,x2,…xk}.
Цифровое устройство будет работать нормально, если на вход будут приходить слова, а не отдельные символы входного алфавита.
Совокупность символов, поданных на вход устройство, образует входное слово Pi .
На выходе появляются выходные слова, состоящие из выходного алфавита Y={y1,y2,…yl}
Общее число входных и выходных слов конечно в силу конечности алфавитов X и Y.
В реальности x1,x2,…,xk – электрические, пневматические, гидравлические, световые, электронные сигналы. Их можно получить с помощью трения, нагревания, света и пьезоэффекта.

…

…

1

2

n

1

2

m

том, что при появлении на входе устройства входного слова Pi

устройство выдает на выходах комбинации выходных символов, образующих выходное слово Qj.

Такт работы – время, когда устройство выполняет свою функцию по формированию устройства.

входным словом. Тогда работа устройства будет определена, если мы зададим

следующую таблицу соответствия для всех входных слов:
P1 Qj1
P2 Qj2 (1)
…
Pkn Qjkn

В таблице kn строк по числу различных входных слов длины n над алфавитом X.

Устройство, условия работы которого описываются при помощи таблицы (1), называется конечным автоматом без памяти, или комбинационной схемой.

внутренних состояний. Предположим, что работа устройства полностью определена входным словом

и внутренним состоянием, в котором находится устройство в такт работы. Работа устройства полностью определена, если заданы две таблицы А и В следующего вида:
P1→Qi
{Pi(t), St(t)} → Qj(t)} (A)
{Pi(t), St(t)} → Sj(t+1)} (B)
Устройство, работа которого определяется таблицами А и В, называется конечным автоматом с глубиной памяти Q.
Конечные автоматы без памяти и с памятью являются устройствами детерминированного типа. Описание их работы в виде таблиц А и В есть задание жесткого алгоритма их работы. (см. следующий слайд)

готов к работе, когда задано начальное состояние. Начальное состояние определяет

kn выходных слов, и только конкретное входное слово определяет конкретное выходное слово.

f1(x1,x2)0
f2(x1,x2) – конъюнкция. f2(x1,x2)=x1&x2
f3(x1,x2) – x1 замещает x2. f3(x1,x2)=x1

x2
f4(x1,x2) – повтор x1. f4(x1,x2)  x1
f5(x1,x2) – x2 замещает x1. f5(x1,x2)=x2 x1
f6(x1,x2) – повтор х2. f6(x1,x2)  x2
f7(x1,x2) – сложение по модулю 2. f7(x1,x2)=x1x2
f8(x1,x2) – дизъюнкция. f8(x1,x2)=x1x2
f9(x1,x2) – стрелка Пирса (функция Вебба). f9(x1,x2)=x1x2
f10(x1,x2) – эквивалентность. f10(x1,x2)=x1x2
f11(x1,x2) – инверсия х2. f11(x1,x2)=x2
f12(x1,x2) – импликация. f12(x1,x2)=x1→x2

f13(x1,x2) – инверсия х1. f13(x1,x2)=x1
f14(x1,x2) – импликация. f14(x1,x2)=x1 → x2
f15(x1,x2) – штрих Шеффера. f15(x1,x2)=x1/x2
f16(x1,x2) – тождественная 1. f16(x1,x2)  1

х1х2=(х1х2)
3. х1х2=(х1х2)&(х1х2)
4. х1х2=(х1х2)&(х1х2)
5. х1&x2=(x1x2)
6. х1х2=х1&x2

Сочетательный закон. x1 & (x2 & x3) = (x1 &

x2) & x3; x1  (x2  x3) = (x1  x2)  x3
2. Переместительный закон. x1 & x2 = x2 & x1; x1  x2 = x2  x1
3. Распределительный закон конъюнкции относительно дизъюнкции.
x1 & (x2  x3) = (x1 & x2)  (x1 & x3)
4. Распределительный закон дизъюнкции относительно конъюнкции.
x1  (x2 & x3) = (x1  x2) & (x1  x3)

для конъюнкции

Способ доказательства (метод математической индукции):
Проверяют утверждение для конкретного n

(n=n0).
Проверяют, справедливо ли утверждение для n=n0+1
Предполагают, что утверждение справедливо для n=i.
Доказывают, что утверждение справедливо для n=i+1 (основываясь на соотношениях n=0,1,n0,n0+1 и n=i).
Если доказан п.4, то делается вывод, что утверждение справедливо для любого n≥1.

 x2 = x1&x2 Верно в соответствии с таблицей

Предположим, что

утверждение справедливо для x=i
Докажем, что утверждение справедливо для x=i+1
x1x2...xi xi+1=x1&x2&…&xi&xi+1
(x1x2...xi)xi+1=<исп. 2>(x1&x2&…&xi)&xi+1 =

= <исп.3> x1&x2&…&xi&xi+1 = <исп.1> x1&x2&…&xi&xi+1 => 5. Справедливо для
любого n≥n0.

если имеет место равенство f*(x1,x2,…,xn) = f(x1,x2,…,xn). Функция называется самодвойственной,

если она совпадает с двойственной себе функцией, то есть имеет место равенство f(x1,x2,…,xn) = f(x1,x2,…,xn).
Функция f(x1,x2,…,xn) называется линейной, если ее можно представить в виде f(x1,x2,…,xn) = C0  C1 & x1  C2 & x2 … Cn & xn ; Ci [0;1]
Функция f(x1,x2,…,xn) монотонная, если для двух наборов Х1>=X2 следует, что f(X1)=f(X2). Наборы, где Х1 и Х2 противоположны, не сравниваются.
Функция f(x1,x2,…,xn) называется симметричной, если она не меняется при произвольной нумерации аргументов.

показывает возможность выражения логических функций через 3 простейших функции: конъюнкция,

дизъюнкция, отрицание. С этого момента вся вычислительная техника базируется на этих операциях.

композиции «и», «или», «не».
f(x1,x2,…,xn)=x1&x2&…&xn&f(1,1,…,1)  x1&x2&…&xn&f(0,1,…,1)  x1&x2&…&xn&f(1,0,…,1)  x1&x2&…&xn&f(0,0,…,1)

 …  x1&x2&…&xn&f(0,0,…,0)

Способ доказательства аналогичен доказательству формулы де Моргана.

единиц в таблице истинности.
f(x1,x2,…,xn) = ((x1x2…xnf(0,0,…0)) & ((x1x2…xnf(0,0,…1)) & …

& ((x1x2…xnf(1,1,…1))
Доказательство: (метод математической индукции)
f(x1)=(x1f(1))&(x1f(0)) (n0=1)
f(x1,x2)=(x1f(0,x2))&(x1f(1,x2)) = (x1(x2f(0,0))&(x2f(0,1))&(x1(x2f(1,0))&(x2f(1,1)) = (x1f(0,0)&x2x2&f(0,1)f(0,0)&f(0,1))&(x1f(1,1)&x2x2&f(1,0)f(1,0)&f(1,1))
Предположим, что утверждение справедливо для x=i.
f(x1,x2,…,xi+1)=(xi+1f(x1,x2,…,xi,0))&(xi+1f(x1,x2,…,xi,1)) = ((x1x2…xif(0,0,…,0,0)xi+1)&(x1x2…xif(0,0,…,1,0)xi+1)& (x1x2… xi-1xif(0,0,…,1,0,0)xi+1)&…&(x1x2… xif(1,1,…,1,0)xi+1)&((x1x2…xif(0,0,…,0,1)xi+1)&(x1x2…xif(0,0,…,1,1)xi+1)& (x1x2… xi-1xif(0,0,…,1,0,1)xi+1)&…&(x1x2… xif(1,1,…,1,1)xi+1)

5. Так как п.4 доказан, то утверждение справедливо для n≥n0