Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
БАКАЛАВРСКАЯ РАБОТА Практическое применение алгоритмов раскраски планарных
Содержание
- 1. БАКАЛАВРСКАЯ РАБОТА Практическое применение алгоритмов раскраски планарных
- 2. Содержание06 Заключение22
- 3. ВведениеАктуальность темытема моей выпускной квалификационной работы связана
- 4. ВведениеОбъект исследования дипломной работы – алгоритмы раскраски
- 5. Необходимые понятияГраф G=(S,U) – этоконечное множество вершин
- 6. Необходимые понятияЕсли любые две вершины графа смежные,
- 7. Раскраска графаРаскраской вершин графа G в k
- 8. Раскраска графаОценки хроматического числа графа:χ(G)≥⌈11/6⌉ ⟹χ(G)≥1
- 9. Раскраска графаРаскраской ребер графа G в k
- 10. Алгоритмы раскраски графовВ моей работе приведено 6
- 11. Алгоритмы раскраски графовНа левом рисунке изображена логика
- 12. Алгоритмы раскраски графовДля реализации были выбраны алгоритмы
- 13. Алгоритмы раскраски графовкрасный RLFзеленый BSCсиний GREEDY |V|t,
- 14. Применение раскраски графовПрименение раскраски графов для решения
- 15. Применение раскраски графовПрименение раскраски графов для решения
- 16. Применение раскраски графовПрименение раскраски графов для решения
- 17. Применение раскраски графовТехнология электронных водяных знаковЭлектронные водяные
- 18. Применение раскраски графовТехнология нанесения водяного знака путем добавления ребер
- 19. Применение раскраски графовТехнология нанесения водяного знака путем
- 20. Применение раскраски графовТехнология нанесения водяного знака путем
- 21. Применение раскраски графовТехнология нанесения водяного знака путем
- 22. ЗаключениеВ ходе данной работы были:освещены необходимые аспекты
- 23. Спасибо за внимание! И за 4 года в Университете
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1БАКАЛАВРСКАЯ РАБОТА
Практическое применение алгоритмов раскраски
планарных графов и вопросы их
реализации
Слайд 3Введение
Актуальность темы
тема моей выпускной квалификационной работы связана
с систематизацией информации
об алгоритмах раскраски
графов, программной реализации некоторых из них и
сравнительного анализа полученных результатов.
Поскольку многие практические проблемы проще
решаются раскраской графов, чрезвычайно важны
программные реализации рассматриваемых алгоритмов,
особенно оптимальные, поэтому тема дипломной работы
является актуальной. К тому же могу отметить, что
некоторые задачи в раскраске графов до сих пор не решены,
что несомненно делает тему интересной.
Слайд 4Введение
Объект исследования дипломной работы – алгоритмы раскраски
планарных графов и
их практическое применение.
Предмет исследования – характеристики эффективности алгоритмов,
области применения
алгоритмов раскраски графов.Цель работы – программная реализация и сравнительный анализ
алгоритмов раскраски графов, определение области их практического
применения.
Задачи работы:
Рассмотреть основные понятия теории графов
Рассмотреть основные понятия и теоремы раскраски графов
Рассмотреть алгоритмы раскраски графов
Реализовать алгоритмы программно
Провести сравнительный анализ реализованных алгоритмов
Описать практические способы применения раскраски графов
Слайд 5Необходимые понятия
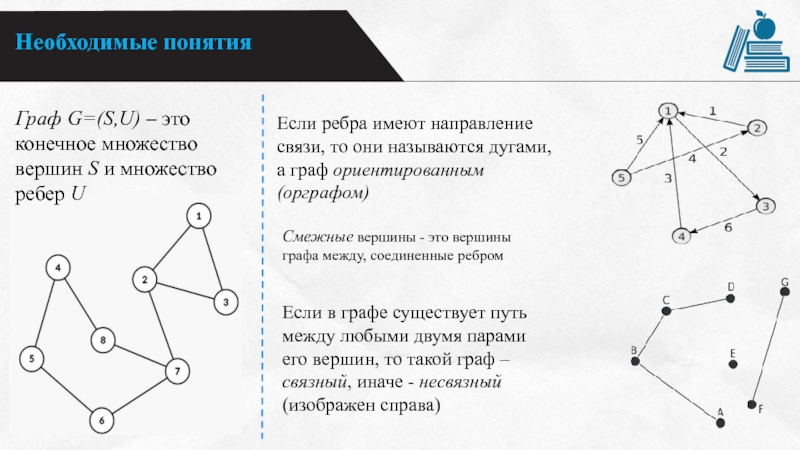
Граф G=(S,U) – это
конечное множество
вершин S и множество
ребер U
Если ребра имеют направление
связи, то они называются дугами,
а граф ориентированным
(орграфом)
Смежные вершины - это вершины
графа между, соединенные ребром
Если в графе существует путь
между любыми двумя парами
его вершин, то такой граф –
связный, иначе - несвязный
(изображен справа)
Слайд 6Необходимые понятия
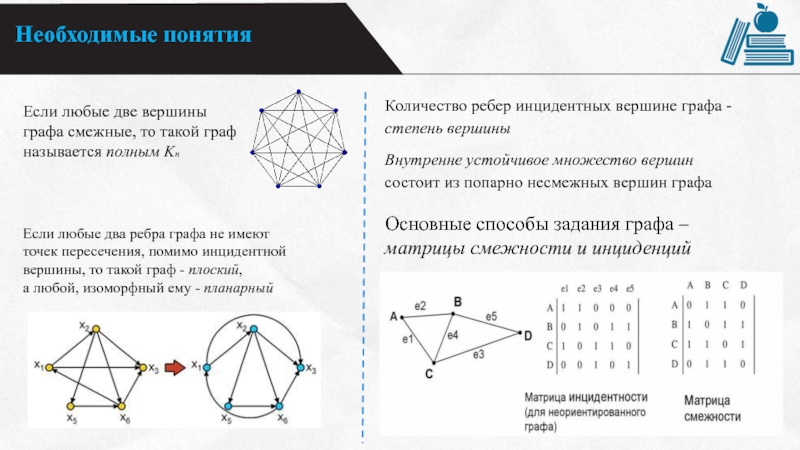
Если любые две вершины графа смежные, то такой граф
называется полным Kn
Если любые два ребра графа не имеют
точек
пересечения, помимо инцидентной вершины, то такой граф - плоский, а любой, изоморфный ему - планарный
Количество ребер инцидентных вершине графа - степень вершины
Основные способы задания графа –
матрицы смежности и инциденций
Внутренне устойчивое множество вершин
состоит из попарно несмежных вершин графа
Слайд 7Раскраска графа
Раскраской вершин графа G в k цветов называется функция
ρ:V(G)→M, где
|M|=k. Раскраска ρ называется правильной, если ρ(v)≠ρ(u) для
любой пары смежных вершин u и v
χ(G) - хроматическое число графа G – наименьшее натуральное число, для которого
существует правильная раскраска вершин графа G в такое количество цветов
На данный момент не существует точной формулы для расчета хроматического
числа графа, но существуют оценки для него, позволяющие определить интервал
значений
k-раскрашиваемый граф - граф, который можно правильно раскрасить в k цветов
Теорема о пяти красках: любой планарный граф можно правильно раскрасить в 5 цветов.
Появилась на основе гипотезы о четырех красках, которая была доказана только для случаев,
когда вершин в графе не более 38, - это самая известная проблема раскраски графов, имеющая
долгую историю попыток доказать ее истинность
Слайд 8Раскраска графа
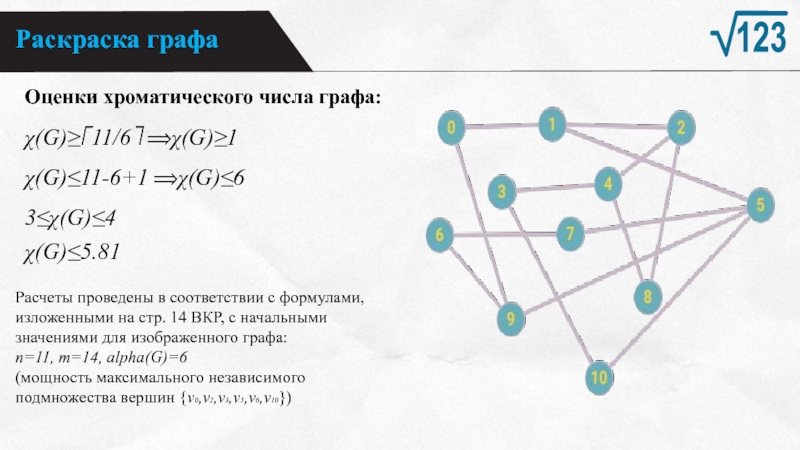
Оценки хроматического числа графа:
χ(G)≥⌈11/6⌉ ⟹χ(G)≥1
χ(G)≤11-6+1 ⟹χ(G)≤6
3≤χ(G)≤4
χ(G)≤5.81
Расчеты
проведены в соответствии с формулами, изложенными на стр. 14 ВКР,
с начальнымизначениями для изображенного графа:
n=11, m=14, alpha(G)=6
(мощность максимального независимого
подмножества вершин {v0,v2,v3,v5,v6,v10})
Слайд 9Раскраска графа
Раскраской ребер графа G в k цветов называется функция
ρ:E(G)→M, где
|M|=k. Раскраска ρ называется правильной, если ρ(e)≠ρ(e') для
любой пары смежных ребер e и e’
χ'(G) – реберное хроматическое число или хроматический индекс графа G –
наименьшее натуральное число, для которого существует правильная
раскраска ребер графа G в такое количество цветов
Теорема Визинга для графов, допускающих кратные ребра:
пусть граф G – граф без петель. Тогда χ'(G)≤ Δ(G)+μ(G). Где Δ(G) - максимальная из степеней вершин графа, μ(G) - максимальная кратность ребер в графе
Раскраска ребер связана с вершинной раскраской графа, и смогла дополнить гипотезу о четырех красках, доказав теорему: для того чтобы хроматическое число графа было
равно 4, необходимо и достаточно, чтобы его ребра допускали такую раскраску в три
цвета, при которой никакие два ребра одной грани не были раскрашены одинаково
Слайд 10Алгоритмы раскраски графов
В моей работе приведено 6 общих алгоритмов раскраски
(и определения
хроматического числа) графов и один частный алгоритм (Виндерсона),
которыйпозволяет оптимально раскрасить граф, зная его хроматическое число
Все алгоритмы кроме последнего, можно разделить на группы:
точные алгоритмы (Вейсманна, Лорьера-Новикова)
эвристические алгоритмы поиска правильной раскраски (жадный, перебор, рекурсивный)
Так же заметно, что все эвристические алгоритмы, кроме жадного, основаны
либо на поиске независимых подмножеств вершин графа, либо на
предварительном перед жадным способом раскраски упорядочивании вершин
Слайд 11Алгоритмы раскраски графов
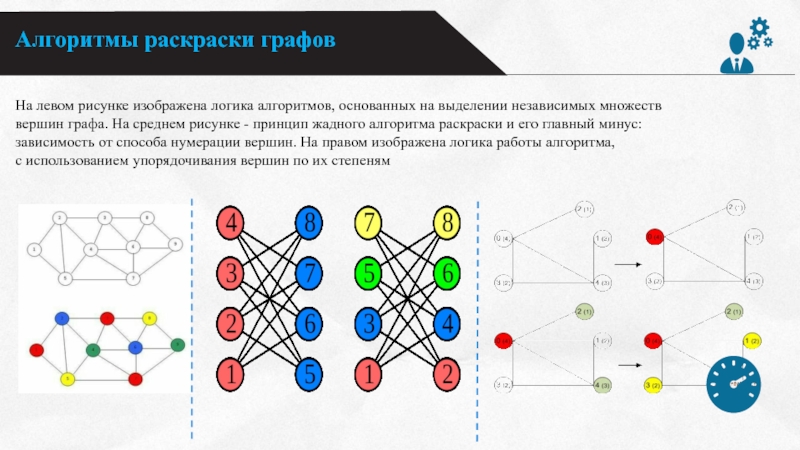
На левом рисунке изображена логика алгоритмов, основанных на
выделении независимых множеств
вершин графа. На среднем рисунке - принцип
жадного алгоритма раскраски и его главный минус: зависимость от способа нумерации вершин. На правом изображена логика работы алгоритма,
с использованием упорядочивания вершин по их степеням
Слайд 12Алгоритмы раскраски графов
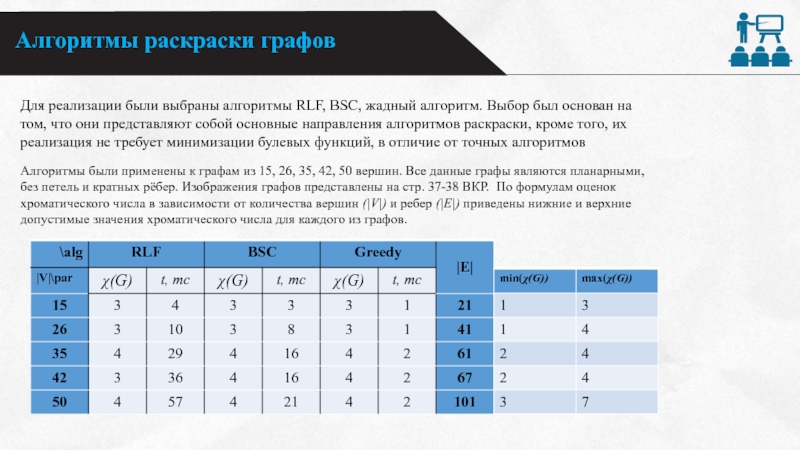
Для реализации были выбраны алгоритмы RLF, BSC, жадный
алгоритм. Выбор был основан на
том, что они представляют собой
основные направления алгоритмов раскраски, кроме того, их реализация не требует минимизации булевых функций, в отличие от точных алгоритмов
Алгоритмы были применены к графам из 15, 26, 35, 42, 50 вершин. Все данные графы являются планарными,
без петель и кратных рёбер. Изображения графов представлены на стр. 37-38 ВКР. По формулам оценок
хроматического числа в зависимости от количества вершин (|V|) и ребер (|E|) приведены нижние и верхние
допустимые значения хроматического числа для каждого из графов.
Слайд 13Алгоритмы раскраски графов
красный RLF
зеленый BSC
синий GREEDY
|V|
t, mc
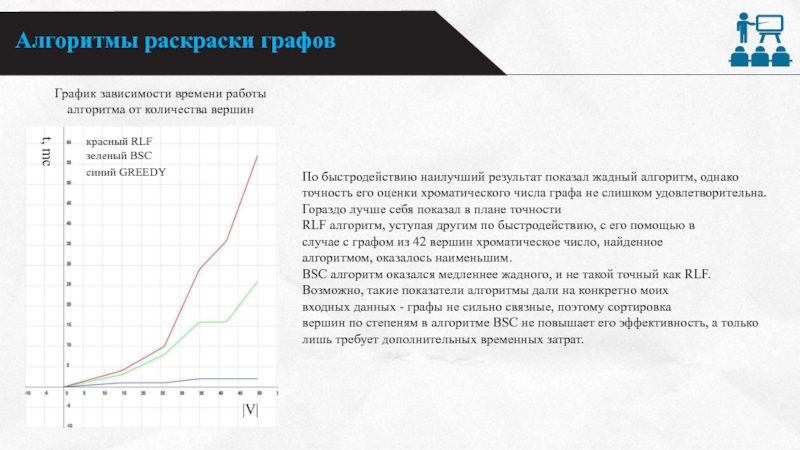
График зависимости
времени работы алгоритма от количества вершин
По быстродействию наилучший результат показал
жадный алгоритм, однако точность его оценки хроматического числа графа не слишком удовлетворительна. Гораздо лучше себя показал в плане точности RLF алгоритм, уступая другим по быстродействию, с его помощью в
случае с графом из 42 вершин хроматическое число, найденное
алгоритмом, оказалось наименьшим.
BSC алгоритм оказался медленнее жадного, и не такой точный как RLF.
Возможно, такие показатели алгоритмы дали на конкретно моих
входных данных - графы не сильно связные, поэтому сортировка
вершин по степеням в алгоритме BSC не повышает его эффективность, а только лишь требует дополнительных временных затрат.
Слайд 14Применение раскраски графов
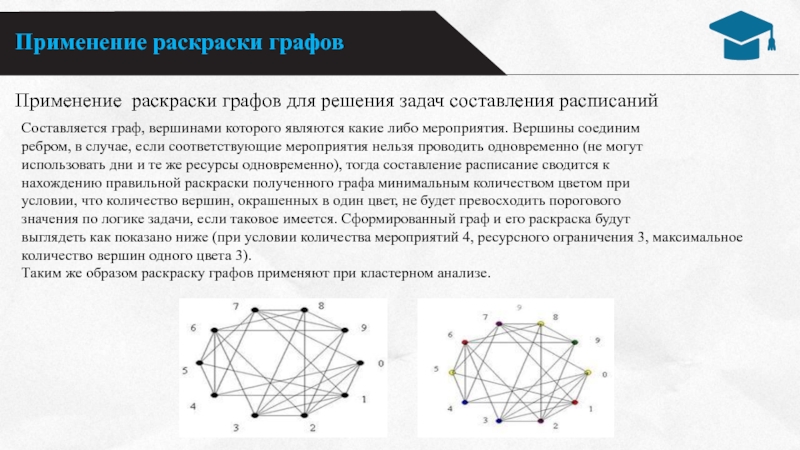
Применение раскраски графов для решения задач составления расписаний
Составляется
граф, вершинами которого являются какие либо мероприятия. Вершины соединим
ребром,
в случае, если соответствующие мероприятия нельзя проводить одновременно (не могут использовать дни и те же ресурсы одновременно), тогда составление расписание сводится к
нахождению правильной раскраски полученного графа минимальным количеством цветом при
условии, что количество вершин, окрашенных в один цвет, не будет превосходить порогового
значения по логике задачи, если таковое имеется. Сформированный граф и его раскраска будут
выглядеть как показано ниже (при условии количества мероприятий 4, ресурсного ограничения 3, максимальное количество вершин одного цвета 3).
Таким же образом раскраску графов применяют при кластерном анализе.
Слайд 15Применение раскраски графов
Применение раскраски графов для решения задач распределения частот
Если
представить карту вышек сотовой связи в виде графа, то вершинами
его будут зоны покрытиявышек, а смежными они будут, только если имеют общую границу и перекрываются. Станции, в
таком случае, не могу работать на одной частоте, из-за помех. Один цвет (color class) представляет
один диапазон частот. Тогда, любая правильная раскраска графа обеспечит функционирование сети
без помех, и хроматическое число определяет наименьшее количество диапазонов частот для
бесперебойной работы сети.
Используется алгоритм основанный на выделении независимых подмножеств вершин.
Слайд 16Применение раскраски графов
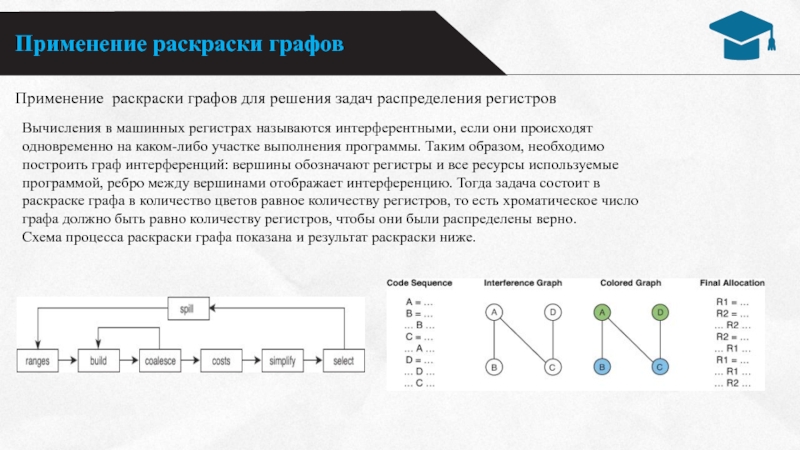
Применение раскраски графов для решения задач распределения регистров
Вычисления
в машинных регистрах называются интерферентными, если они происходят
одновременно на
каком-либо участке выполнения программы. Таким образом, необходимо построить граф интерференций: вершины обозначают регистры и все ресурсы используемые
программой, ребро между вершинами отображает интерференцию. Тогда задача состоит в
раскраске графа в количество цветов равное количеству регистров, то есть хроматическое число
графа должно быть равно количеству регистров, чтобы они были распределены верно.
Схема процесса раскраски графа показана и результат раскраски ниже.
Слайд 17Применение раскраски графов
Технология электронных водяных знаков
Электронные водяные знаки наносятся на
программное обеспечение с целью защиты
интеллектуальной собственности. Суть их состоит
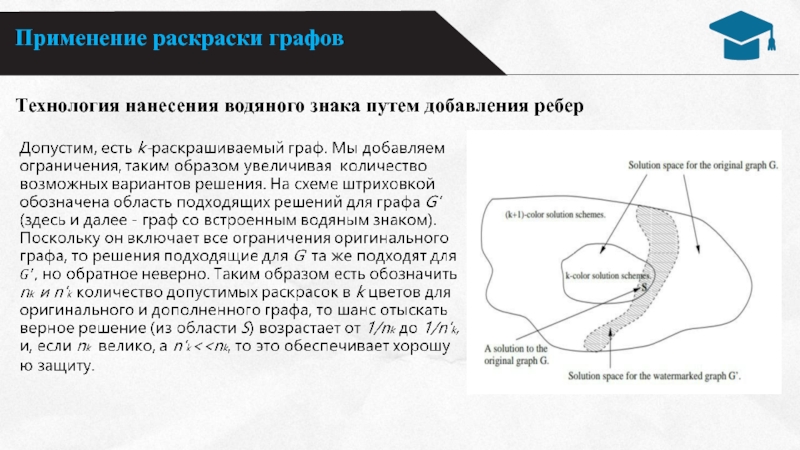
не в добавлении какого либо кода в программу, а в переводе подписи автора в множество дополнительных ограничений, которые добавляются в оригинал ПО. Так как такая подпись основана на добавлении ограничений, то возможно некоторое ухудшение качества самого ПО. Поэтому необходимо держать баланс между степенью надежности защиты и степенью снижения качества ПО.
Раскраска графов применяется в так называемой constraint-based (основанной на ограничениях)
технологии нанесения электронного водяного знака. Исследования показали, что даже огромный
объем информации водяного знака может быть внедрен в граф, и при этом хроматическое число
графа, с водяным знаком будет отличаться не более, чем на 1. И даже практически все графы с
большим дополнительным объемом информации о водяном знаке могут быть раскрашены в
известное число цветов оригинального графа, без увеличения временных затрат.
Далее будут изложены три различных подхода к кодированию электронной подписи с помощью
алгоритмов раскраски графа.
Слайд 19Применение раскраски графов
Технология нанесения водяного знака путем добавления ребер
Процесс нанесения
водяного знака:
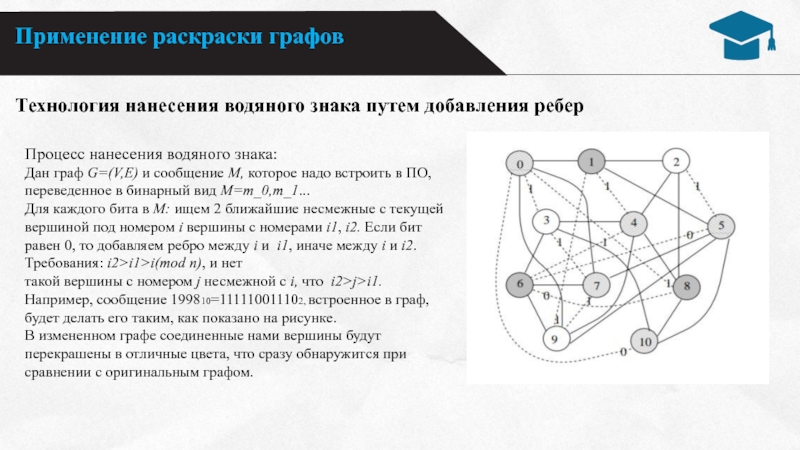
Дан граф G=(V,E) и сообщение М, которое надо встроить
в ПО, переведенное в бинарный вид M=m_0,m_1...Для каждого бита в М: ищем 2 ближайшие несмежные с текущей вершиной под номером i вершины с номерами i1, i2. Если бит равен 0, то добавляем ребро между i и i1, иначе между i и i2. Требования: i2>i1>i(mod n), и нет
такой вершины с номером j несмежной с i, что i2>j>i1.
Например, сообщение 199810=111110011102, встроенное в граф, будет делать его таким, как показано на рисунке.
В измененном графе соединенные нами вершины будут перекрашены в отличные цвета, что сразу обнаружится при сравнении с оригинальным графом.
Слайд 20Применение раскраски графов
Технология нанесения водяного знака путем поиска независимых подмножеств
вершин графа
Процесс нанесения водяного знака:
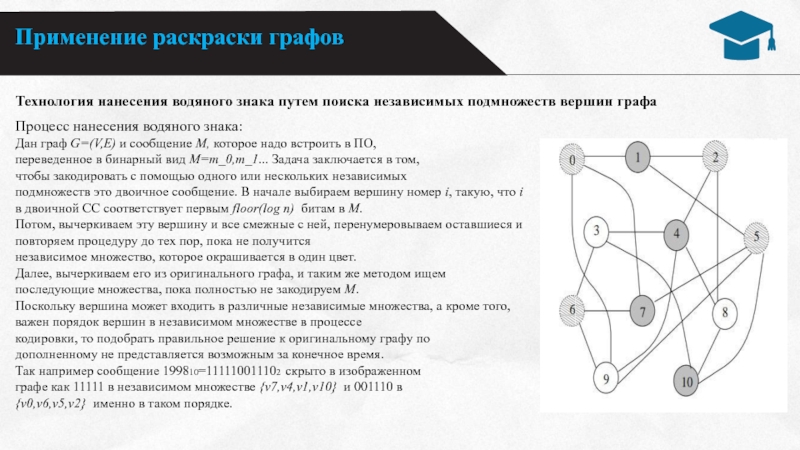
Дан граф G=(V,E) и сообщение
М, которое надо встроить в ПО, переведенное в бинарный вид M=m_0,m_1... Задача заключается в том,
чтобы закодировать с помощью одного или нескольких независимых
подмножеств это двоичное сообщение. В начале выбираем вершину номер i, такую, что i в двоичной СС соответствует первым floor(log n) битам в М.
Потом, вычеркиваем эту вершину и все смежные с ней, перенумеровываем оставшиеся и повторяем процедуру до тех пор, пока не получится
независимое множество, которое окрашивается в один цвет.
Далее, вычеркиваем его из оригинального графа, и таким же методом ищем
последующие множества, пока полностью не закодируем М.
Поскольку вершина может входить в различные независимые множества, а кроме того, важен порядок вершин в независимом множестве в процессе
кодировки, то подобрать правильное решение к оригинальному графу по
дополненному не представляется возможным за конечное время.
Так например сообщение 199810=111110011102 скрыто в изображенном
графе как 11111 в независимом множестве {v7,v4,v1,v10} и 001110 в
{v0,v6,v5,v2} именно в таком порядке.
Слайд 21Применение раскраски графов
Технология нанесения водяного знака путем добавления вершин и
ребер
Процесс нанесения водяного знака:
Дан граф G=(V,E) и сообщение М,
которое надо встроить в ПО, переведенное в бинарный вид M=m_0,m_1... Затем, мы объявляем новую вершину v, и соединяем ее с вершиной соответствующей первым floor(log n) битам в М. Далее, соединяем с вершинами соответствующими floor(log n – i*1)
битам М. Если одной вершины оказалось мало, то добавляем еще одну и действуем по такому же
принципу, пока М не будет полностью закодировано.
Выявить наличие такого водяного знака крайне трудно, так как невозможно определить какие из
вершин были добавлены.
Рассмотренный в работе QP алгоритм нанесения водяного знака и его модификации
базируются на первой изложенной технологии, собственно, сам базовый QP алгоритм описывает по шагам основные идеи первого метода – добавления ребер.
Слайд 22Заключение
В ходе данной работы были:
освещены необходимые аспекты теории графов
описаны алгебраические
основы раскраски графов
рассмотрены алгоритмы раскраски графов и три из них
реализованы в среде Microsoft Visual Studio 2017
был проведен анализ полученных результатов работы реализованных алгоритмов
широко освещена тема прикладного использования раскраски графов
подробно разобрана технология нанесения цифровых водяных знаков






























![АВТОМАТИЗАЦИЯ ЗВУКА [ Л ]
В СЛОВАХ](/img/tmb/6/598195/9904114927fd66f267234b3a5c44ea6c-800x.jpg)
