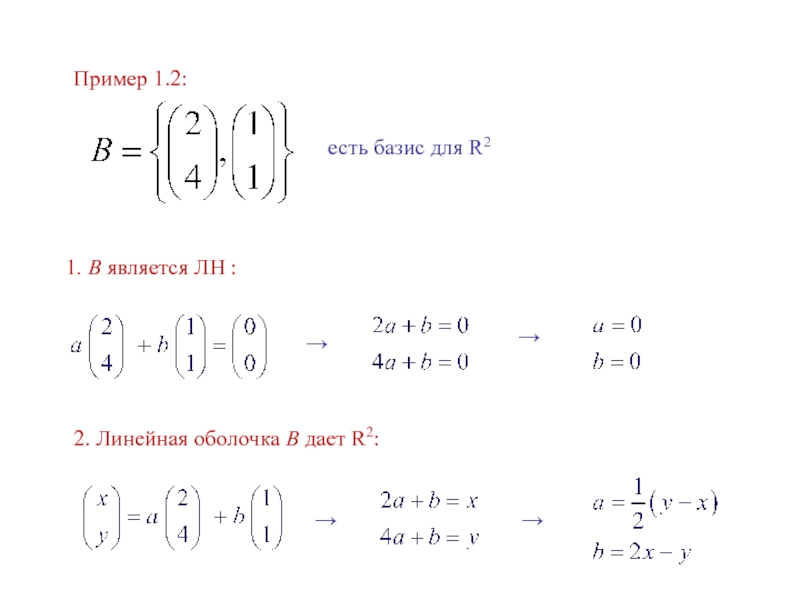Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
базис и размерность
Содержание
- 1. базис и размерность
- 2. 1.Базис(или база)Определение 1.1: БазисБазиcом векторного пространства V
- 3. Пример 1.2:есть базис для R21. B является ЛН :→→2. Линейная оболочка B дает R2:→→
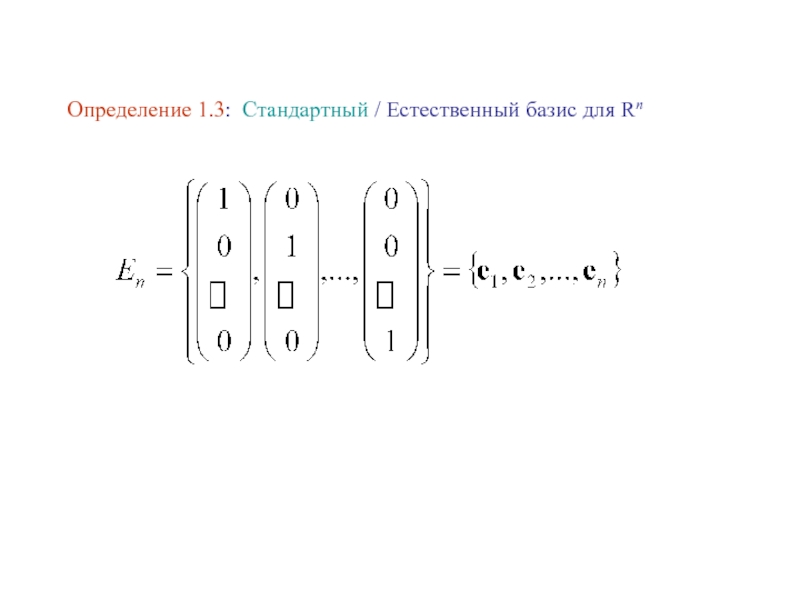
- 4. Определение 1.3: Стандартный / Естественный базис для Rn
- 5. Теорема 1.4:Для всякого векторного пространства, подмножество является
- 6. Приведем геометрическую интерпретацию координат вектора. Пусть геометрический
- 7. Определение 1.5: Разложение по базисуПусть задан базис
- 8. 2. РазмерностьОпределение 2.1 Векторное пространство называется конечномерным,
- 9. Теорема 2.3: Для любого конечномерного пространства, все
- 10. Определение 2.4: РазмерностьРазмерность векторного пространства есть число
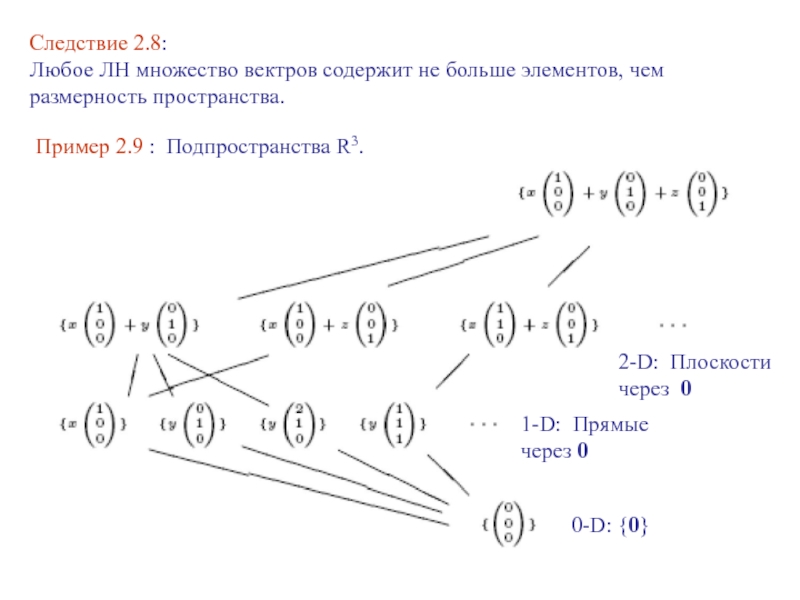
- 11. Следствие 2.8:Любое ЛН множество вектров содержит не
- 12. Следствие 2.10:Любое ЛН множество векторов может быть
- 13. 3. Матрица перехода от одного базиса к
- 14. Слайд 14
- 15. Доказательство. Пусть Р – матрица перехода от
- 16. Возьмем произвольный вектор
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 21.Базис(или база)
Определение 1.1: Базис
Базиcом векторного пространства V называтся упорядоченное множество
линейно независимых (ненулевых) векторов, линейная оболочка которых дает V.
Слайд 5Теорема 1.4:
Для всякого векторного пространства, подмножество является базисом тогда и
только тогда, когда каждый вектор пространства можно выразить единственным образом
в виде линейной комбинации элементов подмножества.Доказательство: По определению линейной оболочки
→ каждый вектор можно выразить в виде линейной комбинации базисных векторов. Пусть такое представление не единственно:
Но
тогда
- ЛН система ⇔
QED
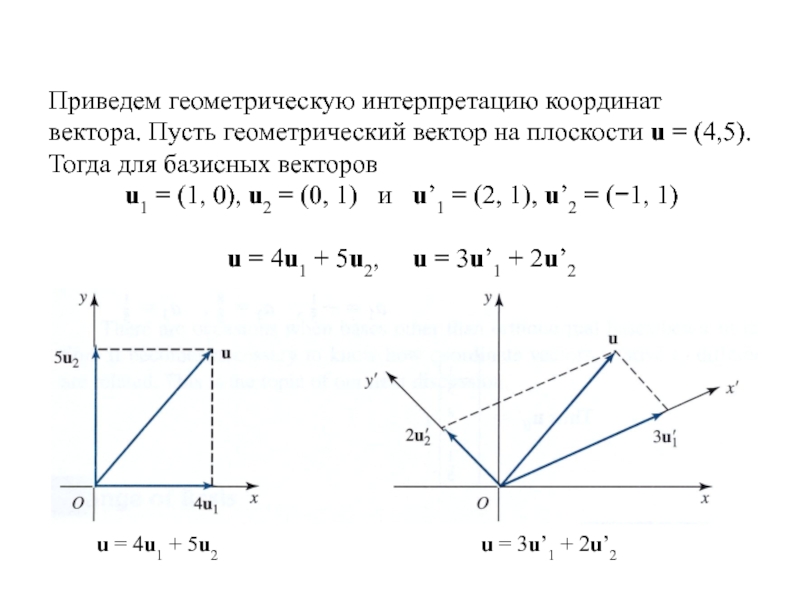
Слайд 6Приведем геометрическую интерпретацию координат вектора. Пусть геометрический вектор на плоскости
u = (4,5). Тогда для базисных векторов
u1 = (1, 0),
u2 = (0, 1) и u’1 = (2, 1), u’2 = (−1, 1)u = 4u1 + 5u2, u = 3u’1 + 2u’2
Слайд 7Определение 1.5: Разложение по базису
Пусть задан базис B =
векторного пространства V ,тогда
называют разложением вектора v по базе B.
Разложение также можно задать столбцом
cj называются координатами(компонентами) v в B.
Пример 1.6:
Пусть
Тогда координаты элемента
Слайд 82. Размерность
Определение 2.1
Векторное пространство называется конечномерным, если оно имеет
базу из конечного числа векторов.
Лемма 2.2: Лемма о замене
базисного элемента Предположим, что является базисом векторного пространства и для вектора v выполняется соотношение:
Тогда, заменив bj на v, получим другой базис пространства.
причем cj ≠ 0.
Доказательство: Действительно, является ЛН системой и для произвольного вектора
QED
Слайд 9Теорема 2.3:
Для любого конечномерного пространства, все базисы имеют одинаковое
число элементов.
Доказательство:
Пусть
есть базис из n элементов.Возьмем другой базис { g1 , …, gm }, предположим m ≥ n.
Пусть
и ck ≠ 0.
По лемме 2.2, { b1 , …, bk − 1 ,g1 ,bk + 1 , …, bn } также есть базис.
Далее, заменив для некоторого j bj на g2 , получим новый базис { b1 , …, bk − 1 ,g1 ,bk + 1 , …, bj − 1 ,g2 ,bj + 1 , …, bn }.
Продолжая процесс n раз, получим базис { g1 , …, gn }.
Это противоречит тому, что { g1 , …, gm } − ЛН.
Причем хотя бы один из коэффициентовck ≠ 0.
Предпололжим m > n, тогда
Поэтому m = n.
Слайд 10Определение 2.4: Размерность
Размерность векторного пространства есть число векторов в любом
из его базисов. ( Обозначение dim V)
Пример 2.5:
Пространство n-разрядных столбцов Rn .Любой базис пространства Rn содержит n векторов, так как его стандартный базис Еn содержит n векторов.
→ dim Rn = n .
Пример 2.6: Пространство Pn многочленов степени не выше n
dim P = n+1, так как его натуральный базис { 1, x, x2, …, xn }, содержит n+1 элемент.
Пример 2.7:
Тривиальное пространство является 0-мерным , так как его базис пуст.
Слайд 11Следствие 2.8:
Любое ЛН множество вектров содержит не больше элементов, чем
размерность пространства.
Пример 2.9 : Подпространства R3.
2-D: Плоскости через 0
1-D: Прямые
через 00-D: {0}
Слайд 12Следствие 2.10:
Любое ЛН множество векторов может быть расширено до базиса.
Следствие
2.11:
Любой набор S, такой что span S = V,
можно сузить до базиса.Следствие 2.12:
В n-мерном векторном пространстве, множество S из n векторов является ЛН т.и т.т.к. span S = V.
Слайд 133. Матрица перехода от одного базиса к другому
Пусть даны два
базиса В =
и G = векторного пространства V. Тогда элементы второго базиса можно выразить через первый базис:Или, в матричном виде:
Определение 3.1: Матрица Р называется матрицей перехода от базиса B к базису G.
Слайд 15Доказательство. Пусть Р – матрица перехода от базиса В к
базису G:
Точно также можно найти матрицу перехода от базиса G к базису В, пусть R- матрица перехода:
.
Тогда из последних двух соотношений получим
Так как В и G – ЛН системы, получим PR = RP = I. Таким образом R – обратная матрица к Р и Р – невырождена.
QED
Теорема 3.2: Матрица Р перехода от базиса В к базису G является невырожденной. Матрица перехода от G к B равна .
Слайд 16Возьмем произвольный вектор
и два базиса В =
и G = векторного пространства V. Разложим вектор v по этим базисам:Тогда:
Из сравнения получим , или в матричном виде:
- связь координат одного и того же вектора в различных базах.