Слайд 1Методы оптимизации
8.ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Слайд 28.1. ВВЕДЕНИЕ
Целочисленное линейное программирование (ЦЛП) ориентировано на решение
задач линейного программирования, в которых все или некоторые переменные должны
принимать целочисленные (или дискретные) значения. Несмотря на интенсивные исследования, проводимые на протяжении последних десятилетий, известные вычислительные методы решения задач ЦЛП далеки от совершенства. На сегодня не существует надежных вычислительных алгоритмов решения таких задач.
В настоящей главе рассматриваются сначала примеры задач целочисленного программирования, а затем методы их решения.
Слайд 36.2. ПРИМЕРЫ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
Рассмотрим сначала простые практические
задачи, которые сводятся к задачам ЦЛП, затем обратимся к более
сложным. Для удобства задачи, в которых все переменные должны быть целочисленными, называются полностью целочисленными, а задачи, в которых лишь некоторые переменные должны принимать целочисленные значения, — частично-целочисленными.
Пример 6.2-1. (Распределение капиталовложений)
Оценивается пять проектов с точки зрения их возможного финансирования на предстоящий трехлетний период. Следующая таблица содержит ожидаемую прибыль от реализации каждого проекта и распределение необходимых капиталовложений по годам.
Предполагается, что каждый утвержденный проект будет реализован за трехлетний период. Необходимо определить совокупность проектов, которой соответствует максимум суммарной прибыли.
Задача сводится к решению типа "да - нет" относительно каждого проекта. Определим двоичные переменные хj:
Слайд 4 Задача ЦЛП будет записана следующим образом.
Максимизировать
z = 20х1 + 40х2 + 20х3 +
15х4 + 30х5
при ограничениях
5x1 + 4х2 + 3х3 + 7х4 + 8х5 ≤ 25,
х1 + 7х2 + 9х3 + 4х4 + 6x5 ≤ 25,
8x1 + 10х2 + 2х3 + x4 + 10x5 ≤ 25,
х1, х2, х3, х4, x5 = 0 или 1.
Оптимальным целочисленным решением является х1 = х2 = х3 = х4 = 1, х5 = 0 с z = 95 (млн. долл.). Это решение означает, что необходимо выбрать для финансирования все проекты, кроме пятого.
Интересно сравнить решение данной задачи ЦЛП с решением "обычной" задачи ЛП с теми же ограничениями, но без условия целочисленности переменных. Задача линейного программирования получается в результате замены условия хj = 0 или 1 на ограничение 0 ≤ хj ≤ 1 для всех j. Эта задача имеет решение х1 = 0.5789, х2 = х3 = х4 = 1, х5 = 0.7368 и z = 108.68 (млн. долл.). Такое решение с точки зрения целочисленной задачи лишено смысла, так как две переменные принимают дробное значение. Можно было бы попытаться округлить полученный результат, что привело бы к х1 = х5 = 1. Полученное при этом решение является недопустимым, так как нарушаются ограничения задачи. Более существенным в этой ситуации является то, что округление применять нельзя, так как хj представляет решение типа "да - нет", для которого дробные значения лишены смысла.

Слайд 58.3.МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
Методы решения задач
целочисленного линейного программирования основаны на использовании вычислительных возможностей методов линейного
программирования. Обычно алгоритмы целочисленного программирования включают три шага.
Шаг 1. "Ослабление" пространства допустимых решений задачи целочисленного линейного программирования путем замены любой двоичной переменной y непрерывным ограничением 0 ≤ у ≤ 1 и отбрасывания требования целочисленности для всех остальных переменных. В результате получается обычная задача линейного программирования.
Шаг 2. Решение задачи линейного программирования и определение ее оптимального решения.
Шаг 3. Имея полученное (непрерывное) оптимальное решение, добавляем специальные ограничения, которые итерационным путем изменяют пространство допустимых решений задачи линейного программирования таким образом, чтобы, в конечном счете, получилось оптимальное решение, удовлетворяющее требованиям целочисленности.
Разработаны два общих метода генерирования специальных ограничений, о которых идет речь при реализации шага 3.
Метод ветвей и границ.
Метод отсекающих плоскостей.
Хотя ни один из упомянутых методов не дает надежных результатов при решении задачи целочисленного линейного программирования, опыт вычислений свидетельствует, что метод ветвей и границ более успешно решает задачу, чем метод отсекающих плоскостей.

Слайд 6 Метод ветвей и границ
Основы этого
метода объясним на численном примере.
Пример 6.3-1
Рассмотрим следующую задачу целочисленного линейного программирования.
Максимизировать
z = 5х1 + 4х2
при ограничениях
х1 + х2 ≤ 5,
10x1 + 6х2 ≤ 45,
х1, х2 ≥ 0 и целые.
На рис. 6.6 пространство допустимых решений задачи целочисленного линейного программирования представлено точками. Соответствующая начальная задача линейного программирования (обозначим ее ЛП0) получается путем отбрасывания условий целочисленности. Ее оптимальным решением будет х1 = 3.75, х2= 1.25 и z = 23.75.
Рис. 6.6
Слайд 7 Так как оптимальное решение задачи ЛП0 не
удовлетворяет условия целочисленности, метод ветвей и границ изменяет пространство решений
задачи линейного программирования так, что, в конечном счете, получается оптимальное решение задачи целочисленного линейного программирования. Для этого сначала выбирается одна из целочисленных переменных, значение которой в оптимальном решении задачи ЛП0 не является целочисленным. Например, выбирая х1 (= 3.75), замечаем, что область 3 < х1 < 4 пространства допустимых решений задачи ЛП0 не содержит целочисленных значений переменной х1 и, следовательно, может быть исключена из рассмотрения, как бесперспективная. Это эквивалентно замене исходной задачи ЛП0 двумя новыми задачами линейного программирования ЛП1 и ЛП2, которые определяются следующим образом:
пространство допустимых решений ЛП1 = пространство допустимых решений ЛП0 + (х1 ≤ 3),
пространство допустимых решений ЛП2 = пространство допустимых решений ЛП0 + (х1 ≥ 4).
На рис. 6.7 изображены пространства допустимых решений задач ЛП1 и ЛП2. Оба пространства содержат все допустимые решения исходной задачи ЦЛП. Это означает, что задачи ЛП1 и ЛП2 "не потеряют" решения начальной задачи ЛП0.
Рис. 6.7

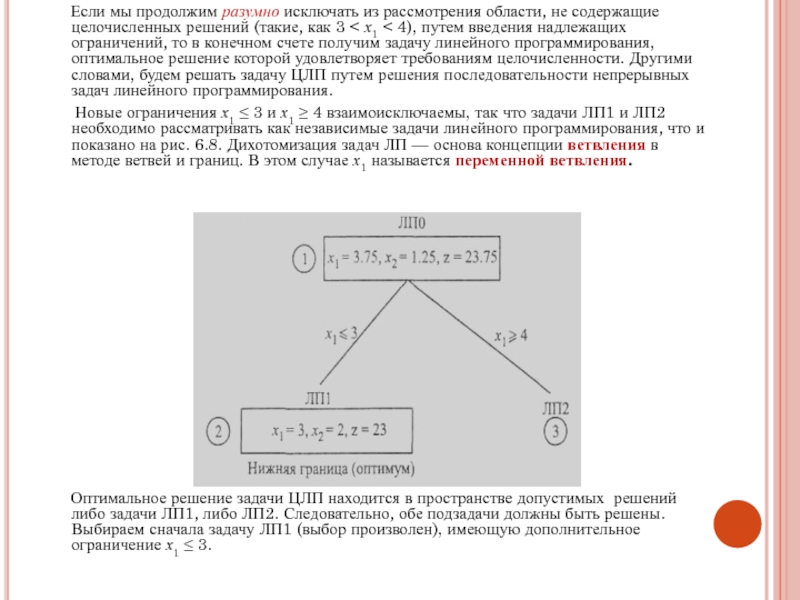
Слайд 8 Если мы продолжим разумно исключать из рассмотрения
области, не содержащие целочисленных решений (такие, как 3 < х1
< 4), путем введения надлежащих ограничений, то в конечном счете получим задачу линейного программирования, оптимальное решение которой удовлетворяет требованиям целочисленности. Другими словами, будем решать задачу ЦЛП путем решения последовательности непрерывных задач линейного программирования.
Новые ограничения х1 ≤ 3 и х1 ≥ 4 взаимоисключаемы, так что задачи ЛП1 и ЛП2 необходимо рассматривать как независимые задачи линейного программирования, что и показано на рис. 6.8. Дихотомизация задач ЛП — основа концепции ветвления в методе ветвей и границ. В этом случае х1 называется переменной ветвления.
Рис. 6.8
Оптимальное решение задачи ЦЛП находится в пространстве допустимых решений либо задачи ЛП1, либо ЛП2. Следовательно, обе подзадачи должны быть решены. Выбираем сначала задачу ЛП1 (выбор произволен), имеющую дополнительное ограничение х1 ≤ 3.
Максимизировать z = 5х1 + 4х2
при ограничениях
х1 + х2 ≤ 5,
10x1 + 6х2 ≤ 45,
х1 ≤ 3,
х1, х2 ≥ 0.
Оптимальным решением задачи ЛП1 (которое можно получить с помощью метода решения задач с ограниченными переменными, изложенного в разделе 7.5.2) является х1 = 3, х2 = 2 и z = 23.
Оптимальное решение задачи ЛП1 удовлетворяет требованию целочисленности переменных х1 и х2. В этом случае говорят, что задача ЛП1 прозондирована. Это означает, что задача ЛП1 не должна больше зондироваться, так как она не может содержать лучшего решения задачи ЦЛП.
Мы не можем в этой ситуации оценить качество целочисленного решения, полученного из рассмотрения задачи ЛП1, ибо решение задачи ЛП2 может привести к лучшему целочисленному решению (с большим значением целевой функции z). Пока мы можем лишь сказать, что значение z = 23 является нижней границей оптимального (максимального) значения целевой функции исходной задачи ЦЛП. Это значит, что любая нерассмотренная подзадача, которая не может привести к целочисленному решению с большим значением целевой функции, должна быть исключена из рассмотрения, как бесперспективная. Если же нерассмотренная подзадача может привести к лучшему целочисленному решению, то нижняя граница должна быть надлежащим образом изменена.
При значении нижней границы z = 23 исследуем задачу ЛП2 (единственную оставшуюся нерассмотренную подзадачу). Так как в задаче ЛП0 оптимальное значение целевой функции равно 23.75 и все ее коэффициенты являются целыми числами, то невозможно получить целочисленное решение задачи ЛП2 (пространство решений которой более узко, чем в задаче ЛП0), которое будет лучше имеющегося. В результате мы отбрасываем подзадачу ЛП2 и считаем ее прозондированной.
Реализация метода ветвей и границ завершена, так как обе подзадачи ЛП1 и ЛП2 прозондированы (рассмотрение первой привело к нахождению целочисленного решения, а второй — к заключению, что ее возможное целочисленное решение не может быть лучше имеющегося). Следовательно, мы заключаем, что оптимальным решением задачи ЦЛП является решение, соответствующее нижней границе, а именно х1 = 3, х2 = 2 и z = 23.

Слайд 10 Остались без ответа два вопроса, связанные с
реализацией описанной вычислительной процедуры.
Можно ли было в
задаче ЛП0 выбрать переменную х2 в качестве переменной ветвления вместо х1?
Можно ли было при выборе подзадачи для зондирования решить сначала задачу ЛП2 вместо ЛП1?
Ответы на оба вопроса положительные. Однако последующие вычисления могут значительно отличаться.
Последовательность решения подзадач, показанная на рис. 6.9 (ЛП0, ЛП2, ЛП4, ЛП3, ЛП6, ЛП5, ЛП1), является наихудшей; тем не менее, она встречается на практике. Этот пример указывает на основную слабость метода ветвей и границ: как выбирать следующую подзадачу для исследования и как выбирать для нее переменную ветвления?
В процессе решения, представленного на рис. 6.8, мы случайно наткнулись на хорошую нижнюю границу значений целевой функции на самой первой подзадаче ЛП1, что позволило прозондировать ЛП2 без детальных исследований и закончить вычисления. По существу, мы завершили вычисления, решив лишь одну подзадачу. В процессе решения, представленном на рис. 6.9, мы были вынуждены исследовать семь подзадач, и лишь тогда завершились вычисления метода ветвей и границ. Хотя имеются эвристические соображения, позволяющие "угадать", какая из ветвей может привести к улучшенному решению задачи ЦЛП, не существует строгой теории, которая всегда обеспечивала бы надежные результаты.
Теперь сформулируем алгоритм метода ветвей и границ в общем случае. Предположим, что рассматривается задача максимизации. Зададим нижнюю границу оптимального значения целевой функции z задачи ЦЛП равной -∞. Положим i = 0.

Слайд 11 Шаг 1. (Зондирование и определение границы). Выбираем
i-ю подзадачу линейного программирования ЛПi для исследования. Решаем ЛПi и
зондируем ее, при этом возможна одна из трех ситуаций.
а) Оптимальное значение целевой функции задачи ЛПi не может улучшить текущей нижней границы.
b) ЛПi приводит к лучшему допустимому целочисленному решению, чем текущая нижняя граница.
с) ЛПi не имеет допустимых решений.
Возможны два случая.
а) Если задача ЛПi прозондирована, нижняя граница изменяется только при условии, что найдено лучшее решение задачи ЦЛП. Если все подзадачи прозондированы, необходимо закончить вычисления: оптимальным решением задачи ЦЛП является то, которое соответствует текущей нижней границе, если такая существует. Иначе положить i = i + 1 и повторить шаг 1.
b) Если задача ЛПi не прозондирована, переходим к шагу 2 для выполнения ветвления.
Шаг 2. (Ветвление). Выбираем одну из целочисленных переменных хj оптимальное значение хj* которой в оптимальном решении задачи ЛПi не является целым числом. Исключаем из пространства допустимых решений область [хj*] < хj < [хj*] + 1 (где [v] — наибольшее целое, не превосходящее v) путем формирования двух подзадач ЛП, которые соответствуют ограничениям хj ≤ [хj*] и хj ≥ [хj*] + 1.
Положим i = i + 1 и переходим к шагу 1.
Описанный алгоритм применим для решения задач максимизации. Для решения задач минимизации в алгоритме необходимо заменить нижнюю границу верхней (начальное значение которой равно z = +∞).
Алгоритм метода ветвей и границ непосредственно распространяется на задачи частично- целочисленного ЛП (в которых лишь некоторые из переменных должны принимать целочисленные значения). Если некоторая переменная является непрерывной, мы просто никогда не выбираем ее в качестве переменной ветвления. Допустимая подзадача определяет новую границу для значения целевой функции, если значения дискретных переменных являются целочисленными и значение целевой функции улучшено по сравнению с текущей границей.

Слайд 12Аддитивный алгоритм для задач с двоичными переменными
Любая
целочисленная переменная х, значения которой не превышают конечной верхней границы
и (т.е. 0 ≤ x ≤ и), может быть выражена через двоичные переменные с помощью представления
х = 20 у0 + 21 у1 + 22у2 + ... + 2kук,
г де k — наименьшее целое число, удовлетворяющее условию 2k + 1 – 1 ≥ u, а у0, у1, …, уk — двоичные переменные. Это представление, а также простой алгоритм (описанный ниже) решения задач ЦЛП с двоичными переменными породили надежду, что общая задача ЦЛП может быть решена более эффективно как задача с двоичными переменными. К сожалению, это направление развития методов ЦЛП не оправдало возлагаемые на него надежды.
Впервые специальный алгоритм решения задач с двоичными переменными, названный аддитивным, был предложен в 1965 году, через семь лет после создания метода ветвей и границ. Первоначально алгоритм не был связан с методом ветвей и границ, так как не требовал решения задач линейного программирования; его основные операции сводились лишь к сложению и вычитанию. Однако вскоре обнаружилась связь между этими алгоритмами. Оказалось, что аддитивный алгоритм является специальным случаем метода ветвей и границ.
Замысел эвристического зондирования в аддитивном алгоритме требует представления задачи с двоичными переменными в удобной форме, удовлетворяющей следующим требованиям.
В выражении целевой функции все коэффициенты должны быть неотрицательными, и целевая функция должна подлежать минимизации.
Все ограничения должны быть типа "≤", возможно с отрицательными правыми частями. Эти ограничения превращаются затем в равенства путем введения непрерывных дополнительных переменных в левые части ограничений.
Любая задача с двоичными переменными может удовлетворить эти условия, что демонстрирует следующий пример.

Слайд 13 Пример 6.3-2
Приведем следующую
задачу с двоичными переменными к виду, удовлетворяющему требованиям аддитивного
алгоритма.
Максимизировать z = 3х1 - 5х2
при ограничениях
x1 + х2 = 5,
4х1 + 6х2 ≥ 4,
x1, х2 = 0 или 1.
Сначала преобразуем задачу в задачу минимизации с ограничениями типа "≤".
а) Умножим z на -1, чтобы получить целевую функцию w = -3х1 + 5х2, которую следует минимизировать.
b) Преобразуем ограничение-равенство в два ограничения-неравенства типа "≤", для этого введем неравенства x1 + х2 ≤ 5 и –х1 - х2 ≤ -5.
с) Умножаем второе ограничение на -1 и получаем -4x1 - 6х2 ≤ -4.
Используя в ограничениях дополнительные переменные s1, s2 и s3, запишем задачу следующим образом.
Минимизировать w = -3х1 + 5х2
при ограничениях
x1 + х2 + s1 = 5,
–х1 - х2 + s2 = -5,
-4x1 - 6х2 + s3 = -4,
x1, х2 = 0 или 1,
s1, s2, s3 ≥ 0.
Чтобы обеспечить неотрицательность коэффициентов целевой функции, выполним подстановку хj = 1 - х'j для всех переменных хj с отрицательным коэффициентом в выражении целевой функции. В данном случае необходима подстановка х1 = 1 - х'1, после чего также надо уточнить значения правых частей ограничений. Далее аддитивный алгоритм будет иметь дело с переменными х'1 и х2.

Слайд 14 Как и в методе ветвей и границ,
ветвление в аддитивном алгоритме основывается на переменной ветвления хj. Главное
отличие в том, что здесь две ветви соответствуют строгим равенствам хj = 0 и хj = 1, так как хj является двоичной переменной. Определение границы трактуется таким же образом, как и в методе ветвей и границ, — улучшенное целочисленное решение определяет верхнюю границу минимального значения целевой функции. Зондирование подзадач может привести к одному из трех результатов.
Подзадача не может привести к допустимому решению.
Подзадача не может улучшить верхнюю границу целевой функции.
Подзадача имеет допустимое целочисленное решение.
Таким образом, возможности после решения подзадач такие же, как и в методе ветвей и границ. Основное отличие состоит в том, что здесь мы не решаем задач линейного программирования. Вместо этого используются эвристические рассуждения.
Приводимый ниже пример демонстрирует аддитивный алгоритм и его тесты зондирования подзадач.
Пример 6.3-3. (Аддитивный алгоритм)
Необходимо решить следующую задачу с двоичными переменными.
Максимизировать z = 3у1 + 2у2 - 5y3 - 2у4 + 3у5
при ограничениях
у1 + у2 + y3 + 2у4 + у5 ≤ 4,
7у1 + 3у3 - 4у4 + 3у5 ≤ 8,
11у1 - 6у2 + 3у4 - 3у5 ≥ 3,
у1, у2, y3, у4, у5 = 0 или 1.

Слайд 15 Эту задачу нетрудно представить в форме, удовлетворяющей
аддитивному алгоритму. Для этого нужно выполнить следующие действия (см. пример
9.3-2).
а) Умножаем целевую функцию на -1.
b) Умножаем третье ограничение на -1.
с) Вводим дополнительные переменные s1, s2 и s3 для преобразования ограничений в равенства.
d) Чтобы все коэффициенты целевой функции были положительны, применяем подстановки у1 = 1 – х1, у2 = 1 - х2, у5 = 1 - x5, y3 =x3 и y4 =x4.
Указанные преобразования приводят к следующей целевой функции (проверьте!). Минимизировать z' = 3x1 + 2x2 + 5x3 + 2x4 + 3x5 - 8
Для удобства будем игнорировать константу -8 и заменим z' + 8 на z, так что преобразованная задача принимает следующий вид.
Минимизировать z = 3x1 + 2x2 + 5x3 + 2x4 + 3x5
при ограничениях
- x1 - x2 + x3 + 2x4 - x5 + s1 = 1,
-7x1 + 3х3 - 4x4 - 3x5 + s2 = -2,
11x1 - 6x2 - 3x4 - 3x5 + s3 = -1,
x1, x2, x3, x4, x5 = 0 или 1.
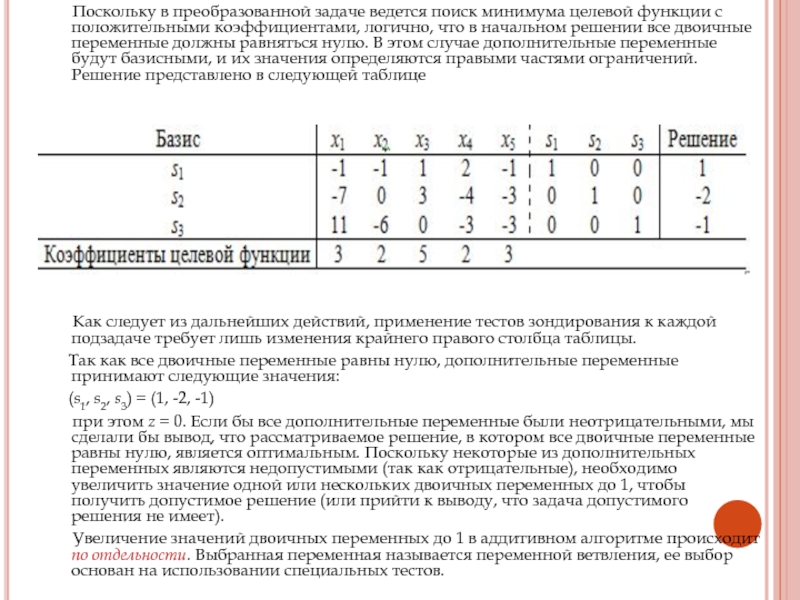
Слайд 16 Поскольку в преобразованной задаче ведется поиск минимума
целевой функции с положительными коэффициентами, логично, что в начальном решении
все двоичные переменные должны равняться нулю. В этом случае дополнительные переменные будут базисными, и их значения определяются правыми частями ограничений. Решение представлено в следующей таблице
Как следует из дальнейших действий, применение тестов зондирования к каждой подзадаче требует лишь изменения крайнего правого столбца таблицы.
Так как все двоичные переменные равны нулю, дополнительные переменные принимают следующие значения:
(s1, s2, s3) = (1, -2, -1)
при этом z = 0. Если бы все дополнительные переменные были неотрицательными, мы сделали бы вывод, что рассматриваемое решение, в котором все двоичные переменные равны нулю, является оптимальным. Поскольку некоторые из дополнительных переменных являются недопустимыми (так как отрицательные), необходимо увеличить значение одной или нескольких двоичных переменных до 1, чтобы получить допустимое решение (или прийти к выводу, что задача допустимого решения не имеет).
Увеличение значений двоичных переменных до 1 в аддитивном алгоритме происходит по отдельности. Выбранная переменная называется переменной ветвления, ее выбор основан на использовании специальных тестов.
Слайд 17 Переменная ветвления должна уменьшить (по абсолютной величине)
отрицательные значения дополнительных переменных. Как следует из приведенной таблицы, переменная
х3 не может быть выбрана в качестве переменной ветвления, так как ее коэффициенты во втором и третьем ограничениях неотрицательны. Следовательно, положив х3 = 1, мы лишь увеличим (по абсолютной величине) отрицательные значения дополнительных переменных s2 и s3. Каждая же из оставшихся двоичных переменных имеет, по крайней мере, один отрицательный коэффициент во втором и третьем ограничениях. Следовательно, комбинация этих переменных может привести к положительным значениям дополнительных переменных. Таким образом, лишь переменные x1, х2, х4 и х5 можно рассматривать в качестве возможных кандидатов на переменную ветвления.
Выбор переменной ветвления из возможных претендентов основан на использовании меры недопустимости дополнительной переменной. Эта мера, основанная на предположении, что значение двоичной переменной хj будет увеличено до 1, определяется соотношением
где si — текущее значение дополнительной переменной, аij — коэффициент при переменной хj в i-том ограничении.
В действительности Ij, есть не что иное, как сумма значений отрицательных дополнительных переменных, являющаяся результатом увеличения значения переменной хj до 1. Сложная на вид формула может быть упрощена следующим образом.

Слайд 18 Например, если мы положим х1 = 1,
то получим s1 = 1 – (-1) = 2, s2
= -2 - (-7) = 5 и s3 = -1 - 11 = -12. Следовательно, I1 = -12. Аналогично, I2 = -2, I4 = -1 и I5 = 0 (напомним, что переменная х3 была исключена из претендентов на переменную ветвления, как бесперспективная). Так как I5 имеет наименьшую меру недопустимости, переменная х5 выбирается в качестве переменной ветвления. На рис. 6.10 изображены две ветви, соответствующие х5 = 1 и х5 = 0, и образованные при этом узлы 1 и 2. Вершина 1 дает допустимое значение дополнительных переменных (s1, s2, s3) = (2, 1, 2) и z = 3. Следовательно, узел 1 прозондирован, и значение = 3 определяет текущую верхнюю границу оптимального значения целевой функции.
Рис. 6.10
Тесты, предложенные в примере 6.3-3, являются явно эвристическими, и их эффективность в исключении переменных, которые не могут инициировать процесс ветвления, зависит от того, насколько "умными" мы их конструируем. В действительности полный аддитивный алгоритм включает более сильные тесты, чем те, которые показаны в примере 6.3-3. Однако все они основаны на эвристических рассуждениях.

Слайд 19 Метод отсекающих плоскостей
Данный метод,
как и метод ветвей и границ, начинает работу с оптимального
решения "обычной" (непрерывной) задачи линейного программирования. Однако вместо ветвления и построения границ этот метод видоизменяет пространство допустимых решений, последовательно прибавляя специальным образом построенные ограничения (именуемые отсечениями). Рассмотрим сначала идею этого метода на графическом примере, а затем покажем, как отсечения строятся алгебраически.
Пример 6.3-4
Продемонстрируем применение метода отсекающих плоскостей для решения следующей задачи ЦЛП.
Максимизировать z = 7х1 + 10х2
при ограничениях
12х1 + 3х2 ≤ 6,
7х1 +x3 ≤ 35,
х1, х2 ≥ 0 и целые.
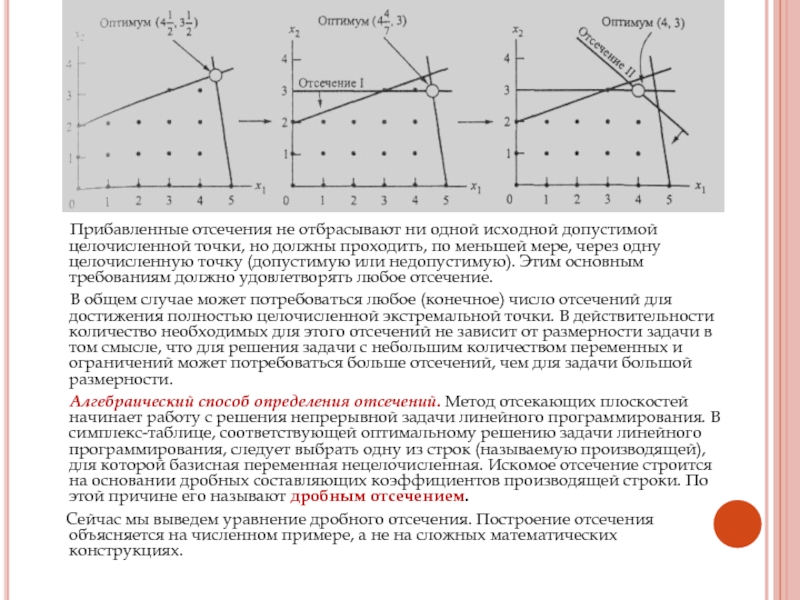
Данный метод путем добавления отсечений (отсекающих плоскостей) преобразует пространство допустимых решений соответствующей задачи линейного программирования в выпуклый многогранник, вершина которого, соответствующая оптимуму, является целочисленной и представляет решение исходной задачи. На рис. 6.13 показан пример двух таких отсечений. Мы начинаем с оптимального решения непрерывной задачи линейного программирования (х1, х2) = ( , ) и z = . Затем прибавляем отсечение I, которое вместе с ограничениями исходной задачи линейного программирования приводит к оптимальному решению (х1, х2) = (4 , с z = 62. После этого прибавляется отсечение II, которое вместе с отсечением I и исходными ограничениями приводит к оптимальному решению (х1, х2) = (4, 3) с z = 58. Последнее решение является полностью целочисленным, как и требуется.

Слайд 20 Прибавленные отсечения не отбрасывают ни одной исходной
допустимой целочисленной точки, но должны проходить, по меньшей мере, через
одну целочисленную точку (допустимую или недопустимую). Этим основным требованиям должно удовлетворять любое отсечение.
В общем случае может потребоваться любое (конечное) число отсечений для достижения полностью целочисленной экстремальной точки. В действительности количество необходимых для этого отсечений не зависит от размерности задачи в том смысле, что для решения задачи с небольшим количеством переменных и ограничений может потребоваться больше отсечений, чем для задачи большой размерности.
Алгебраический способ определения отсечений. Метод отсекающих плоскостей начинает работу с решения непрерывной задачи линейного программирования. В симплекс-таблице, соответствующей оптимальному решению задачи линейного программирования, следует выбрать одну из строк (называемую производящей), для которой базисная переменная нецелочисленная. Искомое отсечение строится на основании дробных составляющих коэффициентов производящей строки. По этой причине его называют дробным отсечением.
Сейчас мы выведем уравнение дробного отсечения. Построение отсечения объясняется на численном примере, а не на сложных математических конструкциях.
Слайд 21 Пример 6.3-5
При дополнительных переменных
х3 и х4 для ограничений 1 и 2 задачи из
примера 6.3-4 оптимальная симплекс-таблица соответствующей задачи линейного программирования имеет следующий вид.
Оптимальным непрерывным решением является х1 = , x2 = , x3 = 0, x4 = 0 и z = Целочисленное отсечение получается в предположении, что все переменные задачи являются целочисленными. Заметим также, так как коэффициенты исходной целевой функции являются целочисленными, то и значение z, соответствующее целочисленному решению, должно быть целочисленным.
Информация, содержащаяся в симплекс-таблице, соответствующей оптимальному решению, может быть записана в виде следующих уравнений.
Слайд 22 Так как в этом примере z, х1
и х2 должны быть целочисленными и все они на данный
момент имеют дробные значения в оптимальной симплекс-таблице, любое из трех уравнений можно использовать в качестве производящей строки для построения отсечения. Выберем (произвольно) дли этой цели z-уравнение.
Для построения дробного отсечения каждый из нецелочисленных коэффициентов раскладывается на целую и дробную части при условии, что дробная часть является строго положительной. Например,
Разложение коэффициентов производящей z-строки приводит к следующему уравнению.
При переносе всех целочисленных слагаемых в левую часть уравнения, а всех дробных слагаемых в правую часть получаем следующее.
Поскольку все переменные в рассматриваемой задаче принимают целочисленные значения, левая часть последнего уравнения должна быть целочисленной, откуда следует, что и правая часть также должна принимать целые значения. Перепишем ее следующим образом.
Слайд 23 Поскольку х3, х4 ≥ 0, выражение в
скобках является неотрицательным. Поэтому величина
будучи целочисленной, не может превышать 1. Следовательно, необходимое условие целочисленности можно записать следующим образом.
Это и есть отсечение, порожденное 2-строкой. Нетрудно убедиться, что ранее найденное оптимальное непрерывное решение х3 = 0, х4 = 0 не удовлетворяет отсечению. Действительно, так как х3 = х4 = 0, отсечение не удовлетворяется (оно приводит к неравенству 1 ≤ 0). Следовательно, если мы присоединим отсечение к конечной симплекс-таблице, то оптимальное решение новой симплекс-таблицы будет "двигаться" в направлении выполнения ограничения целочисленности.
Можно таким же образом построить отсечение, исходя из производящей х1 - строки или x2-строки. Рассмотрим сначала х1 - строку. Имеем
(производящая х1 - строка).
Операция разложения приводит к уравнению
Соответствующим отсечением является
(производящая х2 - строка)
записывается в виде
Следовательно, в данном случае отсечение имеет вид
Любое из трех отсечений может быть использовано на первой итерации метода отсекающих плоскостей. Поэтому нет необходимости строить все три отсечения перед выбором одного из них.
Выбирая (произвольно) отсечение, порожденное х2 - строкой, записываем его следующим образом.
(отсечение 1).
Это ограничение добавляется в качестве дополнительного в оптимальную симплекс-таблицу задачи линейного программирования.
Слайд 25 Таблица представляет оптимальное, но недопустимое решение. Для
восстановления допустимости решения применим двойственный симплекс-метод (см. раздел 4.5), что
приведет к следующей симплекс-таблице.
Из-за дробных значений переменных x1 и х3 последнее решение все еще нецелочисленное. Выберем x1 - строку в качестве производящей, т.е.
Соответствующее отсечение имеет вид
(отсечение2).
Присоединяя отсечение 2 к последней симплекс-таблице, получаем следующее.
Слайд 26 Применение двойственного симплекс-метода приводит к следующей симплекс-таблице.
Оптимальное решение (х1 = 4, x2
= 3, z = 58), определяемое последней симплекс-таблицей, является целочисленным. То, что все элементы данной симплекс-таблицы являются целочисленными, не случайность. Это типичное явление при использовании дробных отсечений.
Важно подчеркнуть, что применение дробного отсечения предполагает целочисленность всех переменных, включая дополнительные. Это значит, что данный метод применим только к решению полностью целочисленных задач.
Важность этого продемонстрируем на следующем примере. Рассмотрим ограничение
х1, х2 ≥ 0 и целые.
С точки зрения решения соответствующей задачи ЦЛП это ограничение преобразуется в уравнение путем введения неотрицательной дополнительной переменной s1, т.е.
Слайд 27 Применение дробного отсечения предполагает, что ограничение
имеет допустимое целочисленное решение по всем переменным, т.е. х1, х2
и s1. Рассмотрев это уравнение, можем сказать, что оно может иметь допустимое целочисленное решение переменных х1 и х2 лишь в том случае, если переменная s1 принимает нецелочисленные значения. Следовательно, применение дробного отсечения приведет к недопустимому целочисленному решению, так как все переменные х1, х2 и s1 не могут одновременно быть целочисленными. Тем не менее ограничение имеет допустимые целочисленные решения для рассматриваемых переменных х1 и х2.
Есть две возможности исправить эту ситуацию.
1. Можно умножить все ограничения на соответствующую константу для устранения дробей. Например, приведенное выше ограничение умножается на 6, что приводит к неравенству 6x1 + 2x2 ≤ 39. Любое целочисленное решение переменных х1 и х2 автоматически дает целочисленное значение дополнительной переменной. Однако этот тип преобразования применим лишь для простых ограничений, так как значения необходимых целочисленных коэффициентов в некоторых случаях могут быть чрезвычайно большими.
2. Можно использовать специальные отсечения, именуемые частично-целочисленными. Они ориентированы на решение задач, в которых лишь часть переменных должна принимать целочисленные значения, а остальные (включая дополнительные) остаются непрерывными. Детальное изложение таких отсечений в этой главе не рассматривается.

Слайд 288.4. ЗАКЛЮЧЕНИЕ
Наиболее важным фактором, влияющим на процесс
вычислений в целочисленном программировании, является количество целочисленных переменных. Так как
имеющиеся алгоритмы не решают задачу ЦЛП последовательно, т.е. не позволяют получать промежуточные целочисленные решения, отличные от оптимального, поэтому, с вычислительной точки зрения, в задаче ЦЛП необходимо ограничиться (по возможности) меньшим числом переменных, принимающих целочисленные значения. Следующие советы оказаться полезными при решении практических задач.
1. Аппроксимировать целочисленные переменные непрерывными, где это возможно.
2. Сузить, насколько возможно, интервалы допустимых значений целочисленных переменных.
3. Избегать в модели ЦЛП использования нелинейных элементов.
Уровень развития методов решения целочисленных задач не удовлетворяет требованиям, которые диктуются их практической важностью. Маловероятно, что в целочисленном программировании будет получен новый теоретический прорыв. Представляется более вероятным, что новые технологические достижения в области компьютерной техники могут дожить новые пути повышения эффективности алгоритмов решения задач ЦЛП.