Четность и нечетность функции

или убывание функции).
Ограниченность функции.
Наименьшее и наибольшее значение функции.
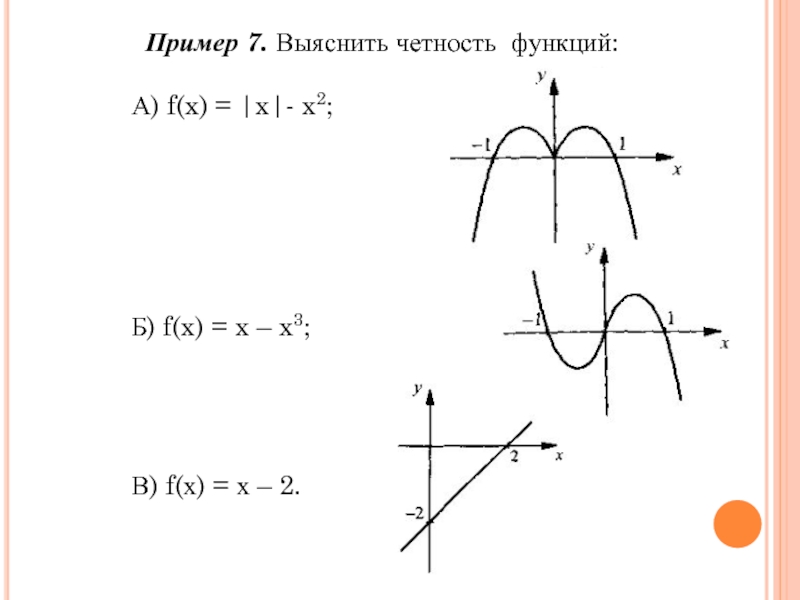
Четность и нечетность

область значений;
7) выпуклость.

8) четность.

определена и в точке х0 и в точке ( -

Пример 6. Найти область определения функции:

а)


б)

с симметричной областью определения.
Опр.8. Функция называется четной, если при изменении

Опр.9. Функция называется нечетной, если при изменении знака аргумента значение функции также меняется на противоположное,
т.е. f(– x) = – f(x).

= x – x3;




В) f(х) = х – 2.