Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числа правят миром Выполнили: ученики 10 Б класса МОУ СОШ №236
Содержание
- 1. Числа правят миром Выполнили: ученики 10 Б класса МОУ СОШ №236
- 2. Вопросы:Какова роль математикиВ жизни человека?Как числа влияют на жизнь человека?Какова история чисел?
- 3. Задачи:Понять роль математики в жизни человека;Узнать, как
- 4. Поиск информации;Создание презентации о истории возникновения счёта;Создание буклета о числах.Ход исследования
- 5. Без знания математики вся современная жизнь была
- 6. МАТЕМАТИКА И ЕЕ РОЛЬ В ЖИЗНИ ЧЕЛОВЕКА
- 7. Математика – это язык плюс рассуждения, концентрированный
- 8. Уже прошло более двухсот лет с тех
- 9. Математика, физика и астрономия – родные сестры,
- 10. Военные дела во многом зависят от математических наук .
- 11. Из истории чисел
- 12. Число — абстракция, используемая для количественной характеристики
- 13. Числа возникли из человеческих потребностей.
- 14. Первобытный человек мог сказать, что он собрал
- 15. Но шло время, и человек стал нуждаться
- 16. Считается, что термин « натурально число »
- 17. В самых древних дошедших до нас письменных
- 18. В Древнем Вавилоне дроби были шестидесятеричными и
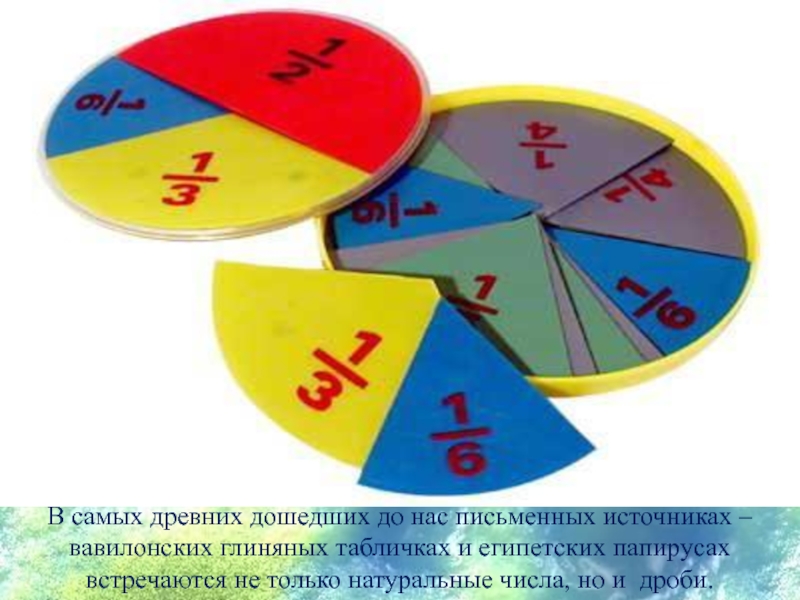
- 19. Первая дробь, с которой познакомились люди, была, наверное, половина - .
- 20. Действия над дробями еще в средние века
- 21. Понятие об отрицательных числах возникло в практике
- 22. Появилось множество рациональных чисел, которое включало в
- 23. Рациональные числа обладают свойством плотности, благодаря чему
- 24. Однако было доказано, что нельзя выразить рациональным
- 25. Рациональные и иррациональные числа объединились в новое
- 26. Символ означает отношение длины окружности к
- 27. Число, приближенно равное 2,718, которое часто встречается
- 28. Итак, типологию действительных чисел можно представить следующим образом:
- 29. Вывод.Число выступает как принцип познания и порождения,
- 30. 1. А.П.Юшкевич, История математики, Том 1, 19702.А.П.Юшкевич,
- 31. Над проектом работали:Орлов ЮрийВаккасова Марина
- 32. Руководитель.Учитель математики.ПотаповаЕлена Авиевна
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Числа правят
миром
Выполнили: ученики 10 Б класса
МОУ «СОШ №236 г.Знаменск»
Орлов
Юрий и Ваккасова Марина
Слайд 2Вопросы:
Какова роль математики
В жизни человека?
Как числа влияют на жизнь человека?
Какова
история чисел?
Слайд 3Задачи:
Понять роль математики в жизни человека;
Узнать, как появились натуральные, целые,
действительные и числа е и p;
Оформить материал в виде
презентации;Создать буклет .
Цель: познакомиться с числом и узнать как оно появилось.
Слайд 4Поиск информации;
Создание презентации о истории возникновения счёта;
Создание буклета о числах.
Ход
исследования
Слайд 5Без знания математики вся современная жизнь была бы невозможна. Например,
у нас не было бы хороших домов, потому что строители
должны уметь измерять, считать и сооружать. Наша одежда была бы очень грубой, так как ее нужно хорошо скроить, а для этого точно все измерить и др.Слайд 7Математика – это язык плюс рассуждения, концентрированный результат точного мышления
многих людей. Физик не может не знать этот язык потому,
что на этом языке написана книга природы, которую суждено ему читать.Математика и физика
Слайд 8Уже прошло более двухсот лет с тех пор, как химия
перестала быть описательной наукой. После того, как гениальный М.В. Ломоносов,
ввел в химическую практику весы, знание математики стало необходимо для каждого химика.Математика и химия
Слайд 9Математика, физика и астрономия – родные сестры, весьма почтенного возраста,
но не стареющие, а молодеющие, живущие в дружбе и союзе.
Математика и астрономия
Слайд 12Число — абстракция, используемая для количественной характеристики объектов. Возникнув ещё
в первобытном обществе из потребностей счёта, понятие числа изменялось и
обогащалось и превратилось в важнейшее математическое понятие.Слайд 14Первобытный человек мог сказать, что он собрал достаточно ягод. Охотник
с первого взгляда мог определить, что потерял одно из копий.
Слайд 15Но шло время, и человек стал нуждаться в определении количества,
то есть в числах. Пастухи должны были считать поголовье животных.
Фермерам нужно было отсчитывать сроки сезонных работ. В связи с этим и придумывались новые числа: «три», «четыре»…Слайд 16Считается, что термин « натурально число » впервые применил римский
государственный деятель, философ, автор трудов по математике и теории музыки
Боэций (480 – 524 гг.), но еще греческий математик Никомах из Геразы говорил о натуральном, то есть природном ряде чисел.Слайд 17В самых древних дошедших до нас письменных источниках – вавилонских
глиняных табличках и египетских папирусах встречаются не только натуральные числа,
но и дроби.Слайд 18В Древнем Вавилоне дроби были шестидесятеричными и записывались в виде:
, что
означало: .И сейчас, когда мы пишем ч
мин с, то по сути дела, записываем доли часа в шестидесятеричной системе счисления, т.к. мин ч, а с ч ч.
Слайд 20Действия над дробями еще в средние века считались самой сложной
областью математики. Чтобы облегчить действия с дробями и были придуманы
десятичные дроби, правила действий с которыми очень похожи на правила действий с натуральными числами.Слайд 21Понятие об отрицательных числах возникло в практике решения алгебраических уравнений,
при решении которых нередко приходилось производить вычитание большего числа из
меньшего.0
I
A
5
- 8
C
- 2
К
- 5
М
- 0,5
Р
1
0 -1 -2 -3 -4 … -
∞
1050-2035=-985
Слайд 22Появилось множество рациональных чисел, которое включало в себя целые числа
(положительные числа; числа, им противоположные, и нуль), а также дробные
числа. Эти числа удобны для вычислений.Слайд 23Рациональные числа обладают свойством плотности, благодаря чему всякий отрезок можно
с любой степенью точности измерить отрезком, принятым за единицу, и
выразить результат измерения рациональным числом. Именно поэтому рациональные числа долгое время вполне обеспечивали практические потребности людей.Слайд 24Однако было доказано, что нельзя выразить рациональным числом диагональ квадрата,
если за единицу измерения принять его сторону. Такие отрезки как
сторона квадрата и его диагональ назвали несоизмеримыми. Множества рациональных чисел недостаточно для точного измерения любых отрезков. Задача измерения несоизмеримых величин и привела к появлению иррациональных чисел. В дальнейшем древнегреческими математиками была доказана иррациональность для любого натурального , не являющегося полным квадратом.Слайд 25Рациональные и иррациональные числа объединились в новое множество – множество
действительных чисел, которое в отличии от множества рациональных чисел оказалось
непрерывным.Слайд 26Символ означает отношение длины окружности к ее диаметру. Как
число, обладает некоторыми интересными свойствами. Например, его нельзя
представить в виде отношения двух целых чисел или периодической десятичной дроби; число трансцендентно, т.е. непредставимо в виде корня алгебраического уравнения с рациональными коэффициентами.Слайд 27Число, приближенно равное 2,718, которое часто встречается в математике и
естественных науках называется «число e». Причина «вездесущности» числа e заключается
в том, что формулы математического анализа, содержащие экспоненциальные функции или логарифмы, записываются проще, если логарифмы брать по основанию e, а не 10 или какому-либо другому основанию.Слайд 29Вывод.
Число выступает как принцип познания и порождения, ибо позволяет нечто
различать, мыслить как определенное, вносить предел в мир и мысль.
Поэтому число – первое из сущего, чистое бытие, - как таковое оно есть нечто божественное: «…Природа числа, - говорит Филолай, - познавательна, предводительна и учительна для всех во всем непонятном и неизвестном. В самом деле, никому не была бы ясна ни одна из вещей – ни в их отношении к самим себе, ни в их отношении к другому, если бы не было числа и его сущности». Число есть чистое идеальное бытие, первый образ безобразного Блага и первый прообраз всего существующего. Поэтому число – наиболее достоверное и истинное, первое во всей иерархии сущего, начало космоса.Слайд 301. А.П.Юшкевич, История математики, Том 1, 1970
2.А.П.Юшкевич, История математики, Том
2, 1970
3.Г. И. Глейзер, История математики в школе, 1964
4. И.
Я. Депман, История арифметики, 1965Список литературы.