Слайд 2Математические модели и численные методы
Первый этап математического анализа – это
создание математической модели (постановка задачи). Для физического процесса модель обычно
состоит из уравнений, описывающих процесс.
Второй этап – это математическое исследование. В зависимости от сложности модели применяются различные математические методы. Часто применяются численные методы.
Третий этап – это осмысление математического решения и сопоставление его с экспериментальными данными. Проверка адекватности математической модели.
Слайд 3МЕТОДЫ ЧИСЛЕННОГО (ПРИБЛИЖЕННОГО) ИНТЕГРИРОВАНИЯ
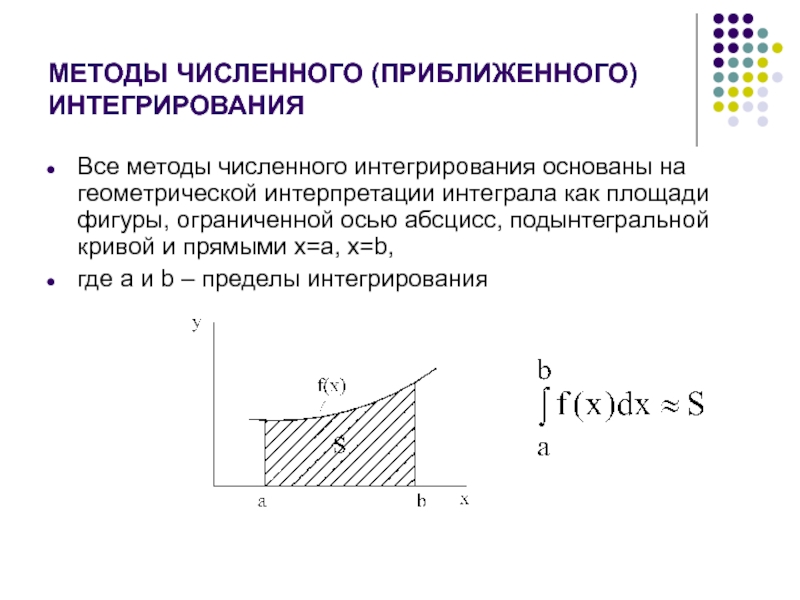
Все методы численного интегрирования основаны на геометрической
интерпретации интеграла как площади фигуры, ограниченной осью абсцисс, подынтегральной кривой
и прямыми x=a, x=b,
где a и b – пределы интегрирования
Слайд 4Формула прямоугольников
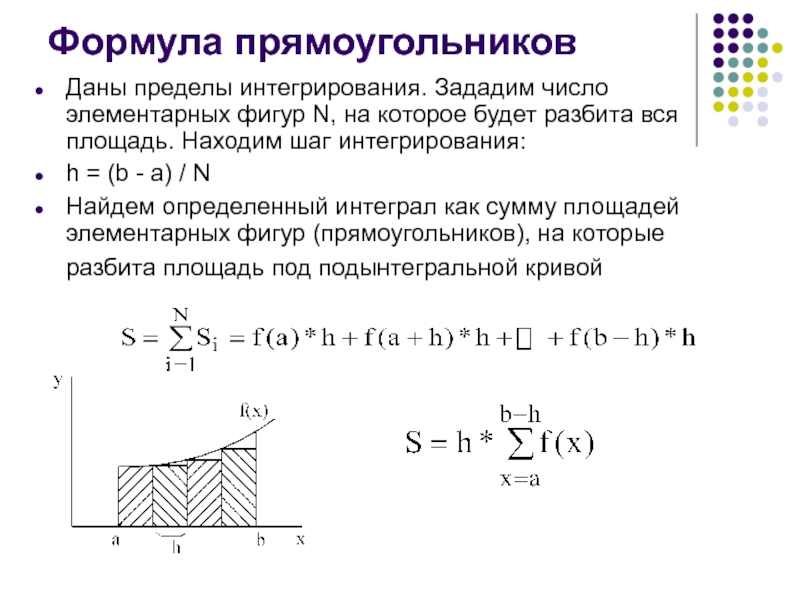
Даны пределы интегрирования. Зададим число элементарных фигур N, на
которое будет разбита вся площадь. Находим шаг интегрирования:
h = (b
- a) / N
Найдем определенный интеграл как сумму площадей элементарных фигур (прямоугольников), на которые разбита площадь под подынтегральной кривой
Слайд 5Формула трапеций
Найдем определенный интеграл как сумму площадей элементарных фигур (трапеций),
на которые разбита площадь под подынтегральной кривой
Слайд 6Формула Симпсона
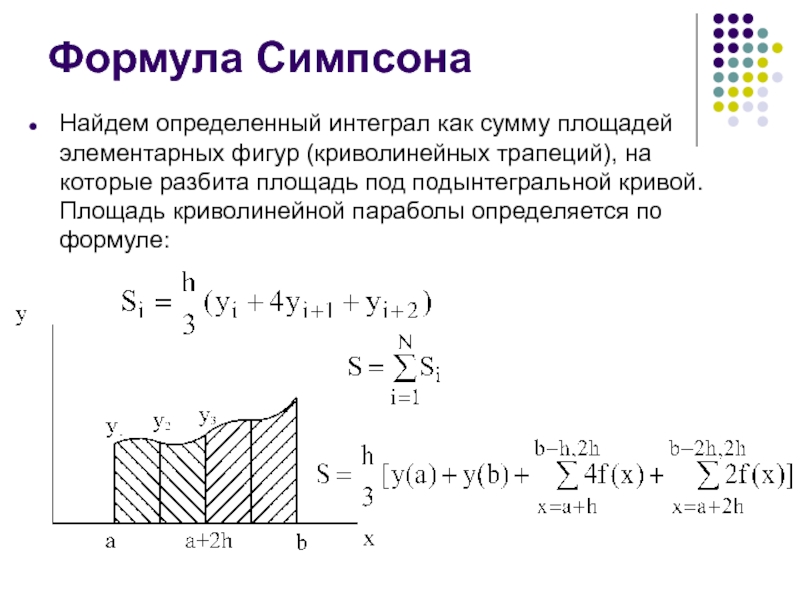
Найдем определенный интеграл как сумму площадей элементарных фигур (криволинейных
трапеций), на которые разбита площадь под подынтегральной кривой. Площадь криволинейной
параболы определяется по формуле:
Слайд 7ПРИНЦИПЫ МАШИННОГО РЕШЕНИЯ ЗАДАЧ АППРОКСИМАЦИИ И ИНТЕРПОЛЯЦИИ
Одной из важнейших
задач в процессе математического моделирования является вычисление значений функций, входящих
в математическое описание модели. Для сложных моделей подобные вычисления могут быть трудоемкими даже при использовании ЭВМ.
Поставленные проблемы решаются путем приближенной замены функции f(x) более простой функцией ϕ(x), которую нетрудно вычислять при любом значении аргумента в заданном интервале его изменения.
Приближение функции f(x) более простой функцией ϕ(x) называется аппроксимацией.
Слайд 8Аппроксимация методом наименьших квадратов (МНК)
Пусть проведено N опытов. В каждом
опыте получена пара значений xi, yi (i=1,…, N).
Необходимо провести
аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость, сглаживает возможные выбросы, возникшие за счет погрешностей эксперимента.
Слайд 9Пусть функция ϕ(x) - аппроксимирующая функция для дискретной зависимости f(xi).
В узлах xi функции f(xi) и ϕ (x) будут отличаться
на величину εi = ϕ (xi) - f(xi). Отклонения могут быть положительными и отрицательными. Чтобы не учитывать знаки, возведем отклонение в квадрат и просуммируем:
Метод построения аппроксимирующей функции из условия минимума величины Q называется методом наименьших квадратов (МНК).
Слайд 10Зададимся видом функции ϕ(x).
Обычно проводят аппроксимацию полиномами n-й степени. Общий
вид полинома n-й степени :
y = a0 + a1*x
+ a2*x2 + … + an*xn
Нахождение коэффициентов ai рассмотрим на примере аппроксимации прямой (полиномом первой степени).
y = a0 + a1*x – математическая модель
Запишем критерий МНК:
Слайд 11Ищем коэффициенты a0, a1. Исследуем функцию Q на экстремум, т.е.
найдем частные производные и приравняем нулю.
Преобразуем:
Слайд 12
Получим в итоге систему линейных уравнений:
Запишем систему в векторной форме:
D*A
= C
где A – вектор-столбец неизвестных,
С – вектор свободных членов,
D
– матрица коэффициентов.
Система линейных уравнений может быть решена либо точными методами (метод Крамера, метод обратных матриц, метод Гаусса), либо приближенными методами (метод простых итераций, метод Зейделя).
Слайд 13Интерполяция
Задача приближения таблично заданной функции многочленом, когда принимается, что заменяющая
функция должна проходить через заданные узлы, называется интерполяцией.
Частной задачей интерполяции
считают нахождение приближенных значений табличной функции при аргументах x, не совпадающих с узловыми.
В более общем плане с помощью интерполяции решают широкий круг задач численного анализа – дифференцирование и интегрирование функций, нахождение нулей и экстремумов функций, решение дифференциальных уравнений и т.д.
Возможность решения этих задач обусловлена достаточно простым видом аппроксимирующей функции ϕ(x).
Слайд 14Интерполяция полиномом Лагранжа
Пусть функция f(x) задана таблицей значений, полученной из
эксперимента или путем вычислений. Выбранные значения аргумента x называются узлами
таблицы. Считаем, что узлы не являются равноотстоящими.
Введем функцию ϕ(x) так, чтобы она совпадала с табличными значениями заданной функции f(x) во всех узлах xi:
ϕ(x, a0, a1, …,an) = fi, 0 ≤ i ≤ N (*)
Свободные параметры ai определяются из системы уравнений.
Подобный способ введения аппроксимирующей функции называется лагранжевой интерполяцией, а соотношения (*) – условиями Лагранжа.
Слайд 15Интерполяция полиномом Лагранжа
Для решения частной задачи интерполяции Лагранж предложил следующую
форму интерполяционного полинома:
Коэффициент полинома находится как отношение произведений отклонений точки
х, не принадлежащей узлу, от всех узлов (исключая i-й) и произведения отклонений i-го узла от всех остальных узлов.
X* - значение аргумента,
не совпадающее с
узловыми значениями
Слайд 16Интерполяция полиномом Ньютона
Для таблиц с равноотстоящими узлами существуют несколько видов
полиномов Ньютона
Первый полином Ньютона (для интерполяции «вперед»)
где yi – значения
дискретной функции,
Δyi, Δ2yi – конечные разности первого, второго порядка и т.д.
q определяется по формуле:
h – шаг интерполяции;
n – порядок полинома;
n=N-1
N – количество точек в таблице
Слайд 17Интерполяция полиномом Ньютона
Второй полином Ньютона (для интерполяции «назад»)
Таблица конечных разностей:
Слайд 18Численное решение обыкновенных дифференциальных уравнений (ОДУ)
ОДУ широко используется для мат.
моделирования процессов и явлений в различных областях науки и техники:
-
уравнения движения тел в механике,
- кинетика химических реакций,
- прогиб упругого стержня.
В ДУ n-го порядка в качестве неизвестных величин входят функция f(x) и ее первые n производных по аргументу x:
φ(x, y, y’, … ,y(n)) = 0 (1)
Уравнение (1) эквивалентно системе n уравнений первого порядка:
φk (x, y1, y1’, y2, y’2, … , yn, y’n ) =0, где k = 1…n (2)
Слайд 19Уравнение (1) и эквивалентная ему система (2) имеют бесконечное множество
решений.
Единственное решение выделяют с помощью дополнительных условий, которым должны удовлетворять
искомые решения.
В зависимости от вида этих условий выделяют
3 типа задач:
- задачи Коши,
- граничные задачи,
- задачи на собственные значения.
Слайд 20Задача Коши (задача с начальными условиями)
Кроме исходного уравнения (1) в
некоторой точке x0 заданы начальные условия, т.е. значения функции y(x)
и
(n-1) ее производных:
y(x0) = y0, y’(x0) = y’0, …, y(n-1)(x0) = yn-10 .
Для системы ОДУ (2):
y1(x0), y2(x0), …, yn(x0).
Слайд 21Метод Эйлера (метод ломаных)
Представим задачу (2) в каноническом виде,
в
форме Коши
y(x0)=y0
В окрестности точки x0 функцию y(x) разложим
в ряд Тейлора, который можно применить для приближенного определения искомой функции y(x):
Слайд 22В точке x0+h при малых значениях h можно ограничиться двумя
членами ряда
y(x0+h) = y0 + h*y’(x0) + O(h2),
где O(h2)
– бесконечно малая величина порядка h2.
Заменим производную y’(x0) на f(x0,y0):
y(x0+h) ≈ y0 + h* f(x0,y0) (3)
Теперь приближенное решение в точке
x1 = x0 + h можно вновь рассматривать как начальное условие и по формуле (3) найти значение функции y в следующей точке
x2 = x1+h.
Получен простейший алгоритм решения задачи Коши, который называется методом Эйлера
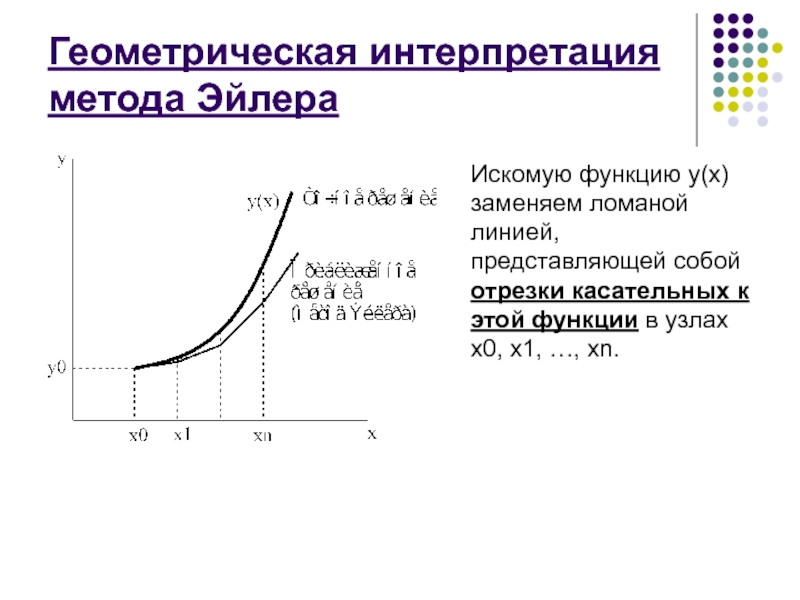
Слайд 23Геометрическая интерпретация метода Эйлера
Искомую функцию y(x) заменяем ломаной линией,
представляющей собой отрезки касательных к этой функции в узлах x0,
x1, …, xn.
Слайд 24Метод Рунге-Кутта
Для уменьшения погрешности метода интегрирования ОДУ, использующего разложение искомого
решения в ряд Тейлора, необходимо учитывать большее количество членов ряда.
Однако при этом возникает необходимость аппроксимации производных от правых частей ОДУ.
Идея методов Рунге-Кутта заключается в том, что производные аппроксимируются через значения функции f(x,y) в точках на интервале [x0, x0+h], которые выбираются из условия наибольшей близости к ряду Тейлора
Слайд 25Метод Рунге-Кутта 4го порядка
В зависимости от старшей степени h, с
которой учитываются члены ряда, существуют вычислительные схемы Рунге-Кутта разного порядка.
yi+1
= yi + Δy - рекуррентная формула Рунге-Кутта
Δy = (k1 + 2*k2 + 2*k3 + k4) / 6 - усредненное значение приращений y,
где ki – аналог Δy.
Слайд 26Метод Рунге-Кутта 4го порядка
Производная определяется в 4-х точках:
k1 = h*
y’(xi, yi)
k2 = h* y’(xi + h/2, yi + k1/2)
k3
= h* y’(xi + h/2, yi + k2/2)
k4 = h*y’(xi + h, yi + k3)
Метод Рунге-Кутта является более точным, чем метод Эйлера, т.к. чем выше порядок, тем точнее расчет приращения Δy.