Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
решение систем уравнений способом сложения
Содержание
- 1. решение систем уравнений способом сложения
- 2. Устная работа1. Выясните, является ли пара чисел (–1; 1) решением системы уравнений:данетнетда
- 3. Устная работа2. Решите систему уравнений:(-1; -2)(-2; 1)(1; 0)(1; -2)
- 4. Решим систему уравнений:1) Нельзя подобрать два таких
- 5. Решим систему уравнений:1) Очевидно, что какие бы
- 6. три возможных случая, возникающие при решении систем
- 7. С помощью графиков выясните, сколько решений имеет система уравнений:
- 8. Не выполняя построения, определите, как расположены графики уравнений системы, и сделайте вывод относительно числа ее решений:
- 9. Решите систему уравнений:
- 10. Подведём итоги– Как алгебраически найти координаты точки
- 11. Скачать презентанцию
Устная работа1. Выясните, является ли пара чисел (–1; 1) решением системы уравнений:данетнетда
Слайды и текст этой презентации
Слайд 4Решим систему уравнений:
1) Нельзя подобрать два таких числа, подстановка которых
в одинаковые выражения дает разные значения.
2) При построении получаются две
параллельные прямые, то есть система не имеет решений.3) Если найти разность левых и правых частей уравнений, то получим равенство 0 = 4, которое является неверным, что говорит о том, что система решений не имеет.
Слайд 5Решим систему уравнений:
1) Очевидно, что какие бы пары чисел, являющихся
решениями первого уравнения, мы ни нашли, они будут служить и
решениями второго уравнения, поскольку эти уравнения одинаковые.2) С геометрической точки зрения уравнения, входящие в систему, задают одну и ту же прямую (то есть прямые совпадают), поэтому система имеет бесконечно много решений.
3) Если найти разность левых и правых частей уравнений, то получим числовое равенство 0 = 0, которое является верным.
/ : 2
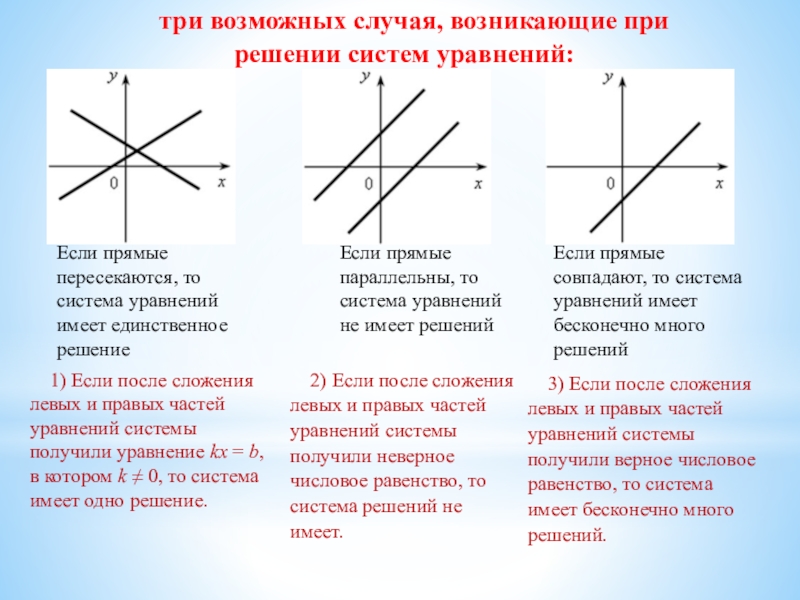
Слайд 6три возможных случая, возникающие при решении систем уравнений:
Если прямые пересекаются,
то система уравнений
имеет единственное
решение
Если прямые параллельны, то система
уравнений
не имеет решенийЕсли прямые совпадают, то система уравнений имеет бесконечно много
решений
1) Если после сложения левых и правых частей уравнений системы получили уравнение kx = b, в котором k ≠ 0, то система имеет одно решение.
2) Если после сложения левых и правых частей уравнений системы получили неверное числовое равенство, то система решений не имеет.
3) Если после сложения левых и правых частей уравнений системы получили верное числовое равенство, то система имеет бесконечно много решений.
Слайд 8Не выполняя построения, определите, как расположены графики уравнений системы, и
сделайте вывод относительно числа ее решений:
Слайд 10Подведём итоги
– Как алгебраически найти координаты точки пересечения двух прямых?
–
Что называется решением системы линейных уравнений?
– В чем заключается способ
сложения при решении систем уравнений?– Сколько решений может иметь система линейных уравнений?
– Как графически определить количество решений системы уравнений?
– Как определить с помощью способа сложения, что система уравнений не имеет решений? Имеет бесконечно много решений?
