Численные методы оптимизации_11.pptx

Он превосходит по производительности метод наискорейшего спуска и другие методы

сопряженных градиентов в различных задачах. Изначально считалось, что LMA – это комбинация простейшего градиентного метода и метода Гаусса-Ньютона, однако впоследствии выяснилось, что данный алгоритм можно также рассматривать как метод доверительных интервалов.

Метод Левенберга—Марквардта

08.11.2011

параметр на очередной итерации по правилу
2. Оценить невязку в

новом векторе параметров.
3. Если в результате вычисления параметра невязка увеличилась, вернуться на шаг назад (т.е. восстановить прежние значения весов) и увеличить в 10 раз. Затем повторить выполнение, начиная с шага 1.
4. Если в результате вычисления параметра невязка уменьшилась, принять текущий шаг (т.е. оставить новые значения весов) и уменьшить в 10 раз.

Метод Левенберга—Марквардта

08.11.2011

U и V – mxn матрицы, причем m≤n. Тогда










обратима тогда

и только тогда, когда обратима

и

Доказательство.

являются в этом случае векторами - столбцами размерности n (u

и v) и формула Шермана-Моррисона-Вудбери принимает вид

There are different versions. The first one goes directly back to Woodbury:
(1)
There is also a more general form, which can be expressed in two different ways.
The first one is easier to be understood, while the second one is more general.
(2)
The ladder results also in a special version, which I think is very nice.
(3)

REFERENCES:
Golub, G. H. and Van Loan, C. F. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins, p. 50, 1996.

определения

, где ,

Продолжая, получим и обратную матрицу
Важно отметить, что не возникает необходимости
хранить матрицы . Кроме того, для сокращения
числа операций при вычислении , определим

тогда

08.11.2011

Формула Шермана-Моррисона-Вудбери

тогда

has already been computed and it is desired to compute

(A + UCV)−1. With the inverse of A available, it is only necessary to find the inverse of C−1 + VA−1U in order to obtain the result using the right-hand side of the identity. If C has a much smaller dimension than A, this is more efficient than inverting A + UCV directly.

This is applied, e.g., in the Kalman filter and recursive least squares methods, to replace the parametric solution, requiring inversion of a state vector sized matrix, with a condition equations based solution.

In case of the Kalman filter this matrix has the dimensions of the vector of observations, i.e., as small as 1 in case only one new observation is processed at a time. This significantly speeds up the often real time calculations of the filter.

Формула Шермана-Моррисона-Вудбери

08.11.2011

на диагональ гессиана, получив
таким образом следующее правило:



Matrix inversion

plays a significant role in computer graphics, particularly in 3D graphics rendering and 3D simulations. Examples include screen-to-world ray casting, world-to-subspace-to-world object transformations, and physical simulations.

Метод Левенберга—Марквардта

08.11.2011

целевая функция
достигает минимума.
Рассмотрим задачу создания ящика прямоугольной формы,
площадь боковой

поверхности которого минимальна при
заданном объеме сосуда

Примеры задач

08.11.2011

Такая конструкция минимизирует, например, потери тепла.
Ящик открытый (без крышки).

может быть сформулирована так:
Минимизировать


при условии, что
Это задача оптимизации с

тремя искомыми параметрами и
ограничении – равенстве.
Однако задачу можно слегка упростить, заметив, что
условие ограничения объема позволяет исключить один
параметр:

Примеры задач

08.11.2011

без
ограничений:
Минимизировать


Это задача безусловной минимизации с двумя искомыми параметрами.

Оптимальное

решение исходной задачи может быть получено и в
том, и в другом случае.

Правда, надо отметить, что в исходной постановке задачи мы не
учли тот факт, что отрицательные искомые параметры не имеют
практического смысла.

Примеры задач

08.11.2011

приводит к введению
ограничений – неравенств.
Минимизировать



или
Примеры задач
08.11.2011

пойти
на некоторое упрощение исходных условий. Предположим, что
можно ограничиться рассмотрением ящиков

с квадратным дном,
то есть добавить условие .
Объем и площадь поверхности вычисляются по формулам


Задача минимизации (функции одной переменной) теперь
выглядит так:
Минимизировать

Примеры задач

08.11.2011

объеме .

Минимум достигается при

08.11.2011

Примеры задач

LLC 2008
Alfio Quarteroni, Riccardo Sacco, Fausto Saleri. Numerical mathematics. 2000,

Springer-Verlag New York, Inc.

Литература

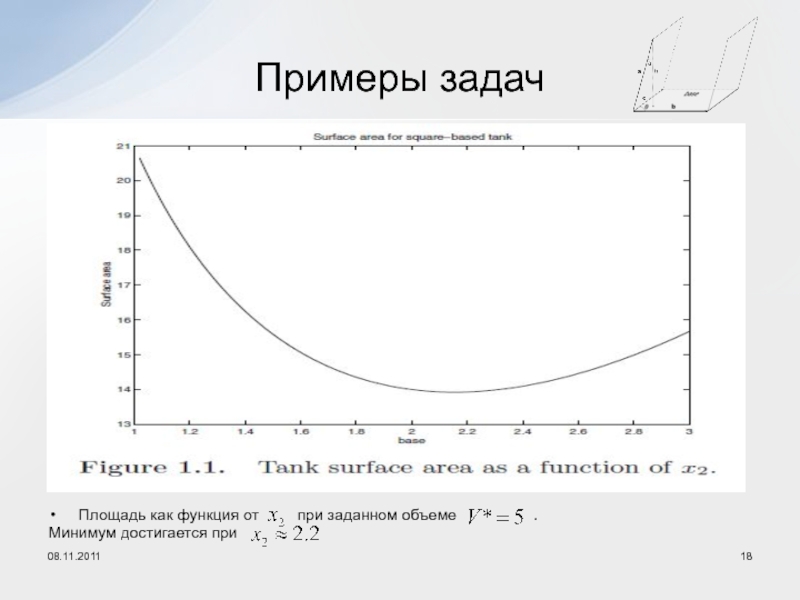
08.11.2011