Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Циклический код
Содержание
- 1. Циклический код
- 2. Циклический код представляет собой разновидность группового кода
- 3. Циклические коды незаменимы при передаче информации в
- 4. Среди групповых кодов можно выбрать такие, у
- 5. Сдвиг осуществляется справа налево, а крайний левый
- 6. Любые «k» строк этой матрицы линейно независимы
- 7. В циклическом коде кодовые комбинации удобно записывать
- 8. Например:Посмотрим, что происходит при циклическом сдвиге:Предыдущие строки,
- 9. Посмотрим, делится ли полученный многочлен на
- 10. Образующий многочлен g(x).Многочлен, с помощью которого образуются
- 11. Для обнаружения ошибок в циклических кодах принятую
- 12. Широко применяется потому чтооперации умножения и деления
- 13. Циклический кодМатематическое введение
- 14. Разрешенную кодовую комбинацию Ц.К. можно рассматривать как
- 15. Обе коммутативныассоциативны, то есть;и связаны законом дистрибутивности:
- 16. Правила выполнения операцийНужно чтобы замкнутое множество многочленов (n – 1) степени образовало кольцо
- 17. Правило 1. СложениеВ качестве операции сложения выберем сложение по модулю два без переноса в старший разряд
- 18. Правило 2. УмножениеОперация умножения по обычным правилам
- 19. Пример: Сдвиг с переносом единицы из старшего
- 20. Поделим на многочлен Получим в остатке
- 21. ИДЕАЛПри выбранных операциях и все множество многочленов
- 22. Количество элементов в идеале зависит от вида
- 23. Циклический кодТребования к образующему многочлену
- 24. Разрешенная кодовая комбинация Ц.К. должна делиться на
- 25. поэтому i-тую строку матрицы ƒi(x) можно записать:где
- 26. делится на g(x) без остатка. Поэтому, чтобы
- 27. Если мы выбрали g(x) так, что он
- 28. Наибольшее число остатков дает неприводимый многочлен степени
- 29. Выбор образующего многочлена циклического кода по требуемой корректирующей способностиВыбор образующего многочлена для обнаружения одиночных ошибок
- 30. Принятую искаженную кодовую комбинацию можно представить как:где
- 31. Выбираем многочлен g(x), чтобы при делении на
- 32. Выбираем многочлен g(x), чтобы при делении на
- 33. Например, для кода (7; 4) ошибка в
- 34. Обратим внимание, что для обнаружения одиночной ошибки
- 35. во многих случаях целесообразнопользоваться таблицей наилучших двоичных циклических кодов, предлагаемой ITU (International Telecommunication Union)
- 36. Из соотношения (2n–k – 1) ≥ числа
- 37. .К.К. будет делится на без остатка, если в
- 38. Где ее записывать, вначале К.К. или в конце значения не имеетПоделим РКК на
- 39. Замечаниециклический код с проверкой на четность обнаруживает
- 40. Неприводимые многочлены
- 41. Еще таблица
- 42. Выбор образующего многочлена циклического кода по требуемой корректирующей способностиВыбор образующего многочлена для исправления одиночных ошибок
- 43. Для исправления одиночных ошибок в n разрядной
- 44. Из последнего равенства определяется число проверочных разрядов
- 45. Для исправления одиночных ошибок минимальная дистанция между
- 46. Например: Пусть n = 15; S =
- 47. Нас интересуютнеприводимые многочлены степени m = 4.
- 48. Векторы ошибок младших разрядов имеют вид:
- 49. Степени соответствующих им многочленов меньше степени образующего
- 50. Однако использовать для тех же целей многочлен
- 51. Из приведенного примера следует, что в качестве
- 52. Выбор образующего многочлена циклического кода по требуемой корректирующей способностиНахождение образующего многочлена, обнаруживающего двойные ошибки
- 53. Вектор двойных ошибок можно записать:где λ = i – j > 0, а i > j.
- 54. Для того, чтобы обнаруживать двойные ошибки, необходимо,
- 55. Для обнаружения двойных ошибок (R = 2),
- 56. Таким образом, образующий многочлен, исправляющий одиночные ошибки,
- 57. Выбор образующего многочлена циклического кода по требуемой корректирующей способностиОбнаружение ошибок произвольной кратности
- 58. Если известен образующий многочлен g(x) степени m,
- 59. Например:n = 15; k = 11; m
- 60. Это эквивалентно добавлению еще одного проверочного разряда,
- 61. Но возможно и другое решение: n оставляется
- 62. Чтобы построить код, обнаруживающий ошибки произвольной кратности
- 63. Методы построения циклического кода
- 64. Зная кодовую комбинацию из «k» информационных символов
- 65. Методы построения циклического кода методом умножения
- 66. Информационный многочлен ai(x) умножается на образующий многочлен
- 67. ПримерПусть имеем код (7; 4), то есть
- 68. Для получения Р.К.К. –умножим и получим ƒi(x)
- 69. В линии связи произошла ошибка , на выходе из л.с. получим кодовую комбинацию:
- 70. На приемной стороне, чтобы судить есть ошибка
- 71. Получили остаток, отличный от нуля. По нему
- 72. До ошибки в четвертом разряде остаток соответствует
- 73. В примере остаток , то есть ошибка в пятом разряде. Исправим ошибку:
- 74. Но, получив ƒi(x), мы не получили ai(x), то есть снова приходится делить ƒi(x) на g(x):
- 75. Методы построения циклического кодаметодом деления
- 76. Чтобы получить разделимый код : ai(x) умножают
- 77. Разрешенная кодовая комбинация ƒi(x) получается путем сложения и r(x)
- 78. Степень многочлена g(x) – m, а
- 79. Пример (тот же)ai(x) = 1011; g(x) = 1011.Так получилось потому, что ai(x) совпало с g(x).
- 80. Если в линии связи произошла ошибка в
- 81. Исправим принятую К.К.:И сразу получаем ai(x) как первые k символов, то есть 1011.
- 82. Методы построения циклического кодаПо методу группового кода
- 83. Ц.К. является разновидностью группового кода (Г.К.), а
- 84. Зная значения информационных разрядов a0 (старший разряд);
- 85. Реализация кодирующих устройств циклического кодаметодом умножения
- 86. Нарисуем схему умножения образующего многочлена g(x) на
- 87. Входной сигнал подается в ячейки памяти слева,
- 88. В нашем случае это x3; x1 и x0,
- 89. В результате получается на выходе тот же результат, что и при умножении столбиком
- 90. Скачать презентанцию
Циклический код представляет собой разновидность группового кода и не отличается от него по уровню помехозащищенности, но благодаря простоте технической реализации нашел широкое применение.
Слайды и текст этой презентации
Слайд 3Циклические коды
незаменимы при передаче информации в каналах связи, в
которых отсутствует возможность повторной передачи данных
Циклические коды применяются:
при записи и
считывании на HDD, CD и DVD, при использовании USB-портов для обмена информацией,
при передаче аудио и видео информации.
Слайд 4Среди групповых кодов можно выбрать такие, у которых строки связаны
условием цикличности,
т.е. все строки матрицы могут быть получены циклическим
сдвигом одной строки, которая называется образующей или производящей. Слайд 5Сдвиг осуществляется справа налево, а крайний левый символ перемещается в
конец строки, т.е. в крайнее правое положение.
Например:
Коды, у которых строки
матрицы удовлетворяют этому условию, называются циклическимиСлайд 6Любые «k» строк этой матрицы линейно независимы и могут служить
основой для получения любой разрешенной кодовой комбинации циклического кода.
Число возможных
циклических кодов существенно меньше числа групповых кодов.Слайд 7В циклическом коде кодовые комбинации удобно записывать в виде многочлена
(n – 1) степени относительно фиктивной переменной x.
Показатель степени
при x соответствует номеру разряда, уменьшенному на единицу. Младший разряд соответствует x0 = 1. Коэффициенты при x имеют значения 0 или 1.
Слайд 8Например:
Посмотрим, что происходит при циклическом сдвиге:
Предыдущие строки, кроме последней, давали
кодовую комбинацию путем умножения сомножителя на x в степени, соответствующей
количеству сдвигов влево с переносом на освобождающееся знакоместо нуля.Последняя кодовая комбинация получена путем переноса на крайнее правое место единицы.
Слайд 10Образующий многочлен g(x).
Многочлен, с помощью которого образуются все разрешенные кодовые
комбинации, называется образующим и в дальнейшем будем обозначать его g(x).
Слайд 11Для обнаружения ошибок
в циклических кодах принятую кодовую комбинацию делят
на образующий многочлен.
Если остаток от деления R(x) = 0,
то принимается решение, что ошибок нет. Если R(x) ≠ 0, то были ошибки. Вектор ошибок определяется по виду остатка.
Слайд 12Широко применяется потому что
операции умножения и деления многочленов просто реализуются
на регистрах сдвига с обратными связями.
Слайд 14Разрешенную кодовую комбинацию Ц.К. можно рассматривать как
элемент подмножества множества
многочленов степени не выше (n – 1).
Для анализа Ц.К.
используется аппарат теории колец.Коммутативным кольцом называется множество, в котором определены две операции: сложение и умножение.
Обе коммутативны
Слайд 16 Правила выполнения операций
Нужно чтобы замкнутое множество многочленов (n –
1) степени образовало кольцо
Слайд 17Правило 1. Сложение
В качестве операции сложения выберем сложение по модулю
два без переноса в старший разряд
Слайд 18Правило 2. Умножение
Операция умножения по обычным правилам не проходит, так
как нарушается условие замкнутости:
Введем операцию символического умножения по следующим правилам:
Умножение
выполняется по обычным правилам с приведением подобных членов путем сложения по модулю два;если полученный многочлен имеет степень меньше чем (n – 1), то он и принимается за результат умножения, если же степень больше чем (n – 1), то он делится на двучлен c записью в качестве результата умножения остатка от деления.
Слайд 19Пример: Сдвиг с переносом единицы из старшего разряда в младший
Имеем:
После
сдвига, соответствующего умножению на x, получим:
, что недопустимо, так
как x7 имеет степень более разрешенной xn–1, в данном случае соответствует x6.Поделим на многочлен
Поделим на многочлен
Слайд 20Поделим на многочлен
Получим в остатке R(x):
В качестве результата умножения
принимаем R(x), что соответствует переносу единицы из старшего разряда в
младший.Слайд 21ИДЕАЛ
При выбранных операциях и все множество многочленов степенью ≤ (n
– 1) образуют кольцо.
Подмножество многочленов в кольце, кратных образующему
многочлену g(x), называется идеалом, порождаемым g(x).Слайд 22Количество элементов в идеале зависит от вида g(x)
Если g(x) =
0, то в идеале всего один элемент «0».
Если g(x)
= 1, то в идеал входят все элементы кольца. Если g(x) многочлен степени m = n – k, то число элементов в идеале – 2k. Эти элементы и есть искомый нами Ц.К.
Построение Ц.К. сводится к выбору образующего многочлена g(x) с заданными корректирующими способностями
Слайд 24Разрешенная кодовая комбинация Ц.К. должна делиться на g(x) без остатка
Для
этого необходимо, чтобы на g(x) делились все многочлены образующей матрицы
кода.Каждая строка матрицы получается циклическим сдвигом образующего многочлена g(x) с приведением по модулю
Слайд 25поэтому i-тую строку матрицы ƒi(x) можно записать:
где c = 1,
если максимальная степень многочлена больше (n – 1);
c = 0,
если имеет степень < n.Слайд 26делится на g(x) без остатка.
Поэтому, чтобы ƒi(x) делилось на
g(x) без остатка, необходимо, чтобы делилось на g(x) тоже без
остатка.Слайд 27Если мы выбрали g(x) так, что он является делителем двучлена
то :
любой элемент кольца
либо делится на g(x)
без остатка и тогда входит в идеал, либо образует некоторый остаток – ri(x), который и является опознавателем ошибки.
Чем больше остатков, тем больше ошибок может исправлять выбранный образующий многочлен g(x).
Слайд 28Наибольшее число остатков дает неприводимый многочлен степени «m», когда m;
n и k связаны между собой условиями:
m = n
– k, а
n = 2m – 1.
Слайд 29Выбор образующего многочлена циклического кода по требуемой корректирующей способности
Выбор образующего
многочлена для
обнаружения одиночных ошибок
Слайд 30Принятую искаженную кодовую комбинацию можно представить как:
где ЗККi+j – запрещенная
(искаженная) кодовая комбинация;
ƒi(x) – i-тая разрешенная кодовая комбинация;
– вектор ошибки в j-том разряде, то есть X j.Ошибка обнаруживается, если при делении ЗККi+j на g(x) образуется остаток.
Но ƒi(x) делится на g(x) без остатка.
Поэтому нужно выбрать такой многочлен g(x), чтобы при делении на g(x) получился остаток.
Слайд 31Выбираем многочлен g(x), чтобы при делении на g(x) получился остаток
Из
всех многочленов g(x), удовлетворяющих этому условию необходимо взять тот, который
имеет минимальную степень, так как это обеспечивает минимум проверочных разрядов.Кроме того,
g(x) должен входить в разложение многочлена .
Слайд 32Выбираем многочлен g(x), чтобы при делении на g(x) получился остаток
Таким
многочленом является многочлен , который при делении всех элементов кольца
на него дает два случая:R(x) = 0, то есть элемент кода принадлежит идеалу;
R(x) = 1, то есть элемент кода имеет ошибку.
Вектор ошибки X j имеет единицу в одном из разрядов.
Слайд 33Например, для кода (7; 4)
ошибка в четвертом разряде имеет
вид 0001000.
При делении X j на всегда получаем остаток
R(x) = 1.Слайд 34Обратим внимание,
что для обнаружения одиночной ошибки дистанция между двумя
Р.К.К. должна быть не менее, чем в 2 символа, так
как d ≥ r + 1 = 1 + 1 = 2 и в принятом нами тоже 2 символа.g(x) выбираем из таблицы многочленов, не приводимых над полем по условию d = 2. Таких многочленов всего один
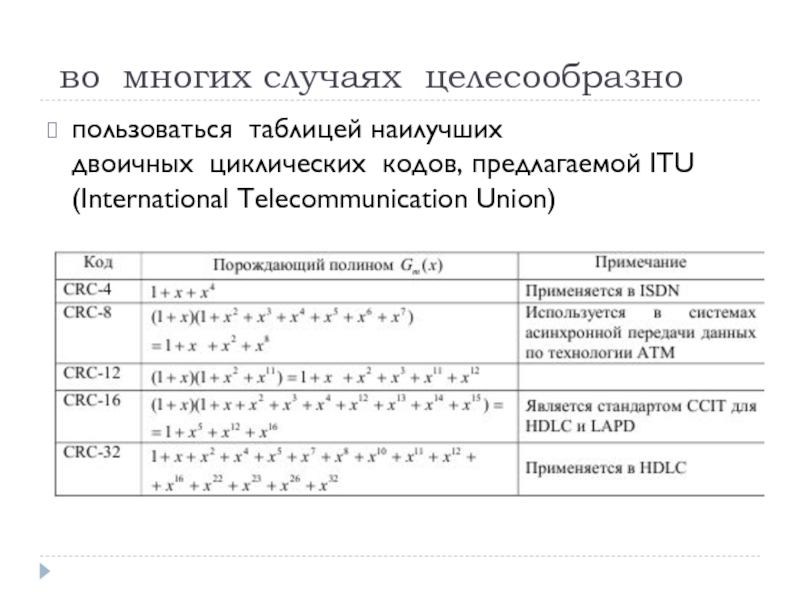
Слайд 35 во многих случаях целесообразно
пользоваться таблицей наилучших
двоичных циклических кодов, предлагаемой
ITU (International Telecommunication Union)
Слайд 36Из соотношения (2n–k – 1) ≥ числа ошибок, которые мы
хотим обнаруживать.
Так как мы обнаруживаем лишь факт есть ошибка
(в любом разряде) или ее нет, то неравенство можно записать так:2n–k – 1 ≥ 1, то есть, 2n–k ≥ 2, то есть n – k = 1; n = k + 1.
Это соответствует одному дополнительному разряду, который следует заполнить нулем или единицей, так, чтобы полученная Р.К.К. делилась без остатка
Слайд 37.К.К. будет делится на без остатка, если в ней будет четное
число единиц. Убедимся в этом.
Пусть k = 7. Имеем К.К.
Дополним ее поверочным разрядом: так как в информационных разрядах всего 3 единицы, то в поверочном разряде должна быть записана единица, чтобы полученная Р.К.К. делилась без остатка.
Слайд 39Замечание
циклический код с проверкой на четность обнаруживает не только единичные,
но и любые ошибки нечетной кратности,
так же как не
обнаруживает любые ошибки четной кратности. Слайд 42Выбор образующего многочлена циклического кода по требуемой корректирующей способности
Выбор образующего
многочлена для исправления одиночных ошибок
Слайд 43Для исправления одиночных ошибок в n разрядной К.К. необходимо определить,
какой разряд был искажен. Поэтому каждому вектору ошибки необходимо сопоставить
свой остаток.Для исправления одиночной ошибки должно быть выполнено условие:
2n – k – 1 = 2m – 1 ≥ Cn1 = n,
то есть 2m ≥ n + 1;
Слайд 44Из последнего равенства определяется число проверочных разрядов – это целое
число с округлением log2(n + 1) в большую сторону.
В
теории кодирования доказано, что если m и n связаны условием n = 2m – 1, то многочлен может быть представлен произведением всех без исключения неприводимых многочленов степени которых являются делителями числа «m» от единицы до «m». Причем всегда имеется хотя бы один многочлен степени «m».
Слайд 45Для исправления одиночных ошибок минимальная дистанция между двумя Р.К.К. должна
быть:
d ≥ 2S + 1 = 2·1 + 1 =
3.Таким образом, нам потребуется выбрать g(x), удовлетворяющий двум условиям:
и d = 3, где m – максимальная степень образующего многочлена,
а d – количество значащих членов в нем.
Слайд 46Например:
Пусть n = 15; S = 1; тогда 2n –
k – 1 ≥ n, откуда k = 11 и
m = n – k = 15 – 11 = 4 илиДелителями числа «m» являются: 1; 2; 4. Разложим на сомножители:
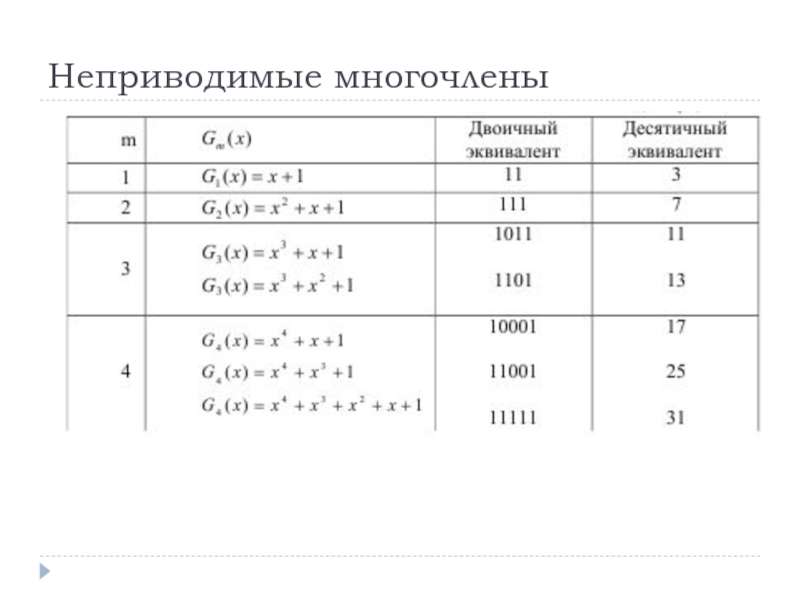
Слайд 47Нас интересуют
неприводимые многочлены степени m = 4.
Таких многочленов в
разложении – три.
Проверим, дают ли они n = 15
различных остатков, чтобы поставить им в соответствие ошибки в различных разрядах. Пусть g(x) = х4 + х3 + 1
Остатки будем получать путем деления X j на g(x).
Слайд 49Степени соответствующих им многочленов меньше степени образующего многочлена g(x). Поэтому
они сами являются остатками при нулевой целой части.
Остаток, соответствующий
вектору ошибки в следующем старшем разряде, получаем при делении 00...10000 на 11001, т.е.Получили 15 различных остатков, а шестнадцатый остаток такой же, как первый.
Слайд 50Однако использовать для тех же целей многочлен
x4 + х3
+ х2 + x + 1 нельзя.
При проверке числа
различных остатков обнаруживается, что их у него не 15, а только 5Это объясняется тем, что многочлен x4 + х3 + х2 + x + 1 входит в разложение не только двучлена x15 + 1, но и двучлена х5 + 1.
Слайд 51
Из приведенного примера следует, что в качестве образующего следует выбирать
такой неприводимый многочлен g(x), который, являясь делителем двучлена хn+1, не
входит в разложение ни одного двучлена типа x^ λ+1, степень которого λ меньше nВ этом случае говорят, что многочлен q(x) принадлежит показателю степени n.
Слайд 52Выбор образующего многочлена циклического кода по требуемой корректирующей способности
Нахождение образующего
многочлена, обнаруживающего двойные ошибки
Слайд 54Для того, чтобы обнаруживать двойные ошибки, необходимо, чтобы при делении
ei+j(x) на g(x) мы имели остаток.
Но это условие всегда выполняется,
если в качестве g(x) взять многочлен, предназначенный для исправления одиночных ошибок, так как он не кратен X j и не входит в разложение (xλ 1), если λ < n.Слайд 55Для обнаружения двойных ошибок (R = 2), необходимо,
чтобы минимальная
дистанция между Р.К.К. была
d ≥ R + 1 =
2 + 1 = 3, что соответствует исправлению одиночной ошибки
d ≥ 2S + 1 = 2 · 1 + 1 = 3.
Слайд 56Таким образом, образующий многочлен, исправляющий одиночные ошибки, может обнаруживать и
двойные ошибки. Но только или то или другое, но не
одновременно и то, и другое.Слайд 57Выбор образующего многочлена циклического кода по требуемой корректирующей способности
Обнаружение ошибок
произвольной кратности
Слайд 58Если известен образующий многочлен g(x) степени m, обнаруживающий ошибки кратности
до R включительно в n-разрядном коде,
то образующий многочлен, обнаруживающий
ошибки кратности до (R + 1) получается следующим образом:Слайд 59Например:
n = 15;
k = 11;
m = 4;
g(x) =
x4 +x3 +1 – исправляет одиночные ошибки.
Значит, он может обнаруживать
и двойные ошибки. Нужно построить код, который может обнаруживать тройные ошибки.
Слайд 60
Это эквивалентно добавлению еще одного проверочного разряда,
то есть при
k = 11;
m = 4 + 1 = 5
и n = k + m = 16.
Слайд 61Но возможно и другое решение:
n оставляется равным 15,
а
так как m = 5, то k получается равным 10
Слайд 62Чтобы построить код, обнаруживающий ошибки произвольной кратности R следует :
Найти
многочлен g(x), обнаруживающий ошибки кратности (R – 1).
Помножить этот многочлен
на (x 1), что эквивалентно добавлению еще одного проверочного разряда, и получить новый g1(x). При фиксированном k, увеличивается число проверочных разрядов m; а при фиксированном n – уменьшается число информационных разрядов кода.
Необходимо убедиться, что полученный код способен исправлять ошибки во всех разрядах кодовой комбинации.
Слайд 64Зная кодовую комбинацию из «k» информационных символов – ai(x) и
образующий многочлен – g(x), нужно получить разрешенные кодовые комбинации (Р.К.К.)
– ƒi(x).Существуют три метода образования Р.К.К. циклического кода:
Методом умножения
Методом деления
Методом группового кода
Слайд 66Информационный многочлен ai(x) умножается на образующий многочлен g(x)
Достоинство метода –
простота реализации при кодировании.
Недостаток – получаемый код – неразделимый, не
ясно где расположены информационные и проверочные символы. Поэтому при декодировании после исправления ошибок приходится делить на g(x) дважды, чтобы получить информационный многочлен.
Слайд 67Пример
Пусть имеем код (7; 4),
то есть код исправляющий одиночные
ошибки.
Пусть g(x) = x3 x 1.
Необходимо передать ai(x)
= 1011.Слайд 70На приемной стороне, чтобы судить есть ошибка или нет, необходимо
принятую кодовую комбинацию (К.К.) поделить на g(x).
Если ошибок нет,
то остаток от деления r(x) должен быть равен нулю. Делим:Слайд 71Получили остаток, отличный от нуля.
По нему мы должны определить,
в каком разряде имеет место ошибка.
Для этого необходимо определить,
какой остаток ri(x) даст единичная ошибка в i-том разряде.Слайд 72До ошибки в четвертом разряде остаток соответствует самой ошибке, а
начиная с ошибки в 4-ом разряде происходит деление.
Слайд 76Чтобы получить разделимый код :
ai(x) умножают на xm
что
эквивалентно
дописыванию к ai(x) справа m нулей.
Полученный многочлен делится
на g(x). В результате получается частное от
деления g(x) и остаток r(x).
Слайд 78Степень многочлена g(x) – m, а степень остатка – (m
– 1).
Поэтому сложение эквивалентно приписыванию остатка r(x) к ai(x),
так как m разрядов в – нулевые.В то же время ƒi(x) делится на g(x) без остатка так как:
Данная методика используется при k > m.
Слайд 80Если в линии связи произошла ошибка в пятом разряде ,
то будем иметь
Поделим на g(x) и получим остаток r(x)
Слайд 83Ц.К. является разновидностью группового кода (Г.К.),
а в Г.К. проверочные
символы определяются как комбинация информационных.
Для определения проверочных символов воспользуемся
рекуррентным соотношением:Слайд 84Зная значения информационных разрядов a0 (старший разряд); a1; a2;... ak–1
можно получить значения проверочных разрядов ak; ak+1;... an–1
Получается код, полностью
совпадающий с кодом, полученным делением.Метод применяется при m > k и k = n – m, если n = 2m – 1.
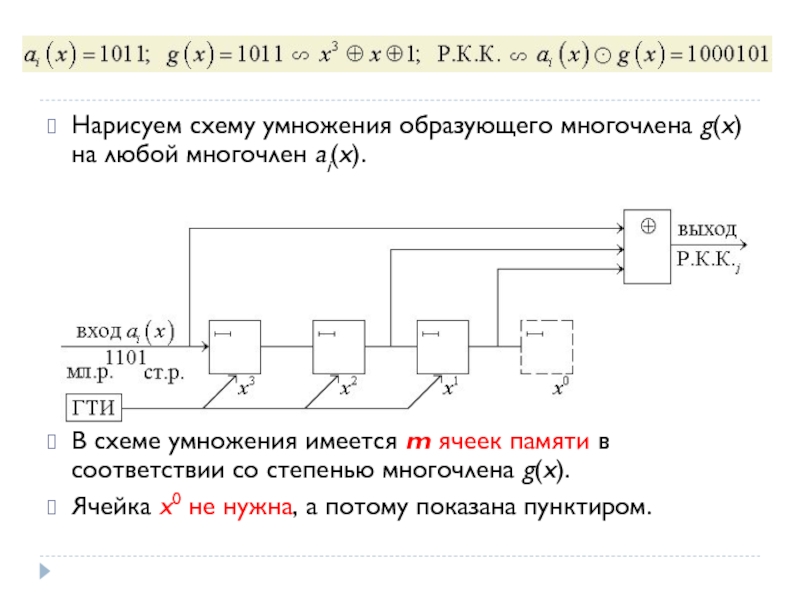
Слайд 86Нарисуем схему умножения образующего многочлена g(x) на любой многочлен ai(x).
В
схеме умножения имеется m ячеек памяти в соответствии со степенью
многочлена g(x).Ячейка x0 не нужна, а потому показана пунктиром.
Слайд 87
Входной сигнал подается в ячейки памяти слева, начиная со старших
разрядов.
Входной сигнал по тактам продвигается по ячейкам памяти в
соответствии с частотой генератора тактовых импульсов (ГТИ).За один такт продвигается вправо содержание всех ячеек памяти одновременно.
На выходной сумматор по модулю два поступают синхронно те нули и единицы, которые идут в соответствующие ячейки памяти.
Слайд 88В нашем случае это x3; x1 и x0,
то есть ячейки,
соответствующие наличию единицы в записи g(x) = 1011 = x3
x 1.Сигнал, поступающий в ячейку x2, на сумматор не идет.




































































































![БМ [Восстановленный] - копия](/img/thumbs/1fbbafc5dd4e436e6a7edb8068bf50b3-800x.jpg)



