Деформация

связывают с изменением формы и размеров тела.
Если устранение

причины деформации (разгрузка) приводит к исчезновению деформации, то деформацию называют упругой или обратимой.
Если устранение причины деформации не приводит к полному исчезновению деформации, то оставшуюся часть деформации называют необратимой или пластической.
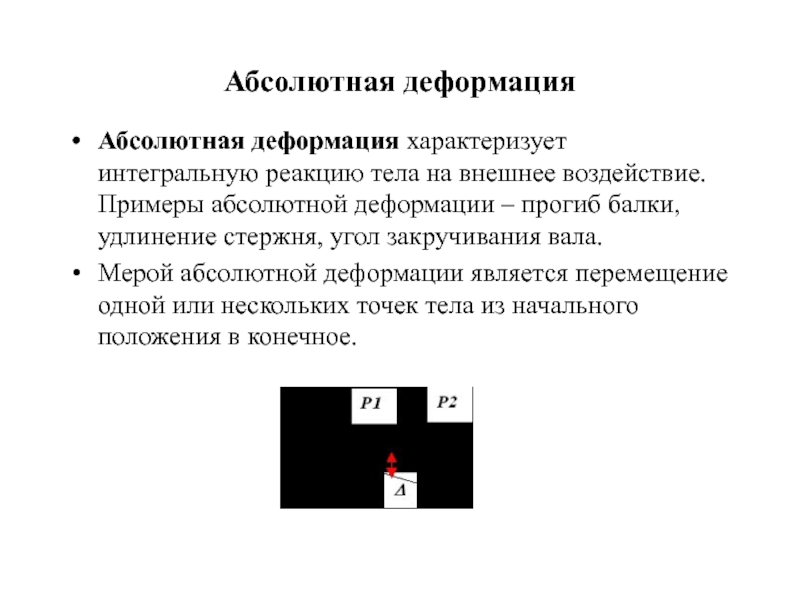
Различают абсолютную деформацию и относительную деформацию

воздействие. Примеры абсолютной деформации – прогиб балки, удлинение стержня, угол

закручивания вала.
Мерой абсолютной деформации является перемещение одной или нескольких точек тела из начального положения в конечное.

вводят понятие относительной деформации.
Относительная деформация характеризует реакцию рассматриваемой точки (области)

тела на внешнее воздействие.
Различают линейную и угловую относительную деформацию
Под точкой тела в сопротивлении материалов понимают объем некоторого элементарного параллелепипед.

параллелепипед стал косоугольным.

действием сил, направление действия которых совпадает с осью стержня, проходящей

по центрам тяжести всех нормальных сечений стержня.

деформаций и перемещений сечений.
Дан стержень,

закрепленный с одного конца

действующих по одну сторону от сечения. Сила, направленная справа налево,

берется со знаком «плюс» .