TheSlide.ru

Дискретная математика

Содержание

1. Дискретная математика
2. Тупиковая ДНФОтношение покрытия между единичными наборами и импликантами ДНФ наглядно задается таблицей покрытия.
3. Таблица покрытияСтроки таблицы соответствуют конъюнкциям ДНФ, столбцы
4. ПримерПусть ДНФ функции имеет вид:Тогда ее единичное множество может быть представлено в виде:Построим таблицу покрытия.
5. Пример:Из таблицы видно, что вторая строчка –
6. Значит, импликант yz – лишний импликант.ПримерТаким образом,
7. Тупиковая ДНФ Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой.
8. Замечание 1Чтобы с помощью таблицы покрытия получить
9. Замечание 2У функции может быть несколько тупиковых
10. Метод Блейка-Порецкого –метод получения сокращенной ДНФ, содержащей
11. Метод Блейка-Порецкого3. Допишем к списку полученных конъюнкций
12. Пример 1Дана СДНФ вида:Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.
13. Метод Блейка-ПорецкогоП. 1.
14. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-ПорецкогоПостроим таблицу покрытия:
15. Таблица покрытия
16. Таблица покрытия
17. Таблица покрытия
18. Таблица покрытия
19. Пример 2Дана СДНФ вида:Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.
20. Метод Блейка-ПорецкогоП. 1.
21. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-ПорецкогоПостроим таблицу покрытия:
22. Таблица покрытия
23. Таблица покрытия
24. Пример 3Дана СДНФ вида:Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.
25. Метод Блейка-ПорецкогоП. 1.
26. Метод Блейка-ПорецкогоП. 1.
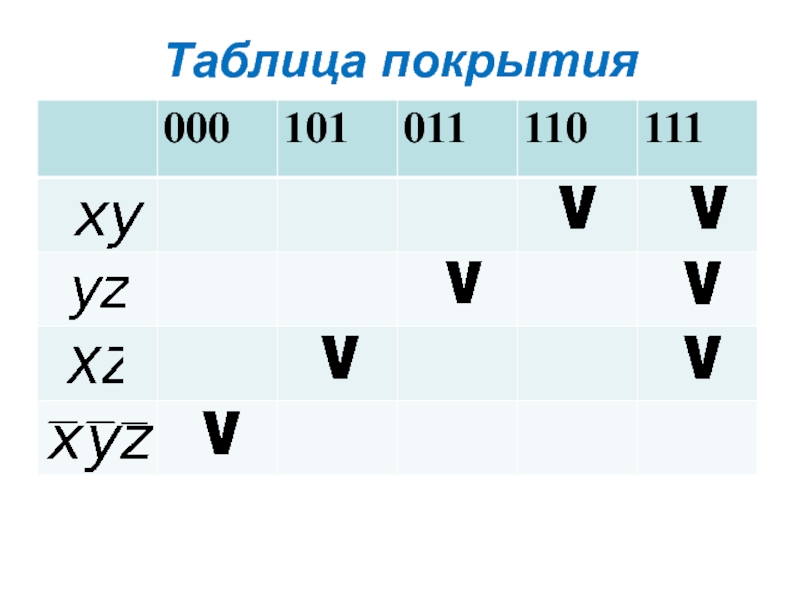
27. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-ПорецкогоПостроим таблицу покрытия:
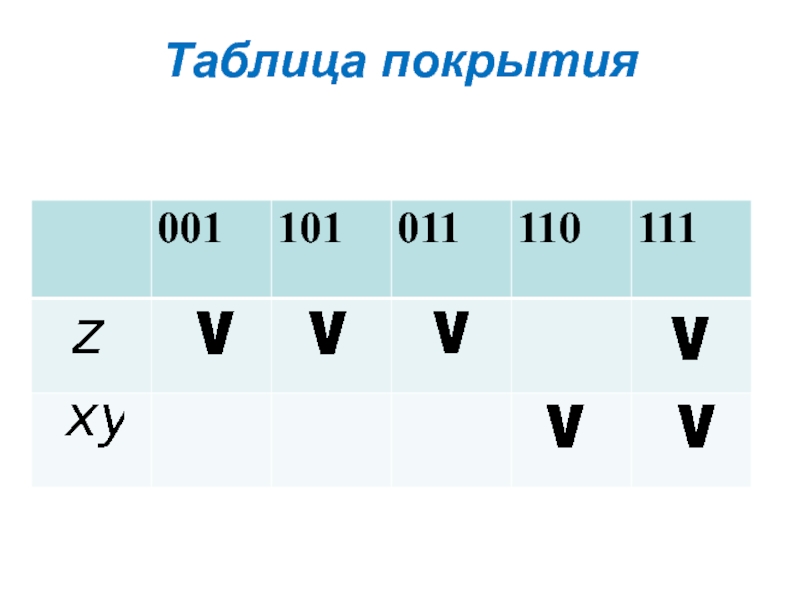
28. Таблица покрытия
29. Таблица покрытия
30. Скачать презентанцию

Тупиковая ДНФОтношение покрытия между единичными наборами и импликантами ДНФ наглядно задается таблицей покрытия.

Главная
Разное
Дискретная математика

Слайды и текст этой презентации

Слайд 1Дискретная математика

Дискретная математика

Слайд 2Тупиковая ДНФ

Отношение покрытия между единичными наборами и импликантами ДНФ наглядно

задается таблицей покрытия.

Тупиковая ДНФОтношение покрытия между единичными наборами и импликантами ДНФ наглядно задается таблицей покрытия.

Слайд 3Таблица покрытия
Строки таблицы соответствуют конъюнкциям ДНФ, столбцы – элементам единичного

множества. На пересечении строки и столбца ставится пометка, если данная

конъюнкция обращается в единицу данным набором значений аргументов (набор покрывается единичным множеством конъюнкции).

Таблица покрытияСтроки таблицы соответствуют конъюнкциям ДНФ, столбцы – элементам единичного множества. На пересечении строки и столбца ставится

Слайд 4Пример
Пусть ДНФ функции имеет вид:

Тогда ее единичное множество может быть

представлено в виде:

Построим таблицу покрытия.

ПримерПусть ДНФ функции имеет вид:Тогда ее единичное множество может быть представлено в виде:Построим таблицу покрытия.

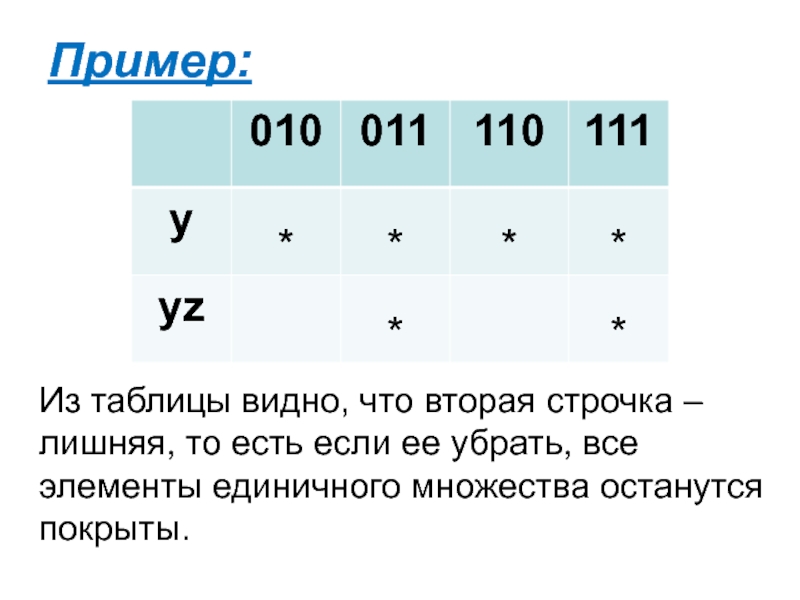
Слайд 5Пример:
Из таблицы видно, что вторая строчка – лишняя, то есть

если ее убрать, все элементы единичного множества останутся покрыты.

Пример:Из таблицы видно, что вторая строчка – лишняя, то есть если ее убрать, все элементы единичного множества

Слайд 6Значит, импликант yz – лишний импликант.
Пример
Таким образом, ДНФ можно упростить,

убрав лишний импликант.
Эта ДНФ является тупиковой, так как оставшийся импликант

– простой.

Так бывает не всегда.

Значит, импликант yz – лишний импликант.ПримерТаким образом, ДНФ можно упростить, убрав лишний импликант.Эта ДНФ является тупиковой, так

Слайд 7Тупиковая ДНФ
Сокращенная ДНФ, из которой удалены все лишние импликанты,

называется тупиковой.

Тупиковая ДНФ Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой.

Слайд 8Замечание 1
Чтобы с помощью таблицы покрытия получить тупиковую ДНФ, необходимо

сначала получить сокращенную ДНФ (скрДНФ) и именно ее простые импликанты

помещать в таблицу покрытия.

Замечание 1Чтобы с помощью таблицы покрытия получить тупиковую ДНФ, необходимо сначала получить сокращенную ДНФ (скрДНФ) и именно

Слайд 9Замечание 2
У функции может быть несколько тупиковых ДНФ. Чтобы найти

их необходимо построить сокращенную ДНФ, содержащую все простые импликанты данной

функции.

Замечание 2У функции может быть несколько тупиковых ДНФ. Чтобы найти их необходимо построить сокращенную ДНФ, содержащую все

Слайд 10Метод Блейка-Порецкого –
метод получения сокращенной ДНФ, содержащей все простые импликанты.
Пусть

дана СДНФ функции.

1. Перенумеруем элементарные конъюнкции.
2. Осуществим попарно склеивание

каждой конъюнкции с каждой, если это возможно. Под полученными конъюнкциями будем фиксировать номера.

Метод Блейка-Порецкого –метод получения сокращенной ДНФ, содержащей все простые импликанты.Пусть дана СДНФ функции.1. Перенумеруем элементарные конъюнкции. 2.

Слайд 11Метод Блейка-Порецкого
3. Допишем к списку полученных конъюнкций те, которые не

участвовали в склеивании (их номера не фиксировались).
4. Вернемся к

п.1.

В результате получим сокращенную ДНФ, содержащую все простые импликанты.

Метод Блейка-Порецкого3. Допишем к списку полученных конъюнкций те, которые не участвовали в склеивании (их номера не фиксировались).

Слайд 12Пример 1
Дана СДНФ вида:
Получить с помощью метода Блейка-Порецкого сокращенную ДНФ,

содержащую все простые импликанты.

Пример 1Дана СДНФ вида:Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.

Слайд 13Метод Блейка-Порецкого
П. 1.

;

П. 2, 3. ;

П.4 .

Метод Блейка-ПорецкогоП. 1.

Слайд 14Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид:

Метод Блейка-Порецкого
Построим таблицу покрытия:

Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-ПорецкогоПостроим таблицу покрытия:

Слайд 15Таблица покрытия

Таблица покрытия

Слайд 16Таблица покрытия

Таблица покрытия

Слайд 17Таблица покрытия

Таблица покрытия

Слайд 18Таблица покрытия

Таблица покрытия

Слайд 19Пример 2
Дана СДНФ вида:
Получить с помощью метода Блейка-Порецкого сокращенную ДНФ,

содержащую все простые импликанты.

Пример 2Дана СДНФ вида:Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.

Слайд 20Метод Блейка-Порецкого
П. 1.

П. 2, 3.

П.4.

Метод Блейка-ПорецкогоП. 1.

Слайд 21Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид:

Метод Блейка-Порецкого
Построим таблицу покрытия:

Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-ПорецкогоПостроим таблицу покрытия:

Слайд 22Таблица покрытия

Таблица покрытия

Слайд 23Таблица покрытия

Таблица покрытия

Слайд 24Пример 3
Дана СДНФ вида:
Получить с помощью метода Блейка-Порецкого сокращенную ДНФ,

содержащую все простые импликанты.

Пример 3Дана СДНФ вида:Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.

Слайд 25Метод Блейка-Порецкого
П. 1.

П. 2, 3.

П.4. l

Метод Блейка-ПорецкогоП. 1.

Слайд 26Метод Блейка-Порецкого
П. 1.

П. 2, 3.

П.4. l

Метод Блейка-ПорецкогоП. 1.

Слайд 27Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид:

Метод Блейка-Порецкого
Построим таблицу покрытия:

Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-ПорецкогоПостроим таблицу покрытия:

Слайд 28Таблица покрытия

Таблица покрытия

Слайд 29Таблица покрытия

Таблица покрытия

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей