Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дискретная математика
Содержание
- 1. Дискретная математика
- 2. СвязностьПусть G =(V, E) – н-граф.Связными называются
- 3. СвязностьУтверждение: отношение связности является отношением эквивалентности.Доказательство:1.Каждая вершина
- 4. Связность2. Если вершина a связна с b,
- 5. Связность3. Если вершина a связана маршрутом с
- 6. СвязностьОтношение рефлексивно, симметрично и транзитивно, значит является
- 7. СвязностьСвязными компонентами графа G называются подграфы, порожденные
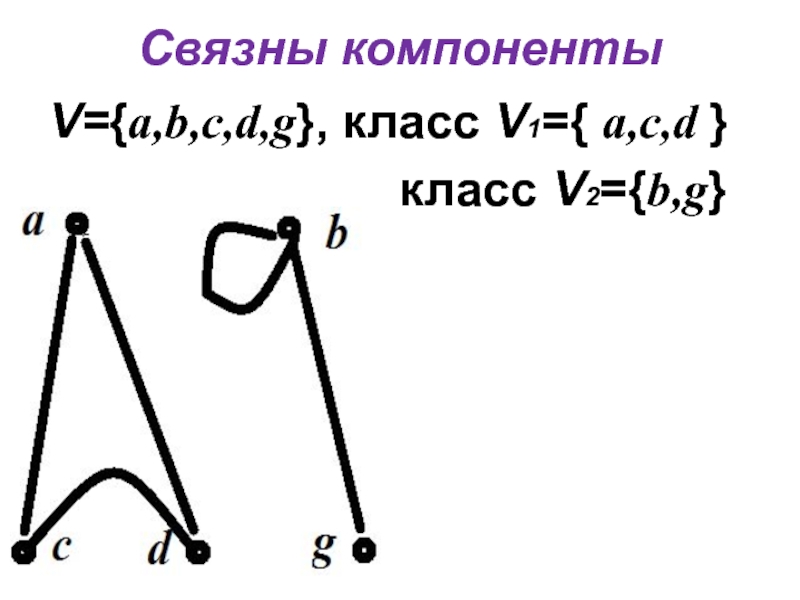
- 8. Связны компонентыV={a,b,c,d,g}, класс V1={ a,c,d }
- 9. Разделяющие множестваРазделяющим множеством н-графа G =(V, E)
- 10. Разделяющие множестваРазрезом в н-графе G =(V, E)
- 11. Разделяющие множестваМостом или перешейком в н-графе G =(V, E) называется разрез, состоящий из одного ребра.
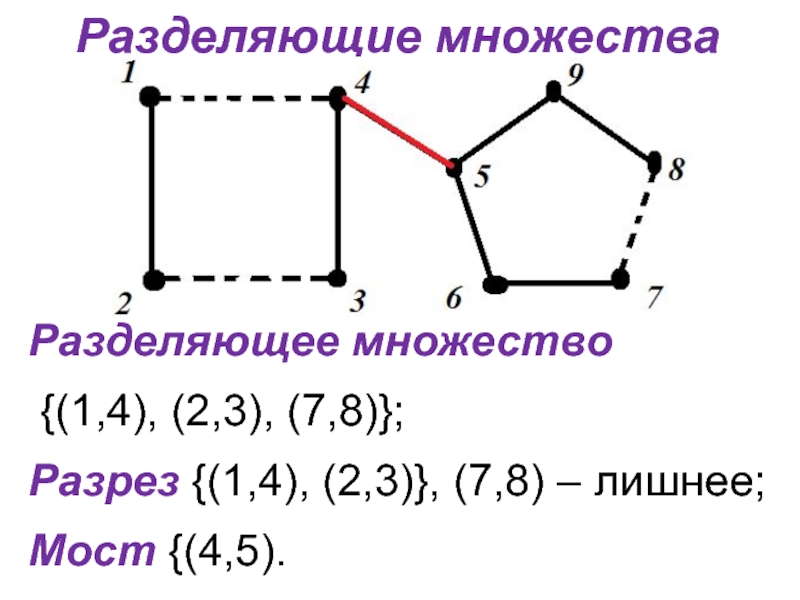
- 12. Разделяющие множестваРазделяющее множество {(1,4), (2,3), (7,8)};Разрез {(1,4), (2,3)}, (7,8) – лишнее;Мост {(4,5).
- 13. ШарнирВершина - н-графа G
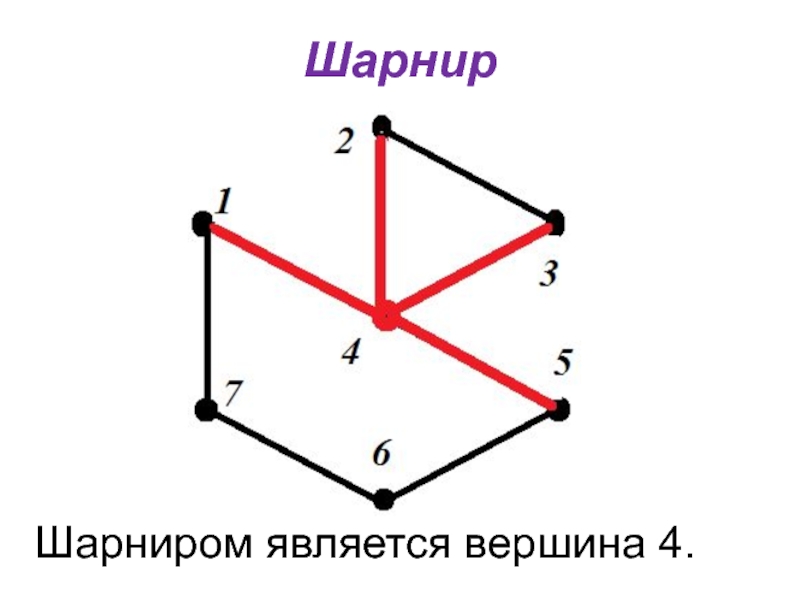
- 14. ШарнирШарниром является вершина 4.
- 15. Скачать презентанцию
СвязностьПусть G =(V, E) – н-граф.Связными называются вершины a и b если существуют маршрут, связывающий их.Н-граф G называется связным, если все его вершины связны
Слайды и текст этой презентации
Слайд 2Связность
Пусть G =(V, E) – н-граф.
Связными называются вершины a и
b если существуют маршрут, связывающий их.
все его вершины связны
Слайд 3Связность
Утверждение: отношение связности является отношением эквивалентности.
Доказательство:
1.Каждая вершина связана сама с
собой маршрутом нулевой длины, значит отношение связости рефлексивно.
Слайд 4Связность
2. Если вершина a связна с b, то и b
связна с a. Если a с b связаны маршрутом М(a,b),
то b с a связаны маршрутом М(b,a), где ребра и вершины идут в обратном порядке. Значит отношение связости симметрично.
Слайд 5Связность
3. Если вершина a связана маршрутом с b, b связана
с с, то и a связана маршрутом с с. Это
маршрут, начало которого М(a,b), окончание – M(b,c), вершина b – общая.Значит отношение связости транзитивно.
Слайд 6Связность
Отношение рефлексивно, симметрично и транзитивно, значит является отношением эквивалентности.
Множество вершин
V разбивается отношением связности на классы эквивалентности – подмножества связных
вершин.
Слайд 7Связность
Связными компонентами графа G называются подграфы, порожденные классами эквивалентности по
отношению связности.
Замечание: В связном графе одна связная компонента.
Слайд 9Разделяющие множества
Разделяющим множеством
н-графа G =(V, E) называется множество ребер,
при удалении которых число компонент связности графа увеличивается.
Слайд 10Разделяющие множества
Разрезом в н-графе G =(V, E) называется разделяющее множество
в котором нет лишних ребер, то есть минимальное разделяющее множество.
Слайд 11Разделяющие множества
Мостом или перешейком
в н-графе G =(V, E)
называется разрез, состоящий из одного ребра.
Слайд 12Разделяющие множества
Разделяющее множество
{(1,4), (2,3), (7,8)};
Разрез {(1,4), (2,3)}, (7,8) –
лишнее;
Мост {(4,5).
Слайд 13Шарнир
Вершина - н-графа G =(V, E) называется
шарниром, если удаление этой вершины и всех инцидентных ей ребер
приводит к увеличению числа компонент связности графа.
