Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисциплина МАТЕМАТИКА
Содержание
- 1. Дисциплина МАТЕМАТИКА
- 2. Балльно-рейтинговая система 1 курсОн-лайн 1 лекции 5
- 3. 3.Учебный вопрос. Метод Гаусса систем линейных алгебраических уравнений.
- 4. Карл Фридрих Гаусс (30.04.1777-23.02.1855) Немецкий математик, механик,
- 5. Рассмотрим систему m линейных алгебраических уравнений с
- 6. Напомним, элементарными преобра-зованиями строк матрицы называются:1) перемена
- 7. Напомним, рангом матрицы размерности m×n называется
- 8. Определение. Две системы линейных алгебраических уравнений называются
- 9. Метод Гаусса. В отличие от матричного метода и
- 10. Алгоритм решения систем линейных уравнений методом Гаусса .
- 11. 1)Расширенную матрицу системы с помощью элементарных преобразований
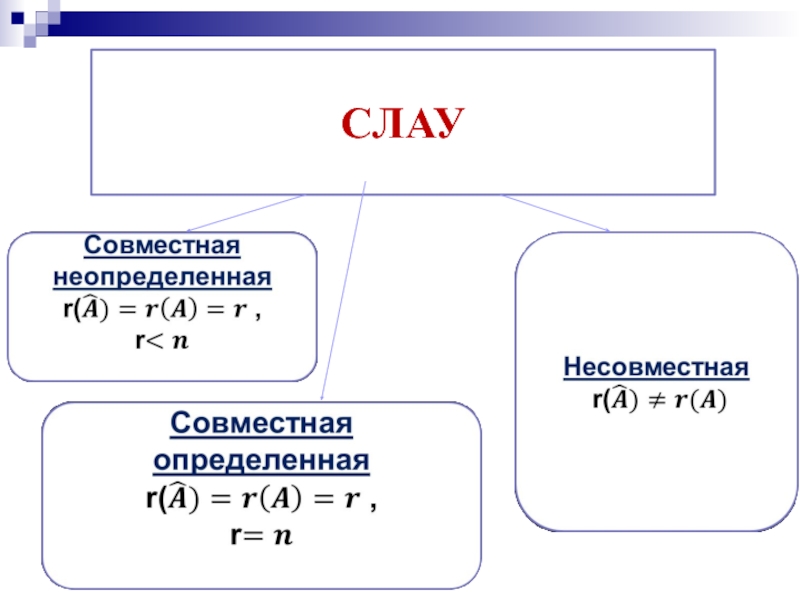
- 12. СЛАУ
- 13. Если система имеет единственное решение, то, двигаясь
- 14. 4) Неизвестная, соответствующая столбцу, в котором стоит
- 15. Пример. Решить систему методом Гаусса.Решение. –2 –1 –2 3 + +
- 16. + 1/5
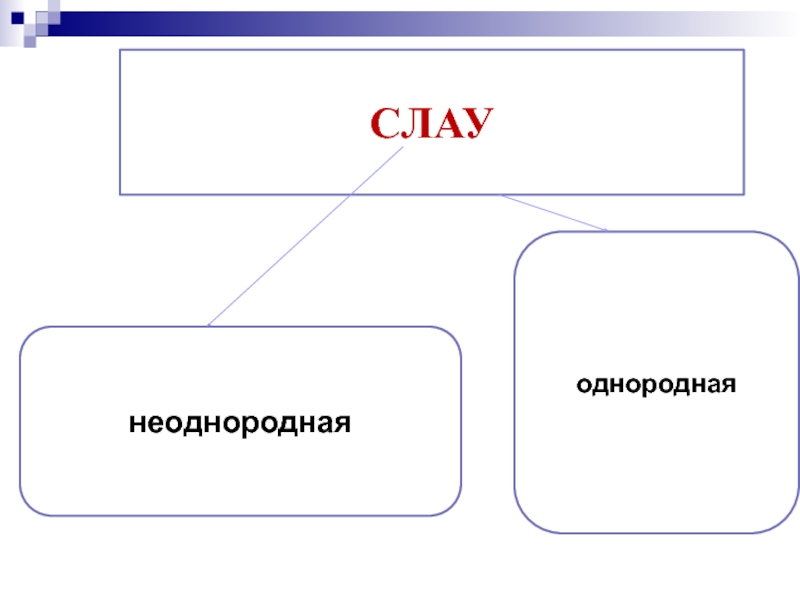
- 17. однороднаянеоднороднаяСЛАУ
- 18. Система линейных алгебраических уравнений называется однородной СЛАУ,
- 19. Очевидно, что x1=x2=…=xn=0 – нулевое или тривиальное
- 20. Задание на самостоятельную работу (ППИ, 1
- 21. Скачать презентанцию
Балльно-рейтинговая система 1 курсОн-лайн 1 лекции 5 баллов (max 1*5=5); 3 лаб. занятия по 5 баллов(max 3*5=15); Контрольная работа №1 задачи 1,3а,б.в,8
Слайды и текст этой презентации
Слайд 1Дисциплина МАТЕМАТИКА
Лектор: Юлия Абдулловна Ахкамова,
доцент кафедры математики и методики обучения математике ЮУрГГПУ
Слайд 2Балльно-рейтинговая система 1 курс
Он-лайн 1 лекции 5 баллов (max 1*5=5);
3
лаб. занятия по 5 баллов(max 3*5=15); Контрольная работа №1 задачи 1,3а,б.в,8 (max 60);
Защита-обсуждение занятий или кр (электронного варианта) max 10 баллов);
Зачетная работа до 20 баллов .
60 баллов и выше «Зачтено»,
Слайд 4Карл Фридрих Гаусс (30.04.1777-23.02.1855)
Немецкий математик, механик, физик, астроном и
геодезист. Считается одним из величайших математиков всех времён, «королём математиков».
Иностранный член Шведской
и Российской Академий
наук, английского
Королевского общества.
Слайд 5Рассмотрим систему m линейных алгебраических уравнений с n неизвестными. Расширенной
матрицей системы называется основная матрица с приписанным справа столбцом свободных
членов:
Слайд 6Напомним, элементарными преобра-зованиями строк матрицы называются:
1) перемена местами двух строк
матрицы;
2) умножение строки на любое ненулевое число;
3) прибавление к элементам
одной строки соответствующих элементов другой строки, умноженных на некоторое число;4) вычеркивание нулевой строки.
Слайд 7Напомним, рангом матрицы размерности m×n называется количество ненулевых строк
в эквивалентной ей ступенчатой матрице.
Ступенчатая матрица получена из
исходной с помощью элементарных преобразований строк.
Слайд 8Определение. Две системы линейных алгебраических уравнений называются эквивалентными или равносильными,
если они имеют одно и то же множество решений.
Слайд 9Метод Гаусса.
В отличие от матричного метода и метода Крамера метод
Гаусса может быть применен к СЛАУ с произвольным числом уравнений
и неизвестных.Суть метода Гаусса заключается в последовательном исключении неизвестных.
Слайд 111)Расширенную матрицу системы с помощью элементарных преобразований приводим к ступенчатому
виду.
2)Отбрасываем нулевые строки.
3) Применяем следующую теорему:
Теорема Кронеккера-Капелли:
При совпадении рангов
расширенной и основной матриц СЛАУ совместна; при равенстве ранга с числом неизвестных СЛАУ определена.
Слайд 13
Если система имеет единственное решение, то, двигаясь по системе снизу
вверх, последовательно находим значения неизвестных.
Если система имеет бесконечное множество решений,
то сначала выделяем базисные неизвестные. 
Слайд 144) Неизвестная, соответствующая столбцу, в котором стоит первый ненулевой элемент
данной строки, является базисной. Остальные неизвестные – свободные.
5) Двигаясь по
системе снизу вверх, последовательно выражаем базисные неизвестные через свободные.
Слайд 18Система линейных алгебраических уравнений называется однородной СЛАУ, если свободный член
в каждом уравнении равен нулю.
Пример. однородной системы линейных уравнений
Однородная
система всегда совместна.
Слайд 19Очевидно, что x1=x2=…=xn=0 – нулевое или тривиальное решение однородной системы.
Кроме тривиального, система может иметь и другие решения (нетривиальные).
Слайд 20Задание на самостоятельную
работу (ППИ, 1 курс)
Данко П.Е., др. Высшая
математика в упражнениях и задачах, часть I, с.39-43, 70-79.
Контрольная
работа №1 задания 1;(3а,3б);3в;8.
